Managerial Economics 1.3: Partial Derivatives
TLDRIn this final video of the math review series, Sebastian Y delves into the concept of partial derivatives and their role in maximizing multivariate functions, which are crucial for understanding complex economic systems with multiple decision variables. He explains that partial derivatives follow the same rules as regular derivatives but are taken with respect to a single variable while treating others as constants. Using two examples, one involving economic agents with interdependent decisions and the other focusing on a single decision-maker with multiple choices, he illustrates how to set up and solve systems of equations derived from first-order conditions. The video also touches on the application of partial derivatives in game theory and constrained optimization problems, providing a solid foundation for further study in managerial economics.
Takeaways
- 📚 Partial derivatives are used to optimize multivariate functions, which are common in complex economic systems with multiple decision variables or interdependent decision-makers.
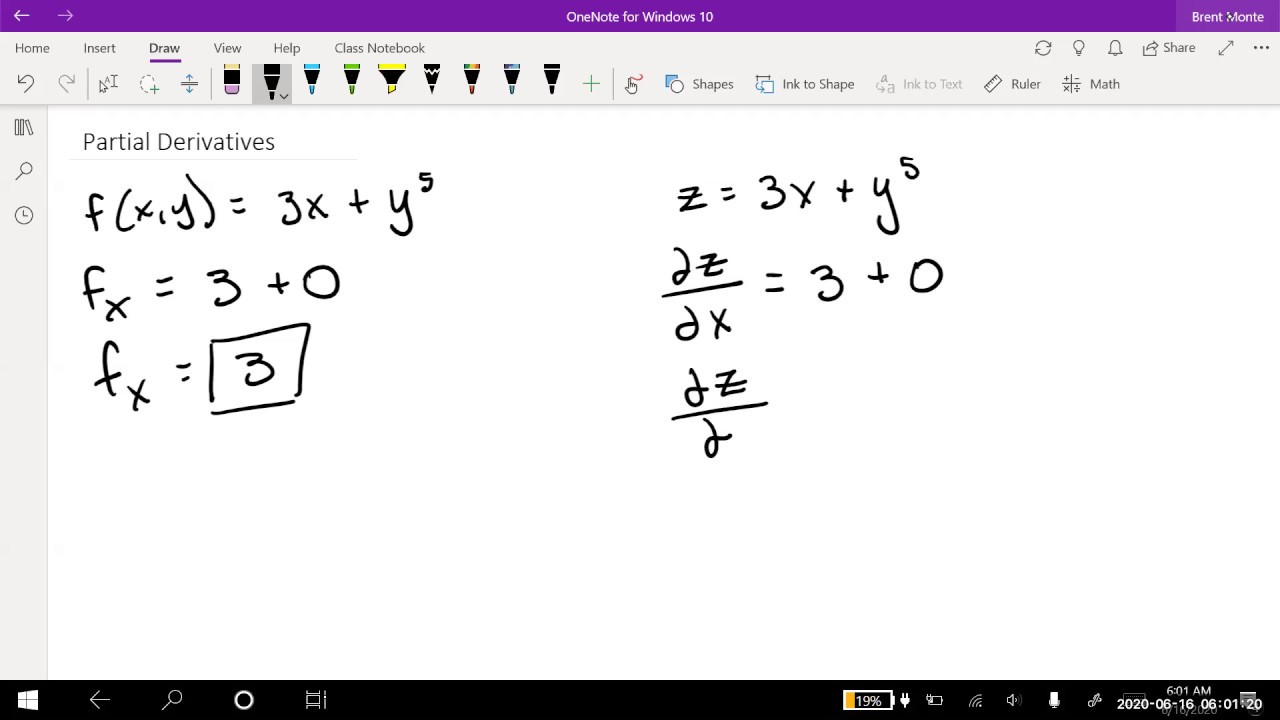
- 🔍 When taking a partial derivative, treat all other variables as constants, applying the same derivative rules as with regular constants.
- 🧐 Economic agents' decisions can affect each other, and their objective functions (f1, f2, etc.) can be interdependent, requiring the use of partial derivatives to find optimal decisions.
- 📝 The first order condition (FOC) for optimization is found by setting the partial derivative of the objective function equal to zero for each decision variable.
- 🔑 Leibniz notation uses a curly 'd' to denote partial derivatives, distinguishing them from regular derivatives.
- 🤝 Solving FOCs involves setting up and solving a system of equations, which can be done through various methods, including substitution.
- 🔢 In the provided example, agent 1's decision variable x1 is solved in terms of agent 2's decision variable x2, and vice versa, leading to the optimal values for both variables.
- 🎯 The process demonstrated is foundational to game theory problems, where multiple agents' decisions are interdependent.
- 🛍️ Real-world applications of partial derivatives include consumer choice theory, cost minimization, and other multivariate optimization problems.
- ⛓️ Constrained optimization problems, where decision-makers face restrictions, are also a focus, but the script focuses on unconstrained optimization for simplicity.
- 📈 The objective function in the second example involves maximizing a function of two variables, x1 and x2, using partial derivatives to find the optimal values.
- 📊 Second-order derivatives can be used to confirm whether a point is a maximum or minimum, but this is not covered in the class and it's assumed that the function behaves as expected.
Q & A
What is the main topic of this video?
-The main topic of this video is the discussion of partial derivatives and how to maximize multivariate functions in the context of managerial economics.
Why are partial derivatives important in the study of economic systems?
-Partial derivatives are important because they allow for the optimization of objective functions in complex economic systems that have more than one choice variable or involve multiple decision-makers whose decisions impact each other.
How do partial derivatives differ from regular derivatives?
-Partial derivatives differ from regular derivatives in that they are taken with respect to a certain variable while treating all other variables as constants, as opposed to considering all variables as potentially changing.
What is the first order condition (FOC) for agent one in the given example?
-The first order condition for agent one (FOC1) is the partial derivative of the objective function f1 with respect to x1, treating x2 as a constant.
What is the process for solving a system of equations with two choice variables?
-The process involves taking the partial derivatives of the objective functions with respect to each choice variable, setting up the first order conditions, and solving them simultaneously as a system of equations to find the optimal values for both variables.
How did the video solve for x1 and x2 in the first example with two economic agents?
-The video solved for x1 and x2 by first solving the first order condition for x1 to express it in terms of x2, then substituting this expression into the second order condition to solve for x2, and finally substituting the value of x2 back into the expression for x1.
What is the objective function in the second example of unconstrained optimization?
-The objective function in the second example is x1x2 + x1 + x2 - x1^2 - x2^2, where x1 and x2 are the choice variables that need to be optimized.
What are the first order conditions for the second example with the objective function f of x1 and x2?
-The first order conditions are the partial derivatives of the objective function with respect to x1 and x2, which are set to zero to find the optimal values of x1 and x2.
How does the video handle the system of equations resulting from the first order conditions in the second example?
-The video solves the system of equations by first solving one of the equations for one variable, then substituting this into the other equation to solve for the remaining variable, and finally using the value found to determine the value of the first variable.
What is the final solution for x1 and x2 in the second example of unconstrained optimization?
-The final solution for x1 and x2 in the second example is x1 = 1 and x2 = 1, which are the values that maximize the given objective function.
Why is it important to be careful with the distributive property when solving systems of equations?
-It is important to be careful with the distributive property because incorrect application can lead to mistakes in solving the system of equations, which is a common error and a leading cause of points lost in homework assignments in the course.
Outlines
📚 Introduction to Partial Derivatives in Managerial Economics
Sebastian Y introduces the concept of partial derivatives and their application in optimizing multivariate functions within complex economic systems. He explains that partial derivatives are similar to regular derivatives but are taken with respect to a specific variable while treating others as constants. Using an example with two economic agents making decisions (agent one with objective function f1 and agent two with f2), he demonstrates how to calculate first order conditions (FOCs) for each agent's decision variable. The FOCs are then solved as a system of equations to find the optimal values for both agents' decisions.
🧮 Solving a System of Equations in Game Theory
The video continues with a detailed example of solving a system of equations, which turns out to be the first problem in game theory. It involves finding the optimal values for two decision variables, x1 and x2. The process includes taking partial derivatives of an objective function with respect to each variable, treating the other variable as a constant. The resulting first order conditions are then solved simultaneously to find the values of x1 and x2 that maximize the objective function. The example serves as a practical exercise in using partial derivatives and solving systems of equations.
🔍 Unconstrained Optimization and Common Mistakes
Sebastian Y discusses unconstrained optimization, where a single decision maker has multiple decisions to make simultaneously. He uses an objective function f of x1 and x2 to illustrate the process of finding the optimizing values for these variables. The video emphasizes the importance of correctly taking partial derivatives and setting up the first order conditions. A common mistake, specifically the incorrect distribution of terms, is highlighted to ensure that viewers are careful during their calculations. The video concludes with the solution to the system of equations, finding the maximizing values for x1 and x2, and a brief mention of second derivatives for verifying maxima or minima, although it is noted that this will not be covered in the class.
Mindmap
Keywords
💡Partial Derivatives
💡Multivariate Functions
💡First Order Conditions (FOC)
💡Optimization
💡Leibniz Notation
💡System of Equations
💡Objective Function
💡Decision Makers
💡Unconstrained Optimization
💡Game Theory
💡Consumer Choice
Highlights
Partial derivatives are introduced as a tool for optimizing multivariate functions in complex economic systems.
Economic systems can be complex due to multiple decision variables or interdependent decision makers.
Partial derivatives follow the same rules as regular derivatives but are taken with respect to a single variable while treating others as constants.
The concept of treating other variables as constants is crucial for understanding partial derivatives.
An example is provided with two economic agents, each with an objective function influenced by the decisions of the other.
Objective functions f1 and f2 are defined with respect to decisions x1 and x2 made by agents 1 and 2 respectively.
First order conditions (FOCs) for each agent are derived using partial derivatives.
Leibniz notation with a curly d is used to denote partial derivatives clearly.
The process of solving FOCs for multiple variables involves solving a system of equations.
Substitution is used to solve the system of FOCs for the example given.
The solution to the system of FOCs provides the optimal values for both decision variables x1 and x2.
The video presents the first application of game theory by solving a problem with simultaneous decision making.
Partial derivatives are also essential for a single decision maker with multiple decisions to make at once.
Examples include consumer choice and cost minimization problems, which are multivariate optimizations.
The video covers an unconstrained optimization problem for practice with partial derivatives.
An objective function with two choice variables is maximized using partial derivatives.
First order conditions are set up for both choice variables and solved as a system of equations.
Careful application of the distributive property is emphasized to avoid common mistakes.
The final values for the choice variables are found, demonstrating the optimization process.
The video concludes the math review section, preparing viewers for further study in managerial economics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: