The Fundamental Theorem of Calculus - Proof
TLDRThe video presents a detailed sketch of the proof for the Fundamental Theorem of Calculus, starting with a positive and continuous function f(x) on the XY plane. An area function, A(x), is constructed to represent the area under the curve from a constant point 'a' to a variable point 'x'. By using a geometric argument, the video demonstrates that A(x) is an antiderivative of f(x), denoted as A'(x) = f(x). The proof leverages the uniqueness of antiderivatives up to a constant, which is determined by setting x to 'a', revealing the constant C as the negative of f(a). Ultimately, the video derives the well-known form of the Fundamental Theorem of Calculus, which connects the definite integral from 'a' to 'b' of f(t)dt with the antiderivative F(x) at points 'a' and 'b', expressed as F(b) - F(a). The elegance of the proof lies in its simplicity and the geometric intuition it employs to establish a foundational concept in calculus.
Takeaways
- 📈 The fundamental theorem of calculus connects the concept of definite integrals and anti-derivatives, showing that the definite integral of a function can be represented as the difference of its anti-derivatives.
- 🎯 The area function, denoted by uppercase A(X), is defined as the area under the curve of the function f(X) from a constant value 'a' to a variable value 'X'.
- 🔍 The process involves choosing a dummy variable (T, U, V) for integration to avoid confusion with the variable of integration 'X'.
- 🧩 The key insight is that anti-derivatives are unique up to a constant, meaning that any two anti-derivatives of a function differ by a constant.
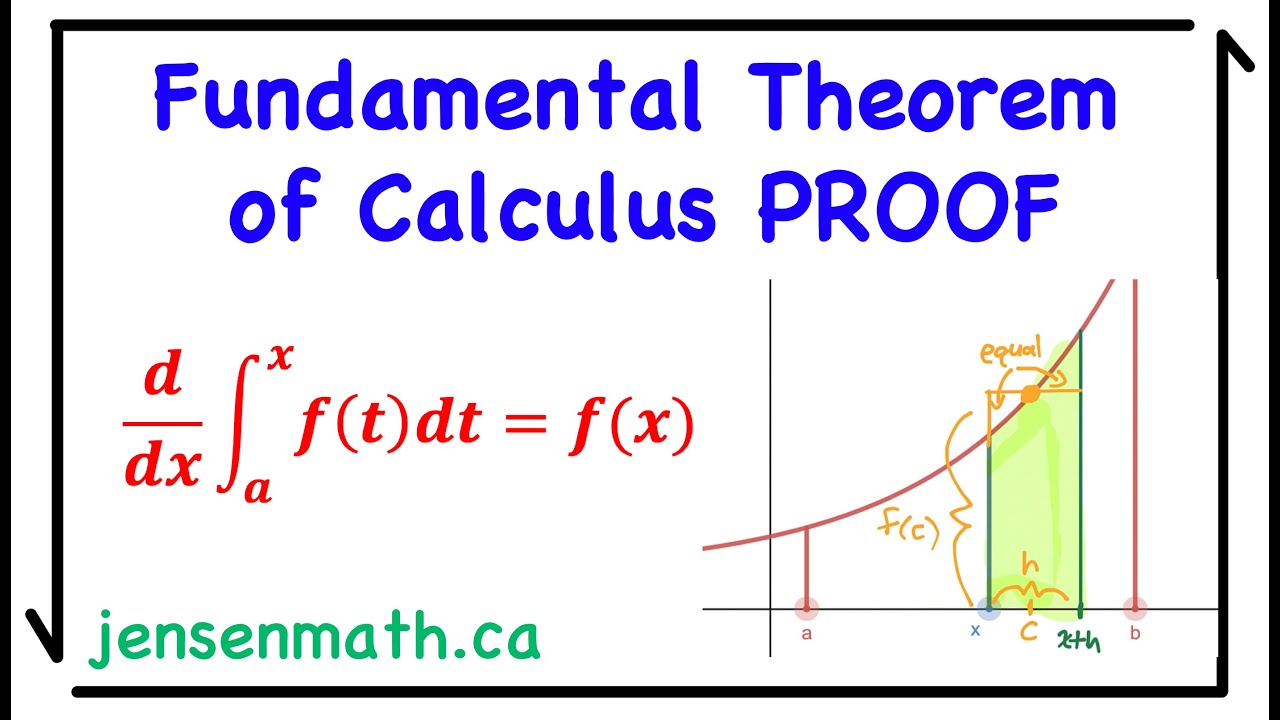
- 📐 To prove that the area function is an anti-derivative of f(X), the derivative of the area function is taken, using the limit definition of the derivative as H approaches zero.
- 🔵 The geometric argument involves finding a rectangle whose area exactly matches the area under the curve f(X) between X and X+H, leading to the identification of a 'sweet spot', denoted as X-hat.
- 🔸 The height of the rectangle that matches the area under the curve is f(X-hat), and the width is H, leading to the simplification of the area function's derivative.
- 🤔 By letting H approach zero, it is shown that the limit of f(X-hat) as H approaches zero is f(X), which means the area function's derivative is indeed f(X).
- ✅ The area function, being an anti-derivative of f(X), must be of the form F(X) + C, where F(X) is an antiderivative and C is a constant.
- 🔑 To solve for the constant C, the value of X is chosen such that it simplifies the integral to zero, which in this case is when X equals 'a'.
- 🧮 The final form of the fundamental theorem of calculus is derived, showing that the integral from 'a' to 'b' of f(t)dt equals F(b) - F(a), where F is an antiderivative of f.
- 📝 The proof concludes by summarizing the geometric and algebraic steps that lead to the fundamental theorem of calculus, emphasizing the elegance and simplicity of the argument.
Q & A
What is the fundamental theorem of calculus?
-The fundamental theorem of calculus is a theorem that links the concept of differentiating a function with that of integrating a function. It states that if a function is continuous and its integral from a to b is F(b) - F(a), then the derivative of F(x) is f(x).
What is the area function in the context of the fundamental theorem of calculus?
-The area function, denoted as uppercase A of x, is a function that represents the area under the curve of f(x) from a constant value a to a variable value x. It is used to construct an anti-derivative for the function f(x).
Why is it necessary to use a different variable for integration when x is already the variable of the interval?
-A different variable, often called a dummy variable like t or u, is used for integration to avoid confusion and to maintain the clarity of the mathematical expression when x is already representing the variable of the interval.
What is the significance of the rectangle in the geometric argument of the proof?
-The rectangle is used to approximate the area under the curve f(x) between x and x+h. By finding the 'sweet spot' for the height of the rectangle (x-hat), the area of the rectangle can be made to exactly match the area under the curve, which is key to proving that the area function is an anti-derivative of f(x).
How is the derivative of the area function found?
-The derivative of the area function is found by applying the definition of the derivative, which involves taking the limit as h approaches zero of the difference quotient of the area function at x+h and x.
What is the role of continuity in the proof of the fundamental theorem of calculus?
-Continuity of the function f(x) ensures that there are no breaks in the function, allowing for the construction of a rectangle that can approximate the area under the curve without gaps or overlaps.
How is the constant C found in the anti-derivative of f(x)?
-The constant C is found by setting x equal to the constant value a, which makes the area function equal to zero since there is no interval between a and a. This allows us to solve for C as the negative of f(a).
What is the final form of the fundamental theorem of calculus?
-The final form of the fundamental theorem of calculus states that the definite integral from a to b of f(x) dx is equal to the antiderivative F(x) evaluated at b minus the antiderivative evaluated at a, i.e., F(b) - F(a).
Why is it important to show that the area function is an anti-derivative of f(x)?
-Showing that the area function is an anti-derivative of f(x) is crucial because it establishes a direct connection between the process of integration (finding areas) and differentiation (finding rates of change or slopes), which is the core of the fundamental theorem of calculus.
What does the term 'anti-derivative' mean?
-An anti-derivative, also known as an indefinite integral, is a function whose derivative is equal to the original function. The concept of anti-derivatives is central to the fundamental theorem of calculus, which shows that differentiation and integration are essentially inverse operations.
How does the proof use the concept of limits?
-The proof uses the concept of limits to find the derivative of the area function. By taking the limit as h approaches zero in the difference quotient, the relationship between the area function and the original function f(x) is established.
What is the significance of the dummy variable in the integral?
-The dummy variable, such as t or u, is used in the integral to represent the variable of integration without causing confusion with the variable representing the limits of integration, which in this case is x.
Outlines
📐 Introduction to the Fundamental Theorem of Calculus
This paragraph introduces the concept of sketching the proof of the Fundamental Theorem of Calculus. It begins by visualizing the graph of a positive and continuous function f(x) in the XY plane. The focus is on constructing an area function, uppercase A(x), which represents the area under the curve of f(x) from a constant value 'a' to a variable value of 'x'. The definite integral is then used to express the area under the curve, with a different variable 'T' used as the dummy variable for integration to avoid confusion with 'x'. The paragraph also introduces the indefinite integral of f(x) and emphasizes the uniqueness of anti-derivatives up to a constant, which is pivotal for the argument.
📏 Deriving the Area Function as an Anti-derivative
The second paragraph delves into the process of proving that the area function is an anti-derivative of f(x). It begins by defining the area function at x + h and then subtracting the area function at x, which leads to the area of the second piece. The goal is to find a rectangle whose area equals the area under the curve f between x and x + h. The continuity of f is leveraged to find a 'sweet point', denoted as x-hat, where the area of the rectangle matches the area under f. The height of the rectangle is f(x-hat), and the width is h. This leads to the conclusion that the derivative of the area function is f(x), thus proving it to be an anti-derivative of f(x). The paragraph concludes with the assertion that the area function must be of the form F(x) plus a constant, which is a direct consequence of the uniqueness of anti-derivatives.
🔍 Solving for the Constant in the Area Function
The final paragraph focuses on solving for the constant in the area function. It starts by expressing the area function in terms of the definite integral and then seeks a value of x that simplifies the equation, allowing for the solution of the constant 'C'. The choice of x being equal to 'a' leads to a trivial case where the area is zero, thus isolating the constant 'C' as the negative of f(a). With 'C' identified, the paragraph substitutes it back into the original equality, leading to the familiar form of the Fundamental Theorem of Calculus. The theorem is then expressed with 'T' as the variable of integration, which is then replaced with 'x' to align with the standard notation. The proof is summarized as relying on the uniqueness of anti-derivatives and a geometric argument that establishes the area function as an anti-derivative of the original function.
Mindmap
Keywords
💡Fundamental Theorem of Calculus
💡Antiderivatives
💡Definite Integral
💡Continuous Function
💡Derivative
💡Rectangle Approximation
💡Limit
💡Dummy Variable
💡Area Function
💡Constant of Integration
💡Geometric Argument
Highlights
The video aims to sketch the proof of the Fundamental Theorem of Calculus.
A new function, the area function, is constructed based on the area below the curve of the original function f(x).
The area function is defined as the definite integral of f(t) from 'a' to 'x', using 't' as a dummy variable.
The Fundamental Theorem of Calculus is introduced, connecting definite and indefinite integrals.
Anti-derivatives are unique up to the addition of a constant, which is a key point in the argument.
The area function is shown to be an anti-derivative of f(x) by finding its derivative.
The limit definition of the derivative is used to find the change in area as 'h' approaches zero.
A rectangle's area is used as an approximation for the area under the curve, leading to the discovery of the 'sweet point'.
The height of the rectangle is identified as f(x) at the point x-hat, which is the key to the area approximation.
The area of the rectangle is simplified to f(x) times the change in x, leading to the limit as 'h' approaches zero.
The limit of f(x-hat) as 'h' approaches zero converges to f(x), proving the derivative of the area function is f(x).
The area function is identified as an anti-derivative of f(x), which must be of the form F(x) plus a constant.
The constant 'C' is solved for by setting 'x' equal to 'a', resulting in the area function being F(x) - f(a).
The Fundamental Theorem of Calculus is derived in terms of the definite integral from 'a' to 'b' of f(t)dt.
The proof concludes by summarizing the two essential facts: the uniqueness of anti-derivatives and the geometric argument for the area function.
The final form of the Fundamental Theorem of Calculus is presented, relating the definite integral to the anti-derivatives at points 'a' and 'b'.
The proof is appreciated for its simplicity and elegance in demonstrating the foundational theorem of calculus.
Transcripts
Browse More Related Video

Fundamental theorem of calculus (Part 2) | AP Calculus AB | Khan Academy

Proof of fundamental theorem of calculus | AP Calculus AB | Khan Academy
1st Fundamental Theorem of Calculus PROOF | Calculus 1 | jensenmath.ca

Why Are Slope and Area Opposite: The Fundamental Theorem of Calculus
Fundamental Theorem of Calculus II

An Intuitive Understanding of the Fundamental Theorem of Calculus
5.0 / 5 (0 votes)
Thanks for rating: