Arithmetic Series (Precalculus - College Algebra 70)

Professor Leonard
19 Nov 202015:11
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a concise and straightforward approach to understanding and calculating the sum of a partial arithmetic series. It emphasizes the predictability of arithmetic series due to their uniform common difference and provides a clear method for finding the sum by knowing the first and last terms, and the number of terms. The script includes examples to illustrate the process and also touches on series notation and its application in various scenarios, ultimately demonstrating the elegance and logic behind arithmetic series and their sums.

Takeaways
  • 📚 Arithmetic series involve the addition of a constant difference between consecutive terms in a sequence.
  • 🔢 To find the sum of an arithmetic series, you need to know the first term, the last term, and the total number of terms.
  • 🧮 The formula for the sum of an arithmetic series is given by: (n/2) * (first term + last term), where n is the number of terms.
  • 🌟 If the last term or the number of terms is not known, you can still find the sequence and solve for the missing information.
  • 📊 The nth term of an arithmetic sequence can be found using the formula: a_n = a_1 + (n - 1) * d, where d is the common difference.
  • 🔍 You can verify an arithmetic series by plugging in values into the nth term formula and checking if the sequence holds true.
  • 📈 The sum of the first n even numbers can be found using the formula: n * (n + 1), which is derived from the arithmetic series sum formula.
  • 🤔 Factoring out constants from an arithmetic series can simplify the process of finding the sum, especially when dealing with a series of constants multiplied by a variable.
  • 🧠 Understanding the relationship between the arithmetic sequence and the series itself is crucial for applying the sum formula correctly.
  • 📝 When the series starts with a different term than the common difference, you can still represent it as a sequence and find the sum using the same principles.
  • 🔗 The sum of an arithmetic series can be proven and understood through the manipulation of algebraic expressions and series representations.
Q & A

  • What is an arithmetic series?

    -An arithmetic series is a sequence of numbers in which the difference between any two consecutive terms is constant. This constant difference is also known as the common difference of the series.

  • How do you find the sum of a finite arithmetic series?

    -To find the sum of a finite arithmetic series, you need to know the first term, the last term, and the total number of terms in the series. You can then use the formula: Sum = (n/2) * (first term + last term), where n is the number of terms.

  • What is the formula for the nth term of an arithmetic sequence?

    -The formula for the nth term of an arithmetic sequence is a_n = a_1 + (n - 1) * d, where a_n is the nth term, a_1 is the first term, n is the term number, and d is the common difference.

  • How can you determine the number of terms in an arithmetic series if you know the first term, the common difference, and the last term?

    -You can determine the number of terms (n) by using the nth term formula in reverse: n = (a_n - a_1) / d + 1, where a_n is the last term, a_1 is the first term, and d is the common difference.

  • What is the sum of the first 20 even numbers?

    -The sum of the first 20 even numbers can be found using the formula for the sum of the first n even numbers: Sum = n * (n + 1), where n is the number of terms. For the first 20 even numbers, the sum is 20 * (20 + 1) = 420.

  • How can you represent an arithmetic series in series notation?

    -An arithmetic series can be represented in series notation by starting with the first term and ending with the nth term. For example, if the series starts at 1 and ends at n, it would be written as ∑ (from k=1 to n) of the sequence formula evaluated at k.

  • What is the relationship between the sum of an arithmetic series and the sum of the first n natural numbers?

    -The sum of an arithmetic series with a common difference of 1 is equivalent to the sum of the first n natural numbers, which is given by the formula: Sum = n * (n + 1) / 2.

  • Can you factor out constants in an arithmetic series when finding the sum?

    -Yes, if there is a constant term in the arithmetic series, you can factor it out and then apply the sum formula to the remaining series of terms that do not include the constant.

  • What happens if you don't know the last term of an arithmetic series but you know the first term and the common difference?

    -If you don't know the last term, you can express the last term in terms of the first term and the common difference, and then solve for the number of terms (n) using the nth term formula. Once you have n, you can find the sum using the sum formula.

  • How does the formula for the sum of an arithmetic series relate to the formula for the sum of the first n even numbers?

    -The formula for the sum of the first n even numbers is a specific case of the arithmetic series sum formula where the first term is 2 (the first even number) and the common difference is also 2. The sum formula for even numbers is n * (n + 1), which is derived from the general arithmetic series sum formula.

  • What is the significance of the formula n(n + 1)/2 in the context of arithmetic series?

    -The formula n(n + 1)/2 is significant because it represents the sum of the first n natural numbers, which is directly related to the sum of an arithmetic series when the common difference is 1. It is a foundational formula used in various mathematical contexts, including the calculation of the sum of an arithmetic series with a common difference of 1.

Outlines
00:00
📚 Introduction to Arithmetic Series

The video begins with the speaker expressing their intent to be concise and to the point about arithmetic series. They define an arithmetic series as a sequence of numbers where the same number is added repeatedly and discuss the predictability of summing a finite number of terms in such a series. The speaker introduces the formula for finding the sum of an arithmetic series, emphasizing the need to know the first term, the last term, and the total number of terms. An example is provided to illustrate the process, and the speaker assures the audience that understanding these elements will make finding the sum straightforward.

05:02
🧩 Building and Solving Arithmetic Sequences

The speaker continues by delving into the specifics of building an arithmetic sequence and solving for the unknown term. They use an example where the first term is 60, the last term is 120, and the number of terms is 16, to demonstrate how to apply the arithmetic series formula. The speaker also explains how to find the 'n' value by using the formula for the nth term of an arithmetic sequence. They then show how to verify the arithmetic series by writing it in series notation and using the formula for the sum of an arithmetic series. The speaker emphasizes the importance of understanding the sequence to figure out the number of terms and to use the sum formula effectively.

10:04
🔢 Proving the Formula and Sum of Even Numbers

In the final paragraph, the speaker aims to prove the formula for the sum of an arithmetic series by breaking down a given series into simpler components. They show how to separate a series into a sum of constants and a sum of variables, using the example of the sum of even numbers. The speaker explains how to represent the series with a starting term, common difference, and number of terms, and then applies the formula for the sum of an arithmetic series. They also discuss the concept of factoring out constants and use this to derive the sum of any 'n' even numbers. The speaker concludes by reinforcing the idea that understanding how to find the sequence and sum of an arithmetic series is crucial for solving more complex problems in the future.

Mindmap
Keywords
💡Arithmetic series
An arithmetic series is the sum of the terms of an arithmetic sequence, where each term after the first is obtained by adding a constant difference to the previous term. In the video, the presenter emphasizes the process of calculating the sum of a finite arithmetic series using a formula that involves the series' first term, last term, and the number of terms. This is central to understanding how to efficiently sum up a sequence of numbers that increase by a fixed amount.
💡Partial sum
A partial sum refers to the sum of a specified number of terms at the beginning of a series, as opposed to the sum of an entire series which might be infinite. The video focuses on finding partial sums of arithmetic series, providing formulas and methods to calculate these sums without needing to individually sum every term, demonstrating the concept through examples.
💡Conciseness
Conciseness in the video refers to the presenter's intention to deliver information in a direct and straightforward manner, focusing on the essential details without unnecessary elaboration. This approach is aimed at making complex mathematical concepts like arithmetic series more accessible and understandable within a short period.
💡Common difference
The common difference in an arithmetic sequence is the constant value added to each term to get the next term in the sequence. In the video, the presenter discusses how knowing the common difference allows one to construct the sequence and find the sum of its terms by applying this difference repeatedly from the first term.
💡Sequence
A sequence in mathematics is an ordered list of numbers. The video transitions from discussing arithmetic sequences (ordered lists where the difference between consecutive terms is constant) to arithmetic series, illustrating how sequences are foundational in understanding the sums discussed.
💡Sum formula
The sum formula for an arithmetic series, as explained in the video, involves the first term, the last term, and the number of terms. It is typically expressed as (n/2) * (first term + last term), where 'n' is the number of terms. This formula is crucial for efficiently calculating the sum of the series without direct summation of all terms.
💡n-th term
The n-th term of a sequence is the term that appears in the nth position of the sequence. The video details how to find the n-th term of an arithmetic sequence using the formula a + (n-1)d, where 'a' is the first term and 'd' is the common difference. Understanding this concept is vital for constructing sequences and finding specific values within them.
💡Series notation
Series notation is a method of representing a series in a compact mathematical form, typically using summation symbols. The video touches on this topic by converting an arithmetic sequence into series notation, emphasizing the formal mathematical expression of the series which is essential for advanced understanding and manipulation of series.
💡Provable
In the context of the video, 'provable' refers to the ability to demonstrate or verify the correctness of a mathematical concept or formula through logical reasoning or additional examples. The presenter uses this term when explaining how the formulas for summing an arithmetic series can be proven using known mathematical principles, adding credibility and understanding to the methods shown.
💡Arithmetic sequence
An arithmetic sequence is a sequence of numbers in which the difference between consecutive terms is constant. This concept is a precursor to understanding arithmetic series as discussed in the video, where the presenter explains how these sequences lead to predictable sums when the terms are added together, thereby forming an arithmetic series.
Highlights

The video provides a straightforward approach to finding the sum of an arithmetic series.

The presenter emphasizes the importance of understanding arithmetic sequences to solve for series sums.

An arithmetic series is defined as a list of numbers where the same number is added repeatedly.

To find the sum of an arithmetic series, one needs to know the first term, the last term, and the number of terms.

The formula for the sum of an arithmetic series is demonstrated through an example with the first term as 60, last term as 120, and 16 terms.

The presenter illustrates how to build an arithmetic sequence from given information without listing all terms.

The common difference in an arithmetic sequence can be used to create a formula for the nth term.

The video shows how to solve for the number of terms (n) in a series using the last term and the common difference.

The formula for the sum of an arithmetic series is simplified to involve only the first term, last term, and the number of terms.

The presenter demonstrates the use of series notation and how it relates to the arithmetic sequence.

An example is given to show how the sum of an arithmetic series can be verified using the formula.

The video explains how to handle a series without a known ending value by using the concept of n terms.

The presenter shows how to factor out constants and simplify the formula for the sum of a series with a variable term count.

The concept of representing a series as a sequence is explored, allowing for a deeper understanding of the underlying pattern.

The video connects the formula for the sum of an arithmetic series to the sum of even numbers, providing a practical application.

The presenter demonstrates how to apply the formula to find the sum of the first 20 even numbers.

The video concludes by emphasizing the importance of understanding how to find the sequence, make the series, and find the sum of an arithmetic series.

Transcripts

Browse More Related Video

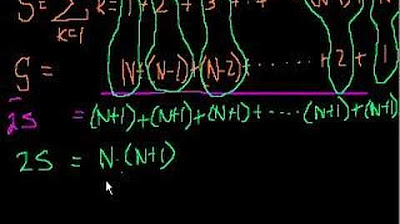
Sequences and Series (part 1)

Partial sums intro | Series | AP Calculus BC | Khan Academy

Arithmetic Sequences (Precalculus - College Algebra 69)

AP Calculus BC Lesson 10.1

Sequence and Series | Terms of Sequence and Associated Series | Pre-Calculus

Partial sums: term value from partial sum | Series | AP Calculus BC | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Arithmetic SeriesSum CalculationMathematicsEducational ContentSeries FormulaSequence CreationLogical ApproachMath TricksEducational VideoMathematical Patterns