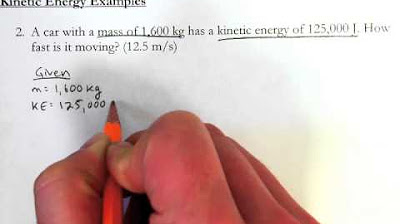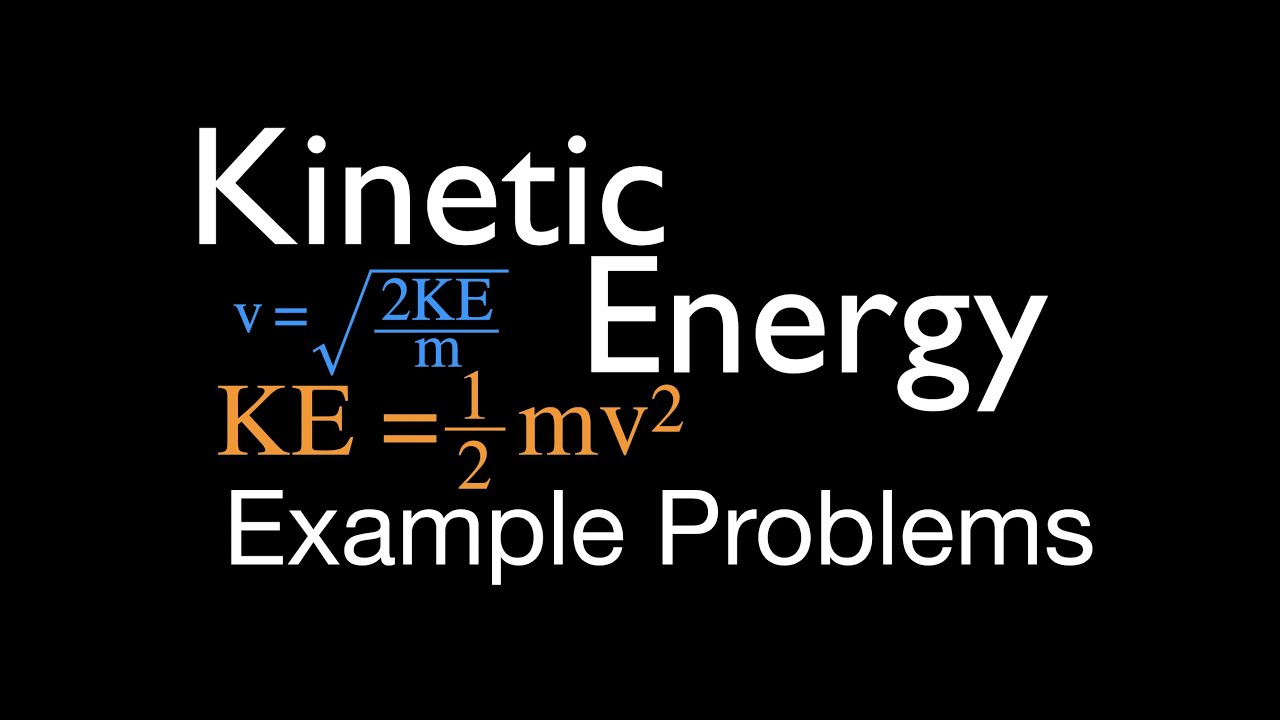Kinetic Energy Part 3 - Calculating Velocity

Science Chomp
6 Dec 201705:25
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the host explains how to calculate velocity using kinetic energy equations. The process is demonstrated with two examples: a bird with a mass of 0.25 kg and kinetic energy of 40.5 J, and a hot air balloon with a mass of 1890 kg and an enormous kinetic energy of 7655075 J. The host emphasizes the importance of using the correct formula (KE = 0.5 * m * v^2), performing the calculations step by step, and including units in the final answer to achieve full marks in physics problems.

Takeaways
  • 📚 The video is a tutorial on calculating velocity using kinetic energy equations.
  • 🎯 The formula used is KE = (1/2)mv², where KE is kinetic energy, m is mass, and v is velocity.
  • 🐦 An example given involves a bird with a mass of 0.25 kg and kinetic energy of 40.5 J.
  • 🧮 To find v², the mass is divided by twice the kinetic energy (m/(2*KE))
  • 🔢 For the bird example, dividing 0.25 kg by (2*40.5 J) results in 0.0125.
  • 🌳 The velocity (v) is found by taking the square root of v².
  • 🌬️ The bird's velocity is √324, which equals approximately 18 m/s.
  • 🎈 Another example is a hot air balloon with a mass of 1890 kg and a kinetic energy of 765,507,650 J.
  • 🧮 For the balloon, dividing 765,507,650 J by (1/2 * 1890 kg) gives v² as 81.
  • 🚀 The velocity of the balloon is √81, which equals 9 m/s.
  • 💡 The importance of including units (m/s) and completing all parts of the calculation for full marks is emphasized.
  • 📝 The tutorial encourages viewers to practice these calculations and ask questions in the comments section.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is how to calculate velocity using kinetic energy equations.

  • What is the formula used to calculate velocity from kinetic energy?

    -The formula used is V = √(KE / (1/2 * m)), where V is velocity, KE is kinetic energy, and m is mass.

  • What is the mass of the bird in the first example?

    -The mass of the bird in the first example is 0.25 kilograms.

  • What is the kinetic energy of the bird in the first example?

    -The kinetic energy of the bird in the first example is 40.5 joules.

  • What is the calculated velocity of the bird?

    -The calculated velocity of the bird is 18 meters per second.

  • What is the kinetic energy of the hot air balloon in the second example?

    -The kinetic energy of the hot air balloon in the second example is 765,507,600 joules.

  • What is the mass of the hot air balloon in the second example?

    -The mass of the hot air balloon in the second example is 1890 kilograms.

  • What is the calculated velocity of the hot air balloon?

    -The calculated velocity of the hot air balloon is 9 meters per second.

  • How many marks are awarded for each part of the calculation in the example problems?

    -Each part of the calculation, including the equation, substituting the numbers, the answer, and the unit, is worth one mark.

  • What is the importance of including units in the calculation?

    -Including units in the calculation is crucial as it ensures the accuracy and applicability of the result. For instance, in the context of the video, the velocity should be expressed in meters per second (m/s).

  • What mistake does the presenter make while writing the formula?

    -The presenter mistakenly writes 'em' instead of 'm' when referring to mass in the formula.

  • Why is it important to show all parts of the calculation?

    -Showing all parts of the calculation is important because it demonstrates the step-by-step process, helps in understanding where any errors might occur, and ensures that all aspects of the problem are addressed for a complete solution.

Outlines
00:00
📚 Understanding Velocity in Kinetic Energy Equations

The paragraph begins with an introduction to the topic of calculating velocity using kinetic energy equations. The speaker presents a worksheet with questions on calculating velocity and selects question number eight as an example. The bird with a mass of 0.25 kilograms and kinetic energy of 40.5 joules is used to demonstrate the process. The key formula used is KE = (1/2)mv^2, and by rearranging and solving for v, the speaker calculates the velocity squared (v^2) and then takes the square root to find the velocity in meters per second. The result is 18 m/s. Another example is briefly mentioned, involving a hot air balloon with a mass of 1890 kilograms and a large kinetic energy value, leading to a velocity of 9 m/s. The speaker emphasizes the importance of including units and being precise in calculations to avoid losing marks.

05:01
🎓 Ensuring Completeness in Problem Solving

In this paragraph, the speaker stresses the importance of completeness in problem-solving, especially in an academic context. It is highlighted that partial solutions, such as getting only the velocity value without showing the steps, can lead to a significant loss of marks. The speaker uses a hypothetical scenario where a student gets only 2 out of 4 marks for calculating a velocity of 9 meters per second, emphasizing that a 50% score is considered a failure. The speaker concludes by encouraging viewers to aim for full marks and to not leave out any part of the problem-solving process, ensuring that they provide the equation, number substitutions, final answer, and correct units.

Mindmap
Keywords
💡Velocity
Velocity is a physical quantity that describes the rate of change of an object's position with respect to time, typically measured in meters per second (m/s). In the context of the video, velocity is the key output calculated from the given kinetic energy and mass of objects, such as a bird and a hot air balloon. The script provides examples of calculating velocity using the formula V = sqrt(KE / (0.5 * M)), where V is velocity, KE is kinetic energy, and M is mass.
💡Kinetic Energy
Kinetic energy is the energy that an object possesses due to its motion. It is defined as the work needed to accelerate the object from rest to its current velocity. In the video, kinetic energy is given in joules (J) and is used in conjunction with the mass of the objects to calculate their velocity. The formula used is KE = 0.5 * M * V^2, which can be rearranged to solve for velocity, as demonstrated with the bird and hot air balloon examples.
💡Mass
Mass is a measure of the amount of matter in an object, typically measured in kilograms (kg). In the video, mass is one of the two key inputs, along with kinetic energy, required to calculate an object's velocity. The script illustrates how mass interacts with kinetic energy in the formula for velocity, emphasizing the importance of accurate mass values in determining the speed of objects.
💡Equations
Equations are mathematical statements that assert the equality of two expressions. In the video, equations are used to relate velocity, kinetic energy, and mass, with specific focus on the rearrangement of the kinetic energy equation to solve for unknown velocities. The script demonstrates how to apply these equations to real-world scenarios involving a bird and a hot air balloon.
💡Calculation
Calculation refers to the process of performing mathematical operations to find a solution or answer. In the video, calculations are central to the demonstration of how to find the velocity of objects when given their kinetic energy and mass. The script walks through the step-by-step process of substituting values into the kinetic energy equation and performing the necessary arithmetic to arrive at the final velocity values.
💡Square Root
A square root is a mathematical operation that finds the value which, when multiplied by itself, gives the original number (the square). In the context of the video, the square root is used to extract the velocity (V) from the squared velocity (V^2) obtained by rearranging the kinetic energy equation. The script shows how to apply the square root operation to the calculated values of V^2 to find the actual velocity of the objects.
💡Physics
Physics is the natural science that studies matter, its motion, and the forces that act upon it. The video's content is rooted in physics, specifically the area of dynamics which deals with the motion of objects and the forces that cause these motions. By explaining how to calculate velocity from kinetic energy and mass, the video provides insights into the fundamental principles of physics that govern the motion of everyday objects.
💡Meters per Second (m/s)
Meters per second (m/s) is the SI unit of velocity, indicating the distance traveled in meters for each second of time. In the video, the final calculated velocities for the bird and the hot air balloon are expressed in m/s, which is a standard unit of velocity in the field of physics. The script emphasizes the importance of including the correct unit in the final answer to ensure the accuracy and context of the calculation.
💡Worksheet
A worksheet is a document or set of materials that typically includes problems or exercises to be completed, often used for educational purposes. In the video, the presenter references a worksheet with specific questions related to calculating velocity from kinetic energy and mass. The worksheet serves as a practical tool for applying the concepts discussed in the video and for practicing the related mathematical skills.
💡Comment Section
The comment section refers to the area on a video platform or webpage where viewers can post public messages or questions related to the content. In the video, the presenter encourages viewers to use the comment section to ask questions if they have any doubts or need clarification on the topic of calculating velocity from kinetic energy and mass, highlighting the interactive nature of online learning platforms.
💡Marks
In the context of the video, 'marks' refers to the points or grades that might be awarded in an educational setting for correctly solving problems. The script mentions the importance of including all necessary steps, units, and correct values in the calculations to ensure full credit is achieved. This reflects the educational aspect of the video, aiming to help viewers understand not just how to find the answer, but also how to present it in an exam or assignment setting.
Highlights

The video is an educational resource for understanding how to calculate velocity using kinetic energy equations.

The presenter uses a worksheet to guide the viewer through the process of calculating velocity.

The first example involves a bird with a mass of 0.25 kilograms and a kinetic energy of 40.5 joules.

The formula for kinetic energy (KE) is expressed as KE = 0.5 * m * V^2, where m is mass and V is velocity.

To find V^2, the equation is rearranged to V^2 = KE / (0.5 * m).

For the bird example, the calculation starts with dividing the kinetic energy (40.5 J) by half the mass (0.25 kg / 2).

The result of the division (40.5 / 0.125) gives a value of 324, which represents V^2.

To find the velocity (V), the square root of V^2 (324) must be taken, yielding a velocity of 18 m/s.

The second example features a hot air balloon with a mass of 1890 kilograms and a kinetic energy of 765,507,650 joules.

The rearranged formula for the balloon is V^2 = KE / (0.5 * m), using the balloon's mass and kinetic energy.

Dividing the kinetic energy by half the mass of the balloon (1890 kg / 2) gives a value for V^2.

The calculation results in V^2 being 81, indicating the square of the balloon's velocity.

The square root of 81 is 9, providing the velocity of the balloon as 9 m/s.

The importance of including units (m/s) in the final answer is emphasized to ensure full credit in assessments.

The video encourages viewers to participate by asking questions in the comment section.

The presenter concludes by reinforcing the need to get full marks in calculations by not omitting any steps.

Transcripts

Browse More Related Video

Solving Kinetic Energy Sample Problem with Mrs. Aki

Kinetic Energy - Introductory Example Problems

Kinetic Energy: Example Problems

How to Calculate Kinetic Energy

GCSE Physics - Kinetic Energy #2

Rotational Kinetic Energy and Moment of Inertia Examples & Physics Problems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EducationVelocity CalculationKinetic EnergyMathematics TutorialScience TeachingVideo LessonPhysics ProblemsEducational ContentLearn PhysicsMath and Science