Introduction to Centripetal Acceleration - Period, Frequency, & Linear Speed - Physics Problems
TLDRThis video delves into the concept of centripetal acceleration, explaining how it relates to an object moving in a circular path at a constant speed. It clarifies that even though the speed remains constant, the changing direction of velocity means there is an acceleration towards the center of the circle. The video further explores how this acceleration is influenced by the object's speed and the radius of the circle, providing formulas and examples to illustrate the relationship. It also covers how to calculate the speed of an object in circular motion and its period and frequency, offering practical problem-solving techniques.
Takeaways
- 🌀 Centripetal acceleration is the acceleration experienced by an object moving in a circular path at a constant speed.
- 📈 The formula for centripetal acceleration is given by a_c = v^2/r, where v is the linear speed and r is the radius of the circular path.
- 🔄 Even though the speed is constant in uniform circular motion, there is still acceleration due to the continuous change in direction.
- 📊 The direction of the centripetal acceleration vector is always towards the center of the circle, perpendicular to the velocity vector.
- 🔢 If the speed of an object in a circular path doubles, the centripetal acceleration increases by a factor of four (since (2^2) = 4).
- 📏 The relationship between the radius of the circle and centripetal acceleration is inversely proportional; as the radius increases, the acceleration decreases.
- 🚀 The period (T) of circular motion is the time taken to complete one full cycle, and frequency (f) is the number of cycles per second.
- 🔄 The circumference of a circle is given by C = 2πr, which is useful for calculating distances traveled in circular motion problems.
- 🌍 The Earth's orbit around the Sun can be approximated as a circle, and its centripetal acceleration can be calculated using the same principles.
- ✈️ For an object undergoing circular motion, like a jet turning, the centripetal acceleration can be calculated using the known linear speed and radius of the turn.
- 🌌 The gravitational acceleration on Earth (g) is approximately 9.8 m/s^2, and other accelerations can be compared to this value to understand their relative magnitudes.
Q & A
What is centripetal acceleration?
-Centripetal acceleration is the acceleration that points towards the center of a circle experienced by an object moving in a circular path at a constant speed. It is a result of the change in direction of the velocity, even though the speed remains constant.
How does the direction of velocity and acceleration vectors relate when an object is speeding up in a straight line?
-When an object is speeding up in a straight line, the direction of the acceleration vector is the same as the direction of the velocity vector, meaning they are parallel to each other.
What is the relationship between centripetal acceleration and the speed of an object moving in a circle?
-The centripetal acceleration of an object moving in a circle is directly proportional to the square of the object's speed. If the speed doubles, the centripetal acceleration increases by a factor of four (2 squared is 4).
How does the radius of a circle affect the centripetal acceleration?
-The centripetal acceleration is inversely proportional to the radius of the circle. If the radius doubles, the centripetal acceleration decreases to half its original value.
What is the formula for calculating centripetal acceleration?
-The formula for calculating centripetal acceleration is ac = V^2 / R, where V is the speed of the object and R is the radius of the circular path.
What is uniform circular motion?
-Uniform circular motion is when an object moves in a circle at a constant speed. In this case, the magnitude of the speed remains constant, but its direction is continuously changing.
How can you find the speed of an object in uniform circular motion?
-To find the speed of an object in uniform circular motion, you can use the equation V = 2πR / T, where R is the radius of the circle and T is the period, which is the time it takes for the object to complete one full cycle.
What is the period and frequency of an object in circular motion?
-The period is the time it takes for an object to complete one full cycle of circular motion, while the frequency is the number of cycles completed in one second. They are related by the equation: frequency = 1 / period.
How can you calculate the centripetal acceleration with the radius and period of circular motion?
-You can calculate the centripetal acceleration using the formula ac = 4π^2R / T^2, where R is the radius of the circle and T is the period of the motion.
What is the centripetal acceleration of the Earth around the Sun?
-The centripetal acceleration of the Earth around the Sun is approximately 5.95 × 10^-3 m/s^2. This value is calculated using the Earth's orbital radius and its period around the Sun, which is one year.
How does the centripetal acceleration experienced by a jet making a circular turn compare to Earth's gravitational acceleration?
-The centripetal acceleration experienced by a jet making a circular turn at 400 m/s with a radius of 4 km is 40 m/s^2, which is about 4.08 times the gravitational acceleration (G) at Earth's surface (9.8 m/s^2). This means the jet experiences a force slightly more than four times its normal weight during the turn.
Outlines
🚀 Understanding Centripetal Acceleration
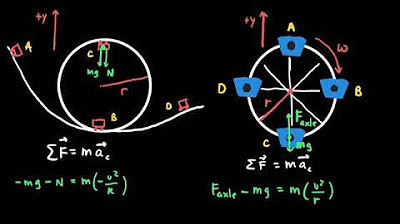
This paragraph introduces the concept of centripetal acceleration, explaining how it relates to an object's velocity. It discusses the direction of acceleration vectors in relation to velocity for objects speeding up, slowing down, moving at constant speed in a straight line, and moving at constant speed in a circular path. The paragraph emphasizes that centripetal acceleration is always directed towards the center of the circle and depends on the object's speed and the radius of the circle. It also explores the mathematical relationship between speed, radius, and centripetal acceleration, and how changes in these factors affect the overall acceleration experienced by an object in circular motion.
📏 Calculating Speed and Centripetal Acceleration
The second paragraph delves into the equations needed to calculate an object's speed and centripetal acceleration in circular motion. It introduces the relationship between distance (circumference), speed, and time, and explains how to determine the period and frequency of an object's motion. The paragraph provides a step-by-step approach to solving word problems involving centripetal acceleration, including converting units and applying the formula for centripetal acceleration. It also discusses the difference between uniform and non-uniform circular motion and how to calculate the linear speed and period of an object moving in a circle.
🌍 Earth's Orbit and Centripetal Acceleration
This paragraph applies the concepts of centripetal acceleration to the Earth's orbit around the Sun. It explains how to calculate the Earth's orbital radius and period, and then uses these values to determine the Earth's centripetal acceleration. The paragraph walks through the process of converting kilometers to meters and years to seconds, and then plugs these values into the centripetal acceleration formula. The result is a very small acceleration value, reflecting the vast scale of the Earth's orbit and its relatively slow speed compared to the gravitational pull of the Sun.
✈️ Jet Turn and Centripetal Acceleration
The fourth paragraph discusses a practical example of centripetal acceleration experienced by a jet making a circular turn. It explains how to calculate the jet's centripetal acceleration given its speed and the radius of the turn. The paragraph also compares the jet's centripetal acceleration to Earth's gravitational acceleration (G-forces), highlighting the significant force experienced during such a turn. The explanation includes unit conversions and the application of the centripetal acceleration formula, emphasizing the physical sensations that could result from high G-forces.
🌟 Gravitational Force and Acceleration
The final paragraph briefly touches on the concept of gravitational force and acceleration, specifically in the context of high G-forces experienced in rapid acceleration situations. It provides a comparison to the gravitational acceleration on Earth, explaining the physical implications of experiencing multiples of G-forces. The paragraph concludes with a hypothetical scenario of what it might feel like to experience 10 G's, reinforcing the idea that significant centripetal acceleration can have profound effects on the body.
Mindmap
Keywords
💡Centripetal Acceleration
💡Velocity
💡Uniform Circular Motion
💡Non-Uniform Circular Motion
💡Radius of the Circle
💡Frequency
💡Period (T)
💡Circumference
💡Gravitational Acceleration (g)
💡Linear Speed
Highlights
Centripetal acceleration is the acceleration experienced by an object moving in a circular path at a constant speed.
Even though the speed is constant in uniform circular motion, there is still acceleration due to the continuous change in direction.
Centripetal acceleration is always directed towards the center of the circle.
The formula for centripetal acceleration is given by $a_c = \frac{v^2}{r}$, where $v$ is the speed and $r$ is the radius of the circle.
Doubling the speed of an object in a circle results in a fourfold increase in centripetal acceleration.
If the radius of the circle is doubled, the centripetal acceleration is halved.
Reducing the radius of the circle by half results in a doubling of the centripetal acceleration.
Centripetal acceleration can be increased by a factor of 36 by reducing the radius to one-fourth and tripling the speed.
Uniform circular motion is characterized by a constant speed, but the velocity changes due to the change in direction.
The period of circular motion is the time taken to complete one full cycle.
Frequency is the number of cycles completed in one second, and it is the inverse of the period.
The linear speed of an object in uniform circular motion can be found using the formula $v = 2\pi r/T$.
An alternative formula for centripetal acceleration is $a_c = \frac{4\pi^2 r}{T^2}$, which can be used when the radius and period are known.
The Earth's orbital radius around the Sun is approximately 150 million kilometers.
The Earth takes one year to complete an orbit around the Sun.
The centripetal acceleration of the Earth in its orbit around the Sun is approximately $5.95 \times 10^{-3}$ meters per second squared.
A jet turning at a speed of 400 meters per second with a radius of 4 kilometers experiences a centripetal acceleration of 40 meters per second squared.
The centripetal acceleration experienced by the jet during the turn is equivalent to approximately 4.08 Earth gravities.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: