Lecture 6: Time Evolution and the Schrödinger Equation
TLDRThe lecture delves into the foundational concepts of Quantum Mechanics, focusing on the Schrodinger equation and its implications for time evolution and energy states. It clarifies misconceptions about wave function collapse and measurement, emphasizing the equation's linearity and unitarity. The professor illustrates how energy Eigenfunctions lead to stationary states, where probability densities remain constant over time. The discussion also touches on the superposition principle, the expansion of arbitrary wave functions in terms of energy Eigenfunctions, and the discrete energy spectra of simple quantum systems like a particle in a box.
Takeaways
- 📚 The lecture discusses the MIT OpenCourseWare initiative, which offers free access to high-quality educational resources from MIT courses.
- 🗓️ The professor clarifies that the first exam dates will be posted on the Stellar page, emphasizing the importance of checking it for updates.
- 🌌 The conversation delves into the concept of associating operators with observables in quantum mechanics, and the common misconception that operating on a wave function with an operator equates to measurement.
- 🚫 The professor strongly emphasizes that operating on a wave function with an operator is fundamentally different from measuring the observable, dispelling a frequent misunderstanding among students.
- 📈 The lecture touches on the topic of wave function collapse, explaining that it is not instantaneous and does not cease to be a function of time, which is a common point of confusion.
- 📊 The professor introduces the concept of superposition in quantum mechanics, stating that any linear combination of viable wave functions can also be a valid physical state.
- 🌟 The lecture highlights the special properties of eigenfunctions of operators corresponding to physical observables, which form a basis for any function to be expanded upon.
- 🔢 The professor explains the probabilistic interpretation of the wave function, where the probability of measuring an observable to have a particular eigenvalue is given by the norm squared of the corresponding expansion coefficient.
- 🕊️ The 'Quantum Zeno problem' is introduced, illustrating the idea that continuous measurement can effectively 'freeze' the evolution of a quantum state.
- ⏲️ The lecture discusses the properties of the Schrödinger equation, including its linearity, unitarity, and determinism, and how it governs the time evolution of quantum systems.
- 🔍 The professor addresses the question of time evolution in quantum mechanics, highlighting the apparent contradiction between deterministic evolution via the Schrödinger equation and the probabilistic nature of wave function collapse post measurement.
Q & A
What is the significance of the Creative Commons license mentioned in the script?
-The Creative Commons license allows the content, such as MIT OpenCourseWare, to be freely shared and used, supporting the dissemination of high-quality educational resources.
Why did the professor emphasize that acting on a wave function with an operator is not the same as measuring the observable?
-The professor emphasized this to clarify a common misconception. While operators are associated with observables, applying an operator to a wave function does not constitute a measurement and does not cause the wave function to collapse.
Can the concept of eigenfunctions and eigenvalues from linear algebra be related to the quantum mechanical operators and their eigenfunctions?
-Yes, in quantum mechanics, operators correspond to observables, and their eigenfunctions represent the states for which the observable has a definite value, similar to eigenvectors and eigenvalues in linear algebra.
What is the superposition principle in quantum mechanics as described in the script?
-The superposition principle states that any arbitrary linear combination of viable wave functions, which describe possible states of a quantum system, can also be a valid physical state.
What does the script imply about the relationship between the Fourier theorem and the superposition principle for momentum?
-The script implies that the Fourier theorem is a specific application of the superposition principle for the momentum operator, allowing any function to be expanded as a sum of plane waves, which are the eigenfunctions of momentum.
Why is the process of measurement described as 'disturbing' in the context of quantum mechanics?
-The process of measurement is described as disturbing because it changes the state of the quantum system from a superposition of states to a specific eigenstate corresponding to the measured observable.
What is the role of the Schrodinger equation in determining the time evolution of a quantum system?
-The Schrodinger equation is a fundamental equation in quantum mechanics that describes how the wave function of a system evolves over time. It is a deterministic equation that, given an initial wave function, allows for the calculation of the wave function at any future time.
How does the script address the issue of time evolution in quantum mechanics in relation to classical mechanics?
-The script highlights that time evolution in quantum mechanics is governed by a linear equation, unlike most classical mechanical systems where the equations are typically nonlinear. This difference leads to significant simplifications in quantum mechanics.
What is the concept of 'decoherence' mentioned in the script, and how does it relate to the measurement problem in quantum mechanics?
-Decoherence is a concept that addresses the transition of a quantum system from a superposition of states to a classical state due to interaction with the environment. It helps explain why quantum systems appear to collapse to a single state upon measurement.
What are the implications of the time-energy uncertainty relation mentioned in the script?
-The time-energy uncertainty relation implies that the more precisely the energy of a system is known, the less precisely the time it was measured can be known, and vice versa. This has implications for the accuracy of energy measurements and the concept of energy eigenstates.
Outlines
📚 Introduction to Quantum Mechanics and MIT OpenCourseWare
The script begins with an introduction to the video content provided under a Creative Commons license, highlighting the support for MIT OpenCourseWare, which offers high-quality educational resources for free. The professor then prompts for questions from previous lectures, addressing inquiries about the first exam and the association of operators with observables in quantum mechanics. The professor emphasizes the distinction between operating on a wave function with an operator and the act of measurement, clarifying that the former does not imply measurement and is a common misconception that will be further elaborated in subsequent lectures.
🔬 Quantum Mechanics Fundamentals and Eigenfunctions
This paragraph delves into the foundational aspects of quantum mechanics, focusing on the role of wave functions in defining the configuration of a system and the association of observables with operators. The professor introduces the concept of eigenfunctions, which are special functions that, when acted upon by their corresponding operator, return the same function multiplied by a constant. The eigenfunctions of the momentum operator are discussed as an example, illustrating how any function can be expanded as a superposition of these eigenfunctions, a principle that will be further explored in the context of Fourier expansions.
🌐 Superposition Principle and Wave Function Interpretation
The superposition principle is discussed in detail, explaining that any two valid wave functions can be combined to form another valid physical configuration. The audience is reminded that the eigenfunctions of operators corresponding to physical observables form a basis, allowing any function to be expressed as a linear combination of these basis functions. The paragraph also touches on the interpretation of the wave function, specifically the meaning of expansion coefficients within the context of probability and measurement outcomes.
🕰 Time Evolution in Quantum Mechanics and the Schrodinger Equation
The lecture shifts focus to the time evolution of quantum systems, introducing the concept of the collapse of the wave function upon measurement and the deterministic nature of the time evolution governed by the Schrodinger equation. The professor emphasizes the linearity of quantum evolution, contrasting it with the nonlinearity typically found in classical mechanics. The discussion also touches on the implications of continuous observation on the evolution of a quantum system, hinting at the Quantum Zeno problem.
🔄 Properties of the Schrodinger Equation and Time Reversal
This section explores the properties of the Schrodinger equation, including its linearity and unitarity, which ensures the conservation of probability. The professor addresses the audience's question about the time reversal of the Schrodinger equation, explaining that while the equation allows for both forward and backward integration in time, the act of measurement introduces a non-deterministic collapse of the wave function, leading to an apparent contradiction in the definitions of time evolution in quantum mechanics.
🚫 The Non-Local Nature of Quantum Mechanics and the Superposition Principle
The professor discusses the non-local nature of quantum mechanics, addressing the audience's question about the locality of the time evolution of the wave function. It is clarified that the energy operator in the Schrodinger equation does not inherently possess locality, which has implications for the understanding of quantum mechanics in relation to special relativity. The conversation also revisits the superposition principle, highlighting the importance of distinguishing between the linearity of the Schrodinger equation and the superposition of states postulated in quantum mechanics.
📉 Potential Pitfalls of Infinite Superpositions and Physical Relevance
The script addresses the mathematical possibility of creating discontinuous wave functions through the superposition of an infinite number of continuous functions, acknowledging the sneaky nature of such mathematical constructions. However, it is emphasized that in a physical context, such discontinuities are extremely rare and typically irrelevant, as physical systems tend not to exhibit the divergent behavior that could lead to such mathematical anomalies.
🤔 Philosophical Implications of Quantum Mechanics and the Copenhagen Interpretation
This section delves into the philosophical implications of quantum mechanics, particularly the tension between the probabilistic nature of measurement outcomes and the deterministic evolution of the wave function described by the Schrodinger equation. The professor critiques the Copenhagen interpretation, which encourages physicists to focus on computational predictions without delving into the deeper meanings or interpretations of quantum phenomena, labeling it as a 'cop out' and highlighting the dissatisfaction among some physicists with this approach.
🔬 The Theory of Decoherence and the Quantum-Classical Boundary
The professor introduces the theory of decoherence as a more satisfying narrative to reconcile the probabilistic and deterministic aspects of quantum mechanics. Decoherence suggests that the act of measurement involves the interaction of a quantum system with a macroscopic apparatus, effectively 'washing out' quantum effects and leading to the observed collapse of the wave function. This theory will be explored in more detail in later lectures, offering a potential resolution to the paradox of quantum measurement.
🎯 The Measurement Problem and the Reality of Quantum States
The script concludes with a discussion on the nature of measurement in quantum mechanics, emphasizing that while a system may be described by a superposition of states, upon measurement, it is found in a definite state. The audience is reassured that there is no ambiguity in the outcome of a measurement, and the concept of a system being in a superposition does not lead to a state of confusion or uncertainty about the result obtained.
📘 Solving the Schrodinger Equation and the Role of Energy Operators
The focus shifts to the practical aspect of solving the Schrodinger equation, highlighting the importance of specifying the energy operator for a given system. The professor outlines different strategies for solving the equation, including brute force, extreme cleverness, and numerical methods. The emphasis is on understanding the physics of the system and the value of numerical solutions in learning about the problem and validating against experimental data.
🌟 Stationary States and the Time Evolution of Energy Eigenfunctions
The script explores the concept of stationary states in quantum mechanics, which are states that remain in an energy eigenstate with a constant phase change over time. The professor explains that the probability density of finding a particle in a stationary state does not change over time, and neither do the expectation values of position or energy. This leads to the understanding that stationary states are characterized by their invariance in the face of time evolution.
🚀 General Solutions to the Schrodinger Equation via Superposition
Building on the concept of stationary states, the professor demonstrates how to construct a general solution to the Schrodinger equation using the linearity of the equation. By taking a superposition of energy eigenstates, each evolving independently over time, the professor shows that the general solution can be expressed as a sum of these eigenstates, each multiplied by a phase factor that depends on the energy of the state. This approach reduces the problem of solving the Schrodinger equation to determining the expansion coefficients for the initial condition of the system.
🔍 The Physical Relevance of Energy Eigenstates and Measurement Accuracy
The script addresses the physical relevance of energy eigenstates, acknowledging that while no real-world system is exactly in an energy eigenstate due to the continuous interaction with the environment, the concept is still valuable. The discussion turns to the accuracy of energy measurements, introducing the time-energy uncertainty relation, which implies that to measure energy with infinite precision, one would have to wait an infinite amount of time, a practical impossibility.
🌌 The Fourier Theorem and the Superposition Principle for Momentum
The professor draws a connection between the general solution to the Schrodinger equation and the Fourier theorem, highlighting the principle of superposition for the momentum operator. The eigenfunctions of the momentum operator are identified as plane waves, and the Fourier theorem is described as an application of the superposition principle for momentum, allowing any function to be represented as an integral involving these eigenfunctions and their corresponding expansion coefficients.
📍 Eigenfunctions of Position and the Expansion of Arbitrary Functions
The script concludes with a discussion on the eigenfunctions of the position operator, which are Dirac delta functions. The professor explains that while these functions are not smooth or normalizable, they can be represented as limits of sequences of reasonable functions. This allows for the expansion of arbitrary functions as superpositions of these eigenfunctions, with the expansion coefficients being the function itself evaluated at the given position.
Mindmap
Keywords
💡Creative Commons license
💡Quantum Mechanics
💡Wave function
💡Observables
💡Operators
💡Eigenfunctions
💡Superposition
💡Schrodinger equation
💡Collapse of the wave function
💡Quantum Zeno problem
💡Decoherence
Highlights
MIT OpenCourseWare's commitment to offering high-quality educational resources for free, supported by donations.
The importance of distinguishing between acting on a wave function with an operator and the process of measurement in quantum mechanics.
Clarification that the collapse of a wave function upon measurement is not instantaneous and still a function of time.
The concept of Eigenfunctions and Eigenvalues in quantum mechanics and their significance in representing observables.
The superposition principle in quantum mechanics, allowing for the combination of wave functions to describe a system.
The unique property of Eigenfunctions of operators corresponding to physical observables forming a basis for any function.
The interpretation of expansion coefficients in the context of quantum mechanics as related to the probability of measuring an observable.
The process of extracting expansion coefficients through integration, involving the wave function and its Eigenfunctions.
The deterministic nature of the Schrodinger equation, allowing for the prediction of a system's future state given its current state.
The unitary property of quantum mechanics, ensuring the conservation of probability in the time evolution of a system.
The potential violation of unitarity in the context of black holes, as related to the Hawking Effect.
The exploration of the Quantum Zeno problem, which discusses the implications of continuous measurement on a quantum system's evolution.
The explanation of time evolution in quantum mechanics as being governed by a linear equation, contrasting with classical mechanics.
The theoretical and practical challenges of measuring energy in quantum systems with absolute precision due to time constraints.
The concept of stationary states in quantum mechanics, where the probability density remains constant over time.
The use of the Fourier theorem as an example of the superposition principle for the momentum operator in quantum mechanics.
The exploration of the particle in a box model, revealing the discrete and positive nature of energy levels in quantum systems.
Transcripts
Browse More Related Video

Lecture 5: Operators and the Schrödinger Equation
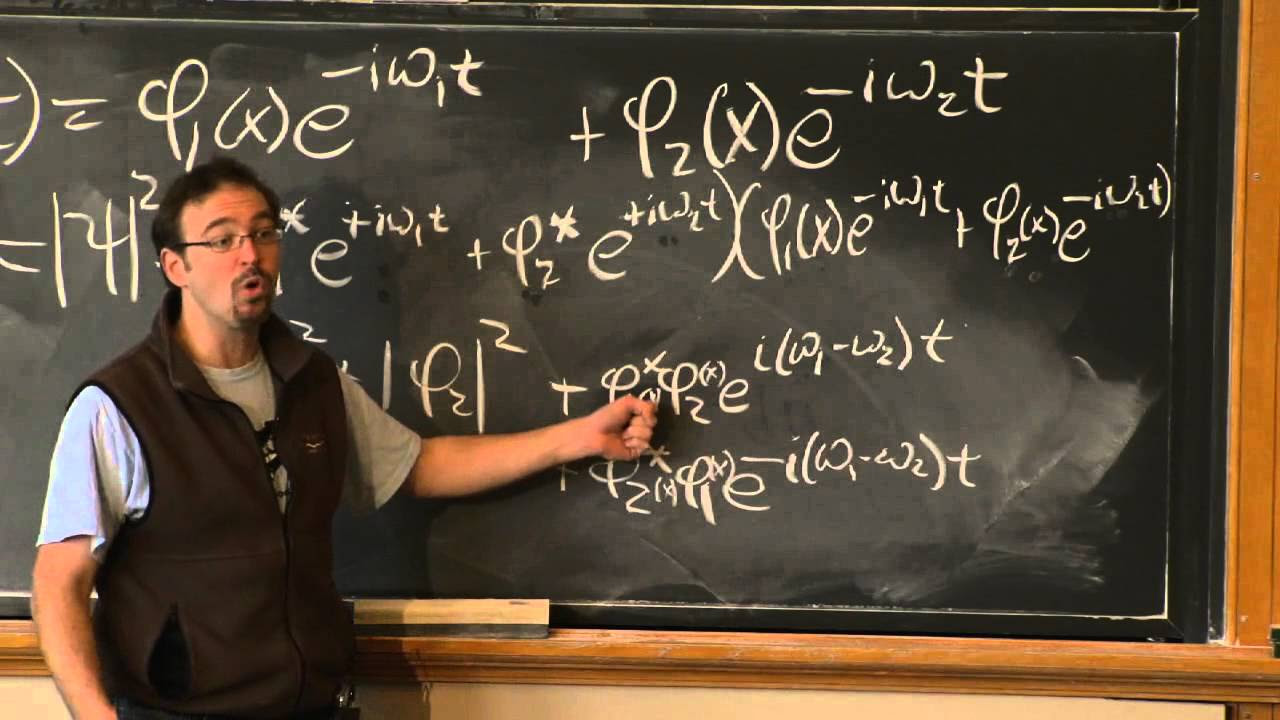
Lecture 7: More on Energy Eigenstates

22. Quantum mechanics IV: Measurement theory, states of definite energy

Quantum Physics: Part 2. Superposition. Particle in a box 🌚 Lecture for Sleep & Study

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

Lecture 4 | The Theoretical Minimum
5.0 / 5 (0 votes)
Thanks for rating: