How to Solve Doppler Effect Problems in Physics
TLDRIn this educational video, Dan the Tudor explores the Doppler effect, the phenomenon where the frequency of a sound changes as a source moves towards or away from an observer. He explains the mathematical equation behind it, using examples like an approaching car and an echo in a tunnel to illustrate how the effect works. The video clarifies the variables involved, including the observer's and source's velocities, and the medium's speed of sound, providing a practical understanding of the Doppler effect.
Takeaways
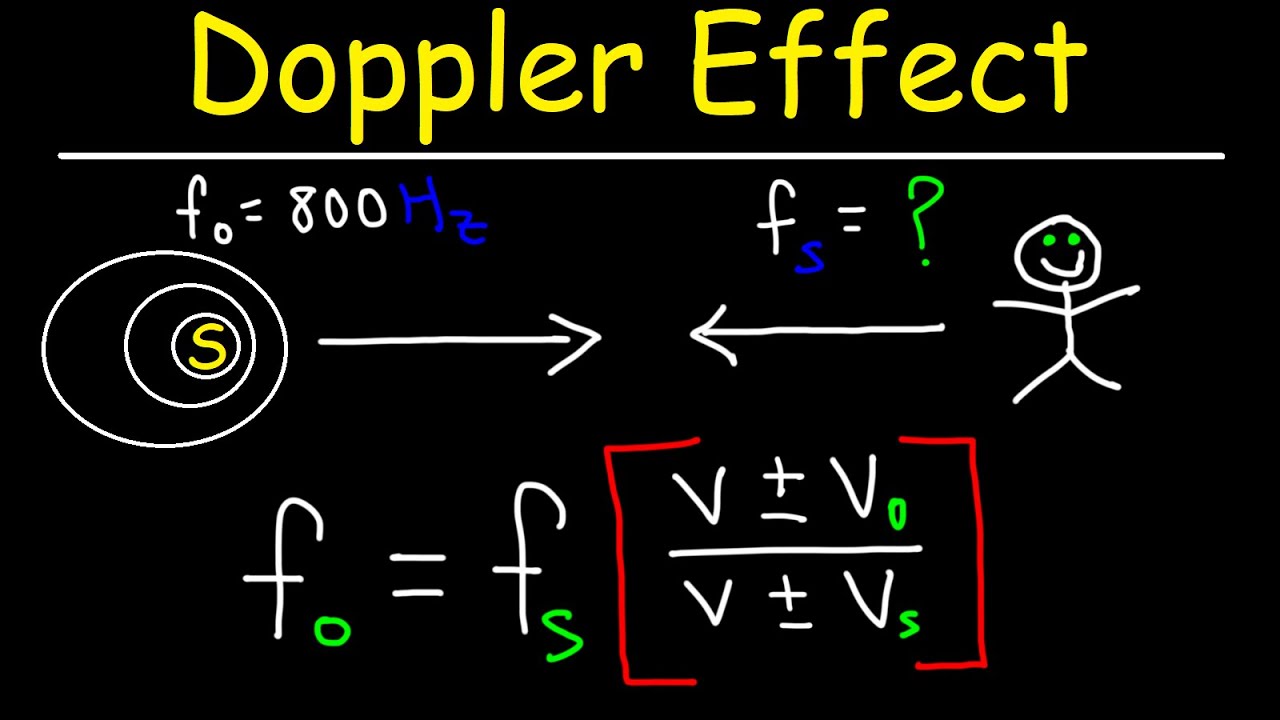
- 🚨 The Doppler effect is the change in frequency or wavelength of a wave in relation to an observer who is moving relative to the wave source.
- 🚑 The classic example of the Doppler effect is the change in pitch of a siren as an ambulance approaches and then recedes from the observer.
- 📐 The Doppler effect equation involves variables for the observer's and source's frequencies, velocities, and the speed of the medium through which the wave travels.
- 🔢 The equation uses 'o' for observer, 's' for source, 'F' for frequency, 'v' for velocity, and 'V' for the speed of the medium.
- 🎶 The speed of sound in air is commonly used as 343 meters per second in the Doppler effect calculations for sound waves.
- 🌌 The Doppler effect is not only heard in sound waves but also observed in electromagnetic waves, such as in Doppler radar and redshift in astronomy.
- 📉 When an object is moving away from the observer, the observed frequency is lower than the source frequency, and vice versa when approaching.
- 📚 The script provides an example calculation where a car's siren frequency is perceived differently by a stationary observer due to the car's movement.
- 🏃♂️ Another example involves calculating the velocity of a bear chasing a person based on the difference between the observed and actual frequency of the bear's growl.
- 🎵 The echo example demonstrates how the Doppler effect can be applied to calculate the frequency of an echo heard by a moving observer, such as a train entering a tunnel.
- 🔄 The Doppler effect equation can be used in multiple ways to solve for different variables, including the source's velocity or the observed frequency at different points.
Q & A
What is the Doppler effect?
-The Doppler effect is a change in frequency or wavelength of a wave in relation to an observer who is moving relative to the wave source. It is observed when a source of waves is moving towards or away from the observer, causing the perceived frequency to be higher or lower than the actual frequency emitted by the source.
What is the classic example of the Doppler effect?
-The classic example of the Doppler effect is the change in pitch of a siren on an ambulance or a fast car as it approaches and then moves away from an observer.
What are the variables in the Doppler effect equation?
-The variables in the Doppler effect equation are the observer's frequency (fo), source frequency (fs), observer's velocity (vo), source velocity (vs), and the speed of the medium (v), which is typically the speed of sound in air or the speed of light for electromagnetic waves.
What is the speed of sound in air, and why is it significant in the Doppler effect?
-The speed of sound in air is approximately 343 meters per second. It is significant in the Doppler effect because it is the medium's speed at which sound waves travel, affecting the observed frequency when there is relative motion between the source and the observer.
How does the Doppler effect equation account for the direction of movement?
-The Doppler effect equation uses plus and minus signs to account for the direction of movement. The top sign (+ or -) is used when the object is heading towards the observer, and the bottom sign (- or +) is used when the object is moving away from the observer.
What is the scenario in the first example provided in the script?
-In the first example, a car with a siren frequency of 1000 Hertz is moving towards a stationary observer at a velocity of 20 meters per second. The observer hears a different frequency due to the Doppler effect.
What frequency does the observer hear in the first example?
-In the first example, the observer hears a frequency of approximately 1062 Hertz, which is higher than the actual frequency of the car's siren due to the Doppler effect.
In the second example, what is the scenario and the question being asked?
-In the second example, the observer is running away from a bear at a speed of 8 meters per second and hears a frequency of 855 Hertz from the bear, whose actual frequency is 850 Hertz. The question is to determine the velocity of the bear.
What is the velocity of the bear in the second example?
-In the second example, the calculated velocity of the bear is approximately 10 meters per second, indicating that the bear is gaining on the observer despite the observer's efforts to run away.
What is the concept of an echo in the context of the Doppler effect?
-In the context of the Doppler effect, an echo is a reflected sound wave that can also exhibit the Doppler effect. The script describes a scenario where a train moving towards a tunnel emits a sound that reflects off the tunnel wall and returns to the observer at a different frequency.
What is the final observed frequency of the echo in the tunnel example?
-In the tunnel example, the final observed frequency of the echo is 4024 Hertz, which is higher than the original frequency due to the Doppler effect caused by the train's movement towards the tunnel wall.
Why was the one-kilometer distance in the tunnel example not used in the calculation?
-The one-kilometer distance in the tunnel example was not used in the calculation because the Doppler effect depends on the frequency and the speed of the source and observer, not the distance traveled by the sound wave.
Outlines
🚨 Doppler Effect Basics and Equation Explanation
This paragraph introduces the Doppler effect, a phenomenon where the frequency of a sound changes as the source moves towards or away from an observer. The classic example given is the change in pitch of an ambulance siren as it approaches and passes by. The explanation then shifts to the Doppler effect's mathematical representation, detailing the variables involved in the equation, including observer and source frequencies, velocities of both observer and source, and the speed of sound in the medium. The paragraph also clarifies the use of plus and minus signs in the equation, depending on the relative motion between the observer and the source.
🏃♂️ Calculating Bear's Velocity Using Doppler Effect
The second paragraph presents a hypothetical scenario where the observer is running away from a bear and hears a frequency of 855 Hertz, which is different from the bear's actual frequency of 850 Hertz. The task is to calculate the velocity of the bear that would result in this observed frequency difference. The explanation walks through the process of plugging the known values into the Doppler effect equation, solving for the bear's velocity, and ultimately determining that the bear is running at approximately 10 meters per second, indicating a dangerous situation for the observer.
🚂 Echoes and the Doppler Effect in a Tunnel
This paragraph delves into a more complex example involving echoes in a tunnel. The observer is on a train moving towards a tunnel wall at 50 meters per second and hears an echo with a frequency of 3000 Hertz. The challenge is to determine the frequency of the echo heard by the observer. The explanation breaks down the problem into two parts, treating the wall as a secondary observer and then as a source, and using the Doppler effect equation to calculate the observed frequency at the wall and then the final observed frequency heard by the observer on the train. The paragraph concludes with a prediction of the final answer and a discussion of alternative methods to solve the echo problem.
🎶 Multiple Methods to Solve the Echo Problem
The final paragraph provides additional methods for solving the echo problem in the tunnel scenario. It emphasizes that the distance of the cave is a red herring and that only the frequency and speed are relevant to the calculation. The explanation outlines a third method involving the observer and source both moving at the same speed and using the Doppler effect equation to find the observed frequency. The paragraph concludes by reiterating that the Doppler effect is independent of the medium's distance and ends with a sign-off and thanks to the viewers.
Mindmap
Keywords
💡Doppler Effect
💡Frequency
💡Observer
💡Source
💡Velocity
💡Speed of Sound
💡Doppler Radar
💡Redshift
💡Echo
💡Symmetric
💡Algebra
Highlights
Introduction to the Doppler effect and its audible manifestation when a vehicle approaches and passes by.
Explanation of the Doppler effect's application in Doppler radar and redshift between planets, though not the focus of the video.
Presentation of the Doppler effect equation with a detailed breakdown of its variables.
Clarification of the symbols representing Observer, source, frequency, velocity, and speed of sound in the equation.
Use of 343 meters per second as the standard speed of sound in air for most calculations.
Differentiation between the use of plus and minus in the equation based on the direction of the source and observer.
Example calculation of the perceived frequency change when a car approaches with a siren.
Demonstration of how to plug variables into the Doppler effect equation to find the observed frequency.
Scenario of running away from a bear and calculating the bear's velocity based on the Doppler effect.
Algebraic approach to solving for unknown velocities in Doppler effect scenarios.
Echo example involving a train entering a tunnel and the calculation of the frequency of the echo heard.
Method of splitting the echo problem into two parts to simplify the calculation process.
Prediction of the final answer in the echo example before performing the calculation.
Introduction of alternative methods to solve the echo example, including doubling the increase in frequency.
Final calculation confirming the predicted frequency and the explanation of the symmetry in the echo example.
Misdirection regarding the use of the tunnel's length in the problem, emphasizing the irrelevance of distance in Doppler effect calculations.
Conclusion summarizing the video's content and expressing gratitude to viewers.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: