Sound Waves
TLDRThe video script offers an insightful review of sound waves, focusing on their fundamental properties and special phenomena. It explains that sound waves are longitudinal waves, with their velocity determined by the material's bulk modulus and density. The script delves into various ways to describe sound waves, including pressure variation, density variation, and displacement of average particle location. It also illustrates how sinusoidal sound waves create areas of high and low density, with pressure changes directly related to these density fluctuations. The concept of beats is introduced, where two waves with different frequencies combine to produce a varying amplitude, resulting in a distinctive 'wah-wah' sound. Lastly, the Doppler effect is discussed, describing how the observed frequency of a sound wave changes when there is relative motion between the source and the observer. The script concludes with a clear explanation of the mathematical relationship governing the observed frequency, emphasizing the importance of understanding the direction of motion for accurate interpretation.
Takeaways
- 🌊 Sound waves are longitudinal waves, which means their particle displacement is in the direction of wave propagation, similar to a slinky.
- 📏 The speed of sound waves depends on the material's bulk modulus (B) and density (Rho), which are intrinsic properties of the medium.
- 📈 A sinusoidal sound wave can be represented by areas of high and low air molecule density, creating a wave pattern that can be plotted over time.
- 📉 The change in pressure of a sound wave is directly related to the change in density, with a sinusoidal pattern matching the density variation.
- 🔄 The amplitude of pressure changes can be different from the amplitude of density changes due to the constants involved in the material properties.
- 🌀 The average particle displacement, denoted by 's', is related to the derivative of the pressure change, resulting in a 90-degree phase shift compared to density and pressure curves.
- 🎶 Beats occur when two waves with slightly different frequencies superpose, creating an oscillating amplitude that produces a 'wah-wah' sound heard by the listener.
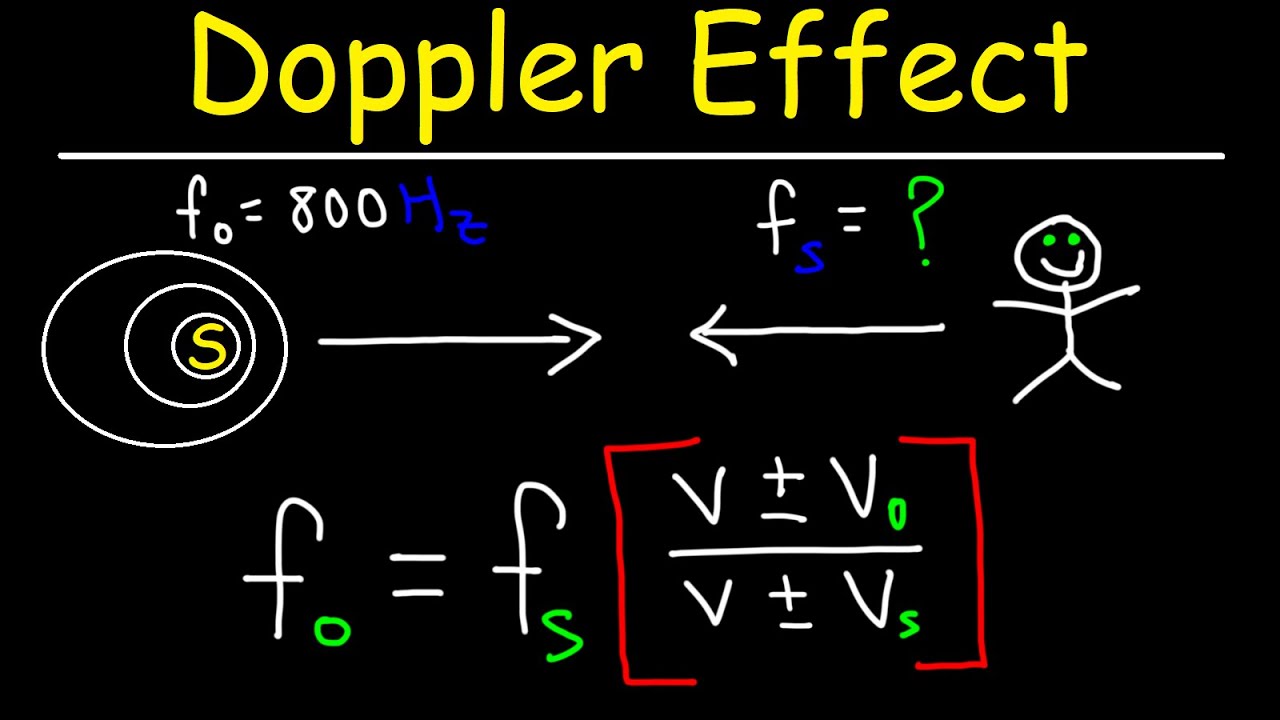
- 🚂 The Doppler effect causes a shift in the observed frequency of a sound wave when there is relative motion between the source and the observer, resulting in a higher pitch as they approach each other and a lower pitch as they move apart.
- 🔢 The frequency of beats can be calculated as the absolute difference between the two frequencies of the superposed waves.
- ↕️ The observed frequency in the Doppler effect is calculated using the emitted frequency, the speed of sound, and the speeds of the observer and source, with careful consideration of their relative directions.
- 📚 Understanding the basic properties and phenomena of sound waves is crucial for analyzing acoustic behavior in various mediums and conditions.
Q & A
What type of waves are sound waves?
-Sound waves are longitudinal waves, which means that the displacement of the medium through which they travel is in the same direction as the wave's propagation.
How does the velocity of a sound wave depend on the properties of the material it's moving through?
-The velocity of a sound wave depends on the material's bulk modulus (B) and density (Rho). The bulk modulus indicates the material's stiffness, and the density is a measure of mass per unit volume.
What is the relationship between the change in density and the change in pressure for a sound wave?
-The change in pressure is equal to the change in density times the bulk modulus divided by the baseline density (Rho naught). If the change in density is sinusoidal, then the change in pressure will also be sinusoidal.
How does the average particle displacement (denoted by 's') relate to the pressure and density changes in a sound wave?
-The change in pressure is related to the derivative of the displacement. Where there are pressure maxima or minima, the displacement will vanish, and vice versa. This means that the displacement curve is offset by 90 degrees from the density and pressure curves.
What is the phenomenon known as 'beats' and how does it occur?
-Beats occur when two waves with slightly different frequencies are superposed at the same location. The result is a wave with a varying amplitude, which produces a 'wah wah' sound. The frequency of the beats is the absolute value of the difference between the two frequencies.
How does the Doppler effect influence the perceived frequency of a sound wave?
-The Doppler effect causes a shift in the frequency of a sound wave when there is relative motion between the sound source and the observer. If they are moving towards each other, the observed frequency increases, and if they are moving away, the observed frequency decreases.
What is the formula for calculating the observed frequency (F prime) in the Doppler effect?
-The observed frequency (F prime) is calculated as the emitted frequency of the sound wave times the ratio of the speed of the observer and the source to the speed of sound, with the appropriate sign based on whether they are moving towards or away from each other.
How does the direction of motion between the observer and the sound source affect the observed frequency in the Doppler effect?
-If the observer and the sound source are moving towards each other, the observed frequency increases, resulting in a higher pitch. Conversely, if they are moving away from each other, the observed frequency decreases, leading to a lower pitch.
What is the significance of nodes and antinodes in the context of standing sound waves and harmonics?
-In standing sound waves and harmonics, nodes are points of no displacement, and antinodes are points of maximum displacement. For pressure, the nodes and antinodes are flipped compared to displacement, meaning where there is a pressure node, there is a displacement antinode, and vice versa.
What is the role of the bulk modulus in determining the properties of sound waves?
-The bulk modulus (B) is a property of the material that indicates its stiffness. It plays a crucial role in determining the velocity of sound waves and the relationship between changes in density and pressure within the sound wave.
Why is it important to consider the direction of the wave propagation when describing sound waves?
-Considering the direction of wave propagation is important because it helps to understand the nature of longitudinal waves, such as sound waves, where the displacement of particles is in the same direction as the wave's movement. This understanding is essential for analyzing phenomena like the Doppler effect and wave interference.
How does the baseline density (Rho naught) factor into the relationship between density and pressure changes in a sound wave?
-The baseline density (Rho naught) is the initial density of the medium before the sound wave is sent through it. It is used as a reference point to measure changes in density, which in turn affects the calculation of pressure changes within the sound wave.
Outlines
🌊 Understanding Sound Waves
The first paragraph introduces the topic of sound waves, focusing on their basic properties. It explains that sound waves are longitudinal, meaning their displacement is in the direction of propagation. The velocity of sound waves depends on the material's bulk modulus and density. A sinusoidal sound wave is described as being sent through a pipe, with high-density regions represented visually. The change in density is plotted, showing areas of high and low density relative to the air's density before the sound wave. The paragraph concludes with a rough sketch of the sound wave's density variation over time.
📉 Describing Sound Waves through Pressure and Displacement
The second paragraph delves into alternative ways to describe sound waves, focusing on pressure variations and displacement. It outlines the mathematical relationship between changes in air density and pressure, noting that if the density change is sinusoidal, so is the pressure change, albeit with a possible difference in amplitude due to constant factors. The displacement of air molecules, denoted by 's', is also discussed, with its relationship to the derivative of pressure. The displacement curve is shown to be offset by 90 degrees from the density and pressure curves, indicating a phase difference. This leads to a discussion on harmonics, where pressure nodes correspond to displacement antinodes and vice versa. The paragraph emphasizes the general ways to describe sound waves and sets the stage for discussing special phenomena.
🎶 Phenomena: Beats and the Doppler Effect
The third paragraph explores two special phenomena associated with sound waves: beats and the Doppler effect. Beats occur when two waves with different frequencies superpose at the same location, resulting in an oscillating amplitude that produces a 'wah-wah' sound. The frequency of the beats is the absolute difference between the two frequencies involved. The Doppler effect is described as the change in observed frequency when there is relative motion between the sound source and the observer. The observed frequency increases when the source and observer move towards each other and decreases when they move apart. The paragraph provides a formula for calculating the observed frequency and emphasizes the importance of considering the direction of motion and the correct use of plus or minus signs in the formula. The explanation concludes with a summary of the basic properties and special phenomena of sound waves.
Mindmap
Keywords
💡Sound Waves
💡Pressure Variation
💡Density Variation
💡Displacement
💡Bulk Modulus
💡Velocity of Sound
💡Beats
💡Doppler Effect
💡Harmonics
💡Sinusoidal Wave
💡Amplitude
Highlights
Sound waves are longitudinal waves that have a particular velocity depending on the material properties.
The velocity of sound waves is determined by the bulk modulus and density of the material.
Sound waves can be described in terms of pressure variation, density variation, and displacement of average particle location.
A sinusoidal sound wave in a pipe can be represented by plotting changes in density.
Pressure changes in a sound wave are sinusoidal and proportional to density changes times the bulk modulus over baseline density.
The maximum pressure changes occur at the same locations as the maximum density changes in a sound wave.
Average particle displacement in a sound wave is the derivative of pressure and is offset by 90 degrees from density and pressure curves.
Harmonics of sound waves have pressure nodes at displacement antinodes and vice versa due to the 90 degree phase shift.
Beats occur when two waves with slightly different frequencies are superposed, resulting in an oscillating amplitude and a 'wah wah' sound.
The frequency of beats is the absolute value of the difference between the two frequencies of the superposed waves.
The Doppler effect causes a shift in the observed frequency of a sound wave when there is relative motion between the source and observer.
The observed frequency increases when the source and observer are moving towards each other and decreases when moving away.
The sign of the observer and source speeds in the Doppler effect equation depends on the direction of motion relative to each other.
Remembering that observed frequency increases when moving towards each other and decreases when moving away helps solve Doppler effect problems.
This video provides a comprehensive review of the basic properties and special phenomena involving sound waves.
Transcripts
Browse More Related Video

Wave Speed on a String - Tension Force, Intensity, Power, Amplitude, Frequency - Inverse Square Law
How To Solve Doppler Effect Physics Problems

Sound: Crash Course Physics #18

Transverse and Longitudinal Waves

High School Physics - Doppler Effect

Acoustic Standing Waves and the Levitation of Small Objects
5.0 / 5 (0 votes)
Thanks for rating: