Worked example: direct comparison test | Series | AP Calculus BC | Khan Academy
TLDRThis video explores the convergence of the infinite series 1/(2^(n+1)) using the comparison test. It demonstrates that as n increases, the terms decrease rapidly due to the exponential growth of 2^n in the denominator, resembling a geometric series. By comparing it to a known convergent series, the video concludes that the series in question also converges.
Takeaways
- 🔍 The video discusses the convergence of an infinite series of the form \( \sum_{n=1}^{\infty} \frac{1}{2^n + n} \).
- 📚 The comparison test is suggested as a method to determine the convergence of the series.
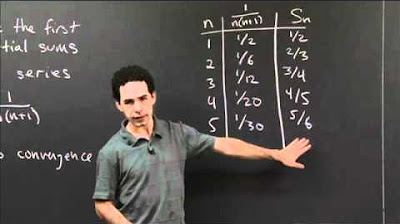
- 📝 The series is expanded for the first few terms to observe the behavior as \( n \) increases.
- 📉 The terms of the series decrease rapidly, indicating a potential convergence due to the dominance of \( 2^n \) in the denominator.
- 🔑 A key observation is made that the series behaves similarly to a geometric series \( \sum_{n=1}^{\infty} \frac{1}{2^n} \).
- 📈 The geometric series comparison is recognized as having a common ratio with an absolute value less than one, confirming its convergence.
- 📐 The comparison test criteria are reviewed, emphasizing nonnegative terms and the relationship between corresponding terms of the series.
- 📌 The series in question is compared to the geometric series, with each term of the former being less than the corresponding term of the latter.
- 📘 Since the larger series (geometric series) is known to converge, the comparison test implies that the series in question must also converge.
- 📑 The video concludes that by the comparison test, the original series converges, based on the behavior of its terms and the properties of the geometric series.
- 📝 The script encourages viewers to pause and attempt the proof themselves, promoting active learning and engagement with the material.
Q & A
What is the series being discussed in the video script?
-The series being discussed is the infinite series from n equals one to infinity of one over two to the power of n plus n.
What is the purpose of expanding the series at the beginning of the script?
-Expanding the series helps to understand its behavior as n increases and to see if the series appears to converge or diverge.
What test is suggested for determining the convergence of the series?
-The comparison test is suggested for determining the convergence of the series.
Why is the comparison test a suitable method for this series?
-The comparison test is suitable because the terms of the series get smaller as n increases, and it behaves similarly to a known convergent series, a geometric series.
What is the geometric series that the original series resembles?
-The original series resembles the geometric series from n equals one to infinity of one half to the power of n.
What condition must be met for a geometric series to converge?
-For a geometric series to converge, the absolute value of the common ratio must be less than one.
How does the script use the behavior of the terms to justify the convergence of the series?
-The script notes that as n gets larger, the term two to the power of n in the denominator grows much faster than the n in the numerator, making the terms of the series approach zero.
What is the condition for the comparison test to be applied?
-The comparison test can be applied if all terms of both series are nonnegative and the corresponding terms of the series in question are less than or equal to the corresponding terms of a known convergent series.
How does the script conclude that the series in question converges?
-The script concludes that the series converges by showing that each term of the series is less than the corresponding term of a known convergent geometric series and applying the comparison test.
What is the significance of the absolute value of the common ratio in the geometric series mentioned?
-The absolute value of the common ratio being less than one is a necessary and sufficient condition for the convergence of a geometric series.
Can you provide an example of a term from the series when n equals three?
-When n equals three, the term of the series is one over two to the third power plus three, which is one over eight plus three, or one over 11.
How does the script encourage active participation from the viewer?
-The script encourages active participation by inviting the viewer to pause the video and attempt to prove the convergence or divergence of the series on their own.
Outlines
🔍 Analyzing Convergence of an Infinite Series
The video begins with an exploration of the convergence of an infinite series, specifically the series from n=1 to infinity of one over two to the power of n plus n. The presenter suggests using the comparison test to determine if the series converges or diverges and encourages viewers to try solving it themselves. The series is expanded to show its terms, which appear to decrease rapidly, suggesting potential convergence. The behavior of the terms as n increases is analyzed, highlighting that the exponential growth in the denominator will outpace the linear growth of n, making the series behave similarly to one over two to the power of n.
📚 Recognizing a Geometric Series for Comparison
The presenter then identifies a pattern in the series that resembles a geometric series, which is the sum from n=1 to infinity of one half to the power of n. This geometric series is known to converge because the absolute value of the common ratio, one half, is less than one. The presenter uses this known convergence to set up the comparison test. The comparison test requires that the terms of the series in question are less than or equal to the corresponding terms of a known convergent series, which is the case here. The presenter demonstrates that each term of the original series is less than the corresponding term of the geometric series, fulfilling the conditions for the comparison test.
🎯 Applying the Comparison Test to Conclude Convergence
Finally, the video concludes by applying the comparison test to confirm that the original series must also converge. The presenter explains that since the geometric series with a common ratio of one half converges, and each term of the original series is less than the corresponding term of the geometric series, the original series must converge as well. The comparison test is successfully used to determine the convergence of the series, reinforcing the understanding of series behavior and convergence tests in mathematical analysis.
Mindmap
Keywords
💡Infinite Series
💡Convergence
💡Divergence
💡Comparison Test
💡Geometric Series
💡Terms
💡Denominator
💡Nonnegative
💡Corresponding Terms
💡Common Ratio
💡Absolute Value
Highlights
Introduction of an infinite series to determine if it converges or diverges.
Suggestion to use the comparison test to analyze the series.
Expansion of the series to observe its behavior for different values of n.
Observation that terms are getting smaller as n increases, indicating potential convergence.
Identification that the series behaves like 1/(2^n) for large n.
Recognition of the series as a geometric series with a common ratio of 1/2.
Explanation that the geometric series converges because the absolute value of the common ratio is less than 1.
Introduction of the comparison test criteria for series with nonnegative terms.
Application of the comparison test to the given series and the geometric series.
Demonstration that corresponding terms of the given series are less than the geometric series terms.
Conclusion that since the larger series converges, the given series must also converge based on the comparison test.
Emphasis on the importance of the terms' behavior in determining convergence.
Encouragement for viewers to pause and attempt the problem themselves.
Detailed step-by-step breakdown of the series expansion for different n values.
Graphical representation of the series terms and their decreasing nature.
Clarification of the geometric series formula and its convergence criteria.
Use of color coding to differentiate between the given series and the geometric series for comparison.
Final confirmation of the convergence of the given series using the comparison test.
Transcripts
Browse More Related Video

AP Calculus BC Lesson 10.6 Part 1

Worked example: Integral test | Series | AP Calculus BC | Khan Academy

Integral test | Series | AP Calculus BC | Khan Academy

Radius of convergence using Ratio Test
Limit of a Series | MIT 18.01SC Single Variable Calculus, Fall 2010

Worked example: limit comparison test | Series | AP Calculus BC | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: