Ch. 1.12 Modeling Variation

Prof. Williams
22 Aug 202111:20
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explores the concept of modeling and variation in natural phenomena. It explains direct and inverse proportionality, illustrating how changes in one variable affect another. The script uses examples like magnetism and gravity to demonstrate inverse proportionality, where attraction decreases as distance increases. It also covers direct proportionality and joint variation with multiple variables. The lesson includes a practical example to find the constant of proportionality and apply it to create a model. The video aims to help students grasp these mathematical relationships in real-world contexts.

Takeaways
  • πŸ“ Modeling involves relating variables to one another to understand how changes in one affect the others.
  • πŸ”„ Direct variation means two variables change in the same direction, with one being a constant multiple of the other.
  • πŸ”„ The constant multiple, k, is known as the constant of proportionality in direct variation.
  • πŸ”„ Inverse variation occurs when variables change in opposite directions, with one variable's growth resulting in the other's decrease.
  • πŸ”„ In inverse variation, the constant of proportionality is still present, but one variable becomes the reciprocal of the other.
  • 🧲 Examples of inverse proportionality include magnetism, gravity, pressure, and luminosity, where effects decrease as distance increases.
  • 🧲 The magnetic force between two magnets is inversely proportional to the square of the distance between them, following the formula F = (ΞΌ * q1 * q2) / r^2.
  • πŸ”’ To create a model, you need an input and output value to find the constant of proportionality, k.
  • πŸ”’ Solving for k in a direct variation example, such as y = 3 when x = 5, gives us k = 3/5, allowing us to predict y for different x values.
  • πŸ”„ Joint variation occurs when a variable is related to more than one other variable, involving both direct and inverse relationships.
  • πŸ”„ A model with joint variation and inverse variation might look like y = (k * a * b) / c^3, where a and b are directly proportional, and c is inversely proportional to y.
Q & A

  • What is the concept of modeling in the context of natural phenomena?

    -Modeling in the context of natural phenomena involves relating one variable to another to understand how changes in one variable affect changes in another. It's about establishing a relationship between variables to predict or explain natural processes.

  • What does it mean for variables to change directly?

    -When variables change directly, it means that as one variable increases, the other variable also increases proportionally, and vice versa. The relationship is characterized by a constant multiple, known as the constant of proportionality (k).

  • What is the constant of proportionality (k) and how does it relate to direct variation?

    -The constant of proportionality (k) is a fixed number that represents the rate at which one variable changes in relation to another in a direct variation. It is used to scale the change in one variable to determine the corresponding change in the other variable.

  • Can you provide an example of direct variation with a constant multiple?

    -An example of direct variation with a constant multiple is if x increases from 5 to 10, and y increases by half that amount, from 5 to 5.5. Here, k would be 0.5, indicating that y changes at half the rate of x.

  • What is the difference between direct and inverse variation?

    -Direct variation occurs when one variable increases as the other variable increases, while inverse variation occurs when one variable increases as the other decreases. In other words, in direct variation, variables move in the same direction, whereas in inverse variation, they move in opposite directions.

  • How is inverse variation represented mathematically?

    -Inverse variation is represented mathematically by placing the variable that decreases in the denominator of a fraction. This means as the numerator (the variable that increases) gets larger, the overall value of the fraction (the variable that decreases) gets smaller.

  • Can you explain the concept of joint variation with an example?

    -Joint variation occurs when a variable is dependent on multiple other variables, some of which it may vary directly with and others inversely with. For example, if y varies jointly with a and b but inversely with the cube of c, the model would be y = k * a * b / c^3, where k is the constant of proportionality.

  • What is the significance of the constant mu (ΞΌ) in the context of magnetic force?

    -In the context of magnetic force, mu (ΞΌ) is a constant that represents the permeability of the medium through which the magnetic force is acting. It is part of the constant of proportionality in the equation for magnetic force between two magnets.

  • How does the distance between two magnets affect the magnetic force of attraction according to the script?

    -According to the script, the magnetic force of attraction between two magnets is inversely proportional to the square of the distance between them. This means that as the distance decreases, the force of attraction increases significantly.

  • What is the equation for magnetic attractiveness between two magnets as described in the script?

    -The equation for magnetic attractiveness between two magnets is F = (ΞΌ * q1 * q2) / r^2, where F is the force of attraction, ΞΌ is the permeability constant, q1 and q2 are the charges of the magnets, and r is the distance between them.

  • How can you find the value of k in a direct variation model given two values of x and y?

    -To find the value of k in a direct variation model, you can use the formula y = kx. Given two pairs of x and y values, you can plug them into the formula and solve for k. For example, if y = 3 when x = 5, you can find k by dividing 3 by 5, resulting in k = 0.6.

Outlines
00:00
πŸ“š Introduction to Modeling and Variation

This paragraph introduces the concept of modeling natural phenomena by relating variables to each other. It explains how variables can change directly or inversely, with a focus on the constant of proportionality (k). Direct variation is illustrated with an example where y increases at half the rate of x. Inverse variation is described, contrasting it with direct variation, and using the example of magnetism to show how attraction decreases with distance. The paragraph also covers the mathematical representation of these relationships, including the formula for magnetic force between two magnets, highlighting the constants involved, such as mu and pi.

05:03
🧲 Exploring Inverse Proportionality and Magnetic Force

This paragraph delves deeper into inverse proportionality, using the example of magnetic force between magnets to illustrate how the force decreases as the square of the distance between them increases. It discusses the concept of permeability constant (mu) and how it varies in different mediums. The paragraph also explains the formula for magnetic force, breaking down the constants and variables involved, such as the charges of the magnets (q1 and q2) and the distance between them (r). It emphasizes the exponential nature of the inverse square law and provides a numerical example to demonstrate how a small distance results in a large attractive force.

10:05
πŸ” Direct Proportionality and Joint Variation

The final paragraph discusses direct proportionality with an example where y varies directly with x, and provides a step-by-step solution to find the model and the value of y when x equals a specific value. It then introduces the concept of joint variation, where a variable can vary directly with one variable and inversely with another, or even with multiple variables. The paragraph concludes with an example of joint variation, explaining how y can vary with respect to variables a and b, and inversely with the cube of variable c, and how to construct a model for such a scenario.

Mindmap
Keywords
πŸ’‘Modeling
Modeling in the context of the video refers to the process of representing natural phenomena through mathematical relationships. It is a fundamental concept in understanding how variables interact with one another. In the video, modeling is used to explain direct and inverse relationships between variables, such as how changes in one variable affect another.
πŸ’‘Variable
A variable in this video script is a symbol or number that can change within the model. It is central to the theme of the video as it discusses how variables change in relation to one another. For example, the script mentions how 'y' changes as 'x' changes, illustrating the concept of direct and inverse proportionality.
πŸ’‘Direct Proportionality
Direct proportionality is a mathematical relationship where two variables increase or decrease together. If one variable increases, the other also increases proportionally. The script uses the term to explain how two variables can be related, such as 'y' varying directly with 'x', meaning as 'x' gets larger, 'y' also gets larger by a constant multiple.
πŸ’‘Constant of Proportionality (k)
The constant of proportionality, denoted as 'k' in the script, is a factor that defines the rate at which two variables in direct proportion change in relation to each other. It is a key concept in the video's explanation of how variables change in direct proportion, as it quantifies the relationship between 'y' and 'x'.
πŸ’‘Inverse Proportionality
Inverse proportionality is a relationship where one variable increases as the other decreases, and vice versa. The video script uses this concept to explain how certain natural phenomena, like magnetism and gravity, behave. For example, the force of attraction between two magnets decreases as the distance between them increases.
πŸ’‘Magnetism
Magnetism is used in the video as an example of a phenomenon that exhibits inverse proportionality. It illustrates how the force of attraction between two magnets is inversely proportional to the square of the distance between them, demonstrating the concept with a practical application.
πŸ’‘Constant (mu)
In the context of the video, 'mu' is a constant that appears in the equation for magnetic force between two magnets. It represents the permeability of the medium, which is a key factor in determining the strength of the magnetic force. The script explains how 'mu' is used in the formula for magnetic attraction.
πŸ’‘Reciprocal
A reciprocal, as mentioned in the script, is a mathematical concept where the value of one variable is the inverse of another. This is particularly relevant in the discussion of inverse proportionality, where as one value increases, its reciprocal decreases, and vice versa.
πŸ’‘Joint Variation
Joint variation is a concept where a variable is related to multiple other variables in a combined manner, some directly and some inversely. The video script introduces this idea by explaining how 'y' can vary jointly with 'a' and 'b', and inversely with the cube of 'c', illustrating the complexity of relationships in modeling.
πŸ’‘Cube
The cube of a number, as discussed in the script, is the result of multiplying the number by itself three times. In the context of joint variation, the cube of 'c' is used to show how the variable 'y' is inversely proportional to the cube of 'c', meaning as 'c' increases, 'y' decreases more rapidly due to the cubic relationship.
Highlights

Introduction to modeling natural phenomena by relating variables and their changes.

Explanation of direct variation between variables, where changes in one variable affect the other proportionally.

Introduction of the constant of proportionality, denoted as 'k', in direct variation models.

Illustration of direct variation with an example of variable 'y' growing half as fast as 'x'.

Introduction to inverse variation, where an increase in one variable results in a decrease in the other.

Clarification of inverse variation with an example of 'y' being the reciprocal of 'x'.

Demonstration of inverse variation with the example of magnetism and gravity.

Explanation of how the magnetic force between two magnets is inversely proportional to the square of the distance between them.

Introduction of the equation for magnetic attractiveness, including the constant of proportionality 'mu'.

Discussion on how the permeability constant 'mu' can vary in different mediums.

Explanation of the variables in the magnetic force equation, including the charges of the magnets and the distance between them.

Example calculation demonstrating how a small distance between magnets results in a large attractive force.

Solving a word problem to find the model of direct proportionality between 'y' and 'x'.

Introduction to joint variation, where a variable can vary with more than one other variable.

Explanation of how to model joint variation with a combination of direct and inverse relationships.

Emphasis on the importance of having only one constant of proportionality in any given model.

Conclusion of the chapter with a summary of the key concepts covered on modeling and variation.

Transcripts

Browse More Related Video

Calculus AB/BC – 7.1 Modeling Situations with Differential Equations

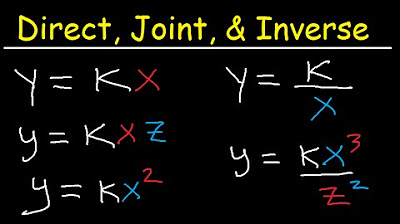
Direct Inverse and Joint Variation Word Problems

Resistance & Resistivity - How Temperature Affects Resistance

2021 Live Review 3 | AP Physics 1 | Understanding Circular Motion and Gravitation

Simple harmonic motion and angular frequency [IB Physics SL/HL]

AP Physics Workbook 2.A Relationship Between Force and Acceleration

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ModelingVariationDirect ProportionalityInverse ProportionalityConstant of ProportionalityMagnetismGravityPhysicsEducationalMath ConceptsNatural Phenomena