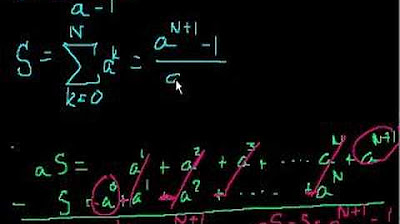Things get weird at infinity
TLDRThis video explores the fascinating concept of infinity in mathematics, demonstrating how it challenges our intuition through various paradoxical examples. It delves into the storage capacity required to hold every possible digital image, the sum of infinite series, and the surprising equivalence in size between different infinite sets. The video also teases an upcoming exploration of fractals and chaos theory, sponsored by CuriosityStream, offering a platform for curious minds to delve into a vast library of documentaries.
Takeaways
- 🌐 The video is sponsored by CuriosityStream, a platform offering over 2,500 documentaries and non-fiction titles for curious minds.
- 🖼️ It's theoretically possible to store every possible 12-megapixel digital image on a computer with a sufficiently large storage capacity, despite the number being astronomically large.
- 🎨 Each pixel in a 12-megapixel image can display one of over 16 million color options, leading to a vast number of potential images.
- 🔢 The concept of infinity in mathematics can lead to seemingly paradoxical results, such as different sums for an infinite grid of numbers based on the order of addition.
- 📊 The sum of an infinite geometric series where each term is half the previous one converges to one, which is a fundamental property used in analyzing infinite series.
- 🔄 Rearranging the terms of an infinite series can change the sum, as demonstrated by the alternating harmonic series versus a rearranged version leading to different results.
- 📉 The difference in sums for rearranged series is attributed to the series' convergence properties, with conditionally convergent series being more susceptible to changes in sum due to order.
- 🔶 The size of infinite sets can be compared using the concept of one-to-one correspondence, where each element in one set can be uniquely mapped to an element in another without overlap.
- 🔍 The set of all positive integers and the set of all positive even integers have the same size (cardinality) because they can be mapped one-to-one and onto each other.
- 🤔 The set of all real numbers between 0 and 1 (excluding both endpoints) is shown to have the same size as the set of all real numbers, which counters intuitive expectations.
- 🛑 The addition or removal of a single element from an infinite set does not change its size, as demonstrated by the mapping of all numbers between 0 and 1 with and without the endpoint 0.
Q & A
What is the main topic of the video?
-The main topic of the video is the exploration of the concept of infinity in mathematics, particularly in relation to digital images, infinite sums, and set theory.
Can every possible digital image be stored on a computer with a large amount of storage?
-Yes, theoretically, every possible digital image could be stored on a computer with a sufficiently large amount of storage, considering a finite number of pixel resolutions and color options.
What is the maximum number of color options per pixel in a standard 24-bit color representation?
-In a standard 24-bit color representation, there are more than 16 million color options per pixel.
What is the concept of absolute convergence in the context of infinite series?
-Absolute convergence refers to a series where the sum of the absolute values of its terms converges to a finite number, allowing the sum to be independent of the order of terms.
How does the video demonstrate the concept of conditional convergence in series?
-The video demonstrates conditional convergence by showing that changing the order of terms in a series can lead to different sums, which only happens when the series is not absolutely convergent.
What is the significance of the Cantor set in the video?
-The Cantor set is mentioned as an introduction to the mathematics of fractals and is highlighted for its surprising properties related to infinity.
What is the relationship between the set of all positive integers and the set of all positive even integers in terms of size?
-The set of all positive integers and the set of all positive even integers are the same size or cardinality because there is a one-to-one correspondence between the elements of both sets.
How does the video explain the concept of mapping in set theory?
-The video explains mapping in set theory by showing that two sets can have the same size or cardinality if there is a one-to-one and onto relationship between their elements, even when dealing with infinite sets.
What is the paradox presented in the video regarding the sum of an infinite grid of numbers?
-The paradox is that the sum of the entire grid can be both zero and negative two, depending on whether the sum is calculated by rows or by columns, highlighting the importance of order in infinite sums.
What is the significance of the alternating harmonic series in the video?
-The alternating harmonic series is used to illustrate how rearranging the terms of an infinite series can change its sum, even though the terms themselves remain the same.
What is the conclusion of the video regarding the size of sets with infinitely many elements?
-The conclusion is that the size or cardinality of sets with infinitely many elements can be the same even if they seem different, as demonstrated by the examples of positive integers, even integers, and real numbers between 0 and 1.
Outlines
🌌 The Finite Possibilities of Infinite Images
This paragraph explores the theoretical capacity of digital storage to contain every possible image, focusing on 12-megapixel images as a standard for human visual acuity. It explains that each pixel can display one of over 16 million colors, determined by a 24-bit number, leading to an astronomical number of potential images. The script also touches on the philosophical concept of infinity in mathematics, contrasting it with the finite, yet vast, number of digital images that could theoretically exist.
🔢 Paradoxes of Infinite Summation
The script delves into the complexities of summing infinite series, using a grid of numbers to illustrate how the order of addition can affect the outcome. It introduces the concept of geometric series and demonstrates how rearranging terms can lead to different sums, even though the series contains the same numbers. This is exemplified through the alternating harmonic series, showing how a change in the order of terms can alter the sum from the natural log of 2 to approximately 1.04, highlighting the importance of convergence in series and the impact of conditional versus absolute convergence.
🔗 Mapping the Sizes of Infinite Sets
This section discusses the counterintuitive nature of infinity in set theory, particularly the concept of cardinality. It explains how infinite sets, such as all positive integers and all positive even integers, can have the same size due to a one-to-one correspondence. The script further explores the surprising fact that the set of all real numbers between 0 and 1 (excluding 1) is the same size as the set of all real numbers, challenging intuitive notions of size. It also presents a thought experiment involving the inclusion of 0 in the set, demonstrating that even adding an infinite number of elements to a set does not change its size when dealing with infinite sets.
🎥 CuriosityStream: Sponsor and Preview of Related Content
The final paragraph shifts focus to the sponsor of the video, CuriosityStream, which offers a platform for documentaries and non-fiction content. It promotes a documentary series exploring chaos theory, fractals, and their applications in various fields, including computer systems and population modeling. The script concludes with an invitation for viewers to sign up for CuriosityStream using a provided link for a free trial, emphasizing the breadth of content available for math and science enthusiasts.
Mindmap
Keywords
💡CuriosityStream
💡Infinite Storage
💡12-Megapixel Images
💡Color Depth
💡Geometric Series
💡Infinite Sum
💡Alternating Harmonic Series
💡Conditionally Convergent
💡Cardinality
💡One-to-One Correspondence
💡Cantor Set
Highlights
Sponsored video by CuriosityStream, a platform with over 2,500 documentaries for curious minds.
The theoretical possibility of storing every conceivable digital image, given sufficient storage capacity.
Explaining the finite number of 12-megapixel images possible by calculating pixel color variations.
The paradox of infinite sums in mathematics, where different methods can yield different results.
Demonstration of a grid sum that equals zero by rows but negative two by columns, showcasing the importance of order in infinite sums.
The concept of conditional convergence in infinite series and its impact on the sum's sensitivity to term order.
The surprising result that the set of all positive integers has the same size as the set of all positive even integers.
The counterintuitive fact that the set of real numbers between 0 and 1 is the same size as all real numbers.
A challenging problem about the size of sets of real numbers including and excluding 0 and 1, with a surprising conclusion.
The mapping technique used to prove that sets with and without 0 and 1 are the same size.
Introduction to the Cantor set as an intriguing example of infinity's properties and its relation to fractals.
The connection between mathematical patterns and chaos theory, with a teaser for a future video on the topic.
Promotion of CuriosityStream's documentary 'The Secret Life of Chaos' exploring chaos, order, and patterns in nature and mathematics.
Offer of a free first month's membership to CuriosityStream for new subscribers using a provided link.
Acknowledgment of Patreon supporters and an invitation to follow the creator on social media for updates.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: