Finding Pi by Archimedes' Method
TLDRThe script details Archimedes' method for approximating the value of pi using polygons inscribed in a circle. Starting with a hexagon and doubling the number of sides, the process involves using the Pythagorean theorem to calculate the side lengths of increasingly complex polygons. By employing a spreadsheet to automate the calculations, the script demonstrates how to iteratively refine the approximation of pi, showcasing the convergence towards the well-known mathematical constant.
Takeaways
- 📏 The ratio of a circle's circumference to its diameter is known as Pi, and it is approximately between three and four.
- 🔍 Archimedes, around 200 BC, devised a method to calculate Pi with high precision using polygons inscribed within a circle.
- 🔨 Starting with a hexagon, the process involves doubling the number of sides of the polygon to approximate Pi more accurately.
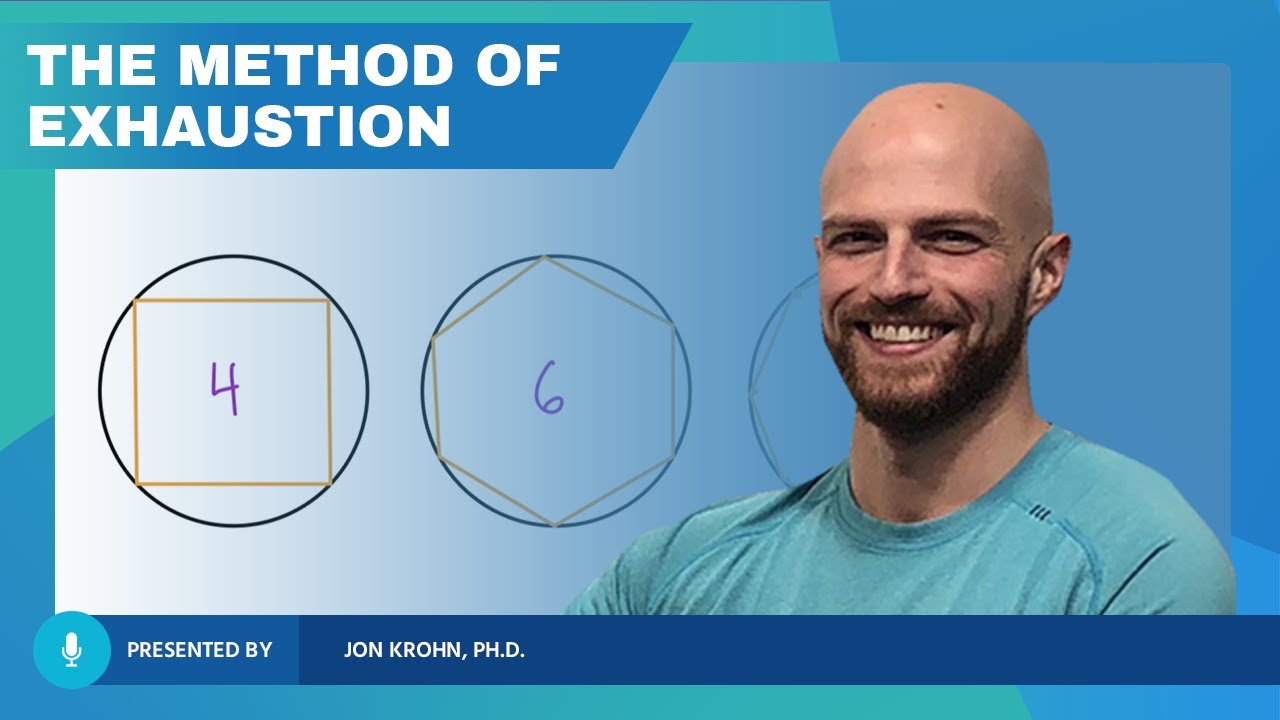
- 📐 The first approximation of Pi is obtained by considering a hexagon inscribed in a circle, yielding a ratio of 6 over 2, or 3.
- 📈 To find the side length of polygons with more sides, the Pythagorean theorem is applied to the right triangles formed by the polygon's sides and the circle's radius.
- 📉 The length of the side of a 12-sided figure is calculated by taking the square root of the difference between the square of the radius (1) and the square of half the side of the hexagon.
- 📝 The process of finding the side length for polygons with more sides involves a three-step process using the Pythagorean theorem and subtraction from the radius.
- 📋 Spreadsheets can be used to automate the calculations for polygons with an increasing number of sides, thus refining the approximation of Pi.
- 🔢 As the number of sides increases, the approximation of Pi stabilizes, with more digits remaining constant the further the calculations go.
- 🔄 Archimedes manually calculated Pi up to a 96-sided figure, while modern tools allow for even more precise calculations with less effort.
- 🔗 The value of Pi computed using the polygon method in the script matches the value typically stored in calculators and spreadsheet programs.
Q & A
What is the ratio of a circle's circumference to its diameter known as?
-The ratio of a circle's circumference to its diameter is known as Pi (π).
Who is credited with developing a method to calculate Pi with more precision?
-Archimedes, around 200 BC, is credited with developing a method to calculate Pi with more precision.
How did Archimedes initially approach the calculation of Pi?
-Archimedes initially approached the calculation of Pi by inscribing a polygon, specifically a hexagon, inside a circle.
Why is a hexagon a good starting point for approximating Pi?
-A hexagon is a good starting point because it is six times as far around as the radius, making the initial ratio of the perimeter to the diameter 3, which is a simple and close approximation of Pi.
What mathematical theorem is used to find the length of a side of a 12-sided figure given the side length of a hexagon?
-The Pythagorean theorem is used to find the length of a side of a 12-sided figure given the side length of a hexagon.
How does the method of doubling the number of sides of a polygon help in approximating Pi?
-Doubling the number of sides of a polygon increases the accuracy of the approximation of Pi because it reduces the error in the perimeter relative to the diameter of the circle.
What is the formula for calculating the new side length (S2) of a polygon with twice the number of sides?
-The formula for calculating S2 is the square root of (B squared + (S1/2) squared), where B is 1 minus A, and A is the square root of (1 - (S1/2) squared).
How can a spreadsheet be used to automate the calculation of Pi using Archimedes' method?
-A spreadsheet can be used to automate the calculation by setting up formulas that calculate the new side lengths and perimeters for polygons with increasing numbers of sides, thus iteratively approximating Pi.
What is the significance of the number 3.14 in the context of Pi?
-The number 3.14 is a commonly recognized approximation of Pi, and it is the result of the method described when using a sufficiently high number of sides in the polygon.
How does the accuracy of the Pi approximation improve as the number of sides of the polygon increases?
-The accuracy improves because with more sides, the perimeter of the polygon more closely matches the actual circumference of the circle, leading to a more precise ratio of the perimeter to the diameter.
What is the maximum number of decimal places of Pi that the spreadsheet in the script was able to calculate?
-The spreadsheet in the script was able to calculate Pi to approximately 10 decimal places (3.1415926535) before reaching the limit of its numerical capacity.
Outlines
📐 Introduction to Archimedes' Method for Calculating Pi
This paragraph introduces the historical context of pi's calculation, mentioning Archimedes' method from around 200 BC. It explains the initial approximation of pi by using the perimeter of a hexagon inscribed in a circle and the ratio of the perimeter to the diameter. The method involves doubling the number of sides of the polygon to increase the accuracy of pi's approximation, starting with a hexagon and progressively moving to 12, 24, and more sides. The paragraph also poses a question about how to find the side length of a 12-sided figure given the length of a hexagon's side, setting the stage for the mathematical explanation to follow.
🔍 Detailed Explanation of Archimedes' Polygon Doubling Technique
The paragraph delves into the specifics of how to calculate the side length of a 12-sided polygon, starting with a hexagon. It describes the process of bisecting the sides of the hexagon to create a 12-sided figure and then using the Pythagorean theorem to find the new side length. The explanation includes finding the midpoint of a side, drawing a radius to the midpoint, and using the Pythagorean theorem to calculate the new side length 'a' and the distance 'b' from the midpoint to the circle. The process is iterative, with each step building on the previous to refine the approximation of pi.
📈 Utilizing Spreadsheets to Automate Archimedes' Method
This paragraph discusses the practical application of Archimedes' method using modern spreadsheet software to automate the calculations. It outlines the steps for setting up a spreadsheet, labeling columns for the number of sides, side length, and intermediate calculations. The process involves using formulas to calculate the new side length 'a', the distance 'b', and the new side length 's2' for each iteration. The paragraph demonstrates how to pull down formulas to apply them to subsequent rows, doubling the number of sides with each iteration, and how to calculate the perimeter and use it to estimate pi.
🔢 Spreadsheet Calculation and Pi's Approximation
The final paragraph wraps up the process by illustrating the use of the spreadsheet to calculate pi to a high degree of accuracy. It shows the progression of calculations for polygons with increasing numbers of sides, leading to an approximation of pi that is accurate to several decimal places. The paragraph also compares the spreadsheet's calculated value of pi with the value typically found on scientific calculators, noting the remarkable similarity. It concludes by emphasizing the method's effectiveness in approximating pi and the potential for further precision with more advanced computational tools.
Mindmap
Keywords
💡Circumference
💡Diameter
💡Polygon
💡Hexagon
💡Pythagorean Theorem
💡Radius
💡Approximation
💡Archimedes
💡Spreadsheet
💡Precision
Highlights
The concept that the circumference of a circle is approximately three times its diameter, introducing the concept of pi.
Archimedes' method from around 200 BC for finding pi with increasing precision using polygons inside a circle.
Starting with a hexagon and using the Pythagorean theorem to find the side length of a 12-sided figure.
The process of doubling the number of sides of a polygon to approximate pi more closely.
Using the Pythagorean theorem to calculate the unknown side of a right triangle formed within the polygon.
The formula for finding the length 'a' using the radius and half the side length of the polygon.
Calculating the distance 'B' from the circle's edge to the midpoint of a side using the radius and length 'a'.
Finding the new side length 'S2' for the next polygon using the Pythagorean theorem with 'B' and half the original side.
Archimedes' manual computation of polygons up to 96 sides to approximate pi.
Advantages of modern math notation and tools for simplifying the computation of pi.
Using a spreadsheet to automate the calculation of pi using polygons with increasing sides.
The spreadsheet formula for calculating the half side length and its application in subsequent rows.
Automating the calculation of 'a' and 'B' using spreadsheet formulas that reference the same row.
The iterative process of pulling down formulas in a spreadsheet to calculate pi for polygons with more sides.
Observing the convergence of calculated pi values as the number of polygon sides increases.
The comparison of the spreadsheet's embedded value of pi with the calculated value using polygons.
The practical limit of the spreadsheet program in calculating pi due to the maximum number size it can handle.
Achieving a high precision estimate of pi using a 25,165,000-sided polygon within the spreadsheet's capabilities.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: