MOMENTUM - Everything You Need To Know! | GCSE & IGCSE Physics | AQA, Edexcel, OCR, CIE

Science with Hazel

24 Mar 202112:46

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video delves into the concept of momentum, highlighting its vector nature and conservation principle. It explains the momentum equation, mass times velocity, and its units. Through various examples, the video illustrates how to calculate momentum and force, and how safety features like crumple zones and seat belts reduce injury in car crashes by increasing the time over which momentum change occurs, thereby decreasing force. It also covers recoil velocity and the impact of throwing objects on an individual's motion, emphasizing the importance of understanding momentum in physics.

Takeaways

📚 Momentum is a vector quantity with both direction and magnitude, measured in kilograms meters per second (kg m/s).
🔄 The principle of conservation of momentum states that the total momentum before an event is equal to the total momentum after the event.
🚚 An example calculation involves a truck and another truck colliding and sticking together, where the combined mass and common velocity after the collision can be determined using conservation of momentum.
🔫 Recoil velocity problems, such as a person firing a rifle, can be solved by understanding that the initial momentum of the person is zero, and the final momentum is shared between the person and the bullet.
⚖️ The equation force equals change in momentum over time (F = Δp/Δt) is key to understanding how force impacts an object's motion.
🚗 Cars have safety features like crumple zones, seat belts, and airbags that work by increasing the time over which a change in momentum occurs, thus reducing the force experienced during a collision.
🎯 To calculate the force acting on a car during acceleration or a crash, you can use the change in momentum and the time taken for that change.
🛡️ Besides seat belts, other safety features in cars that reduce the risk of injury include airbags and crumple zones, which help to distribute the force of a collision over a larger area and time.
🤸‍♂️ In a scenario with an ice skater throwing a snowball, the conservation of momentum can explain why the skater moves in the opposite direction to the snowball after throwing it.
🛹 When a boy jumps onto a stationary skateboard, the conservation of momentum can be used to calculate the new combined velocity of the boy and the skateboard.
💥 In a crash test scenario, the average force on a car can be calculated by dividing the change in momentum by the time it took for the car to stop.

Q & A

What is momentum and how is it defined in physics?
-Momentum is a vector quantity, meaning it has both direction and magnitude (size). It is defined as the product of an object's mass and velocity.
What is the equation for momentum and its units?
-The equation for momentum is mass times velocity (p = mv). The units of momentum are kilograms meters per second (kg·m/s).
How is momentum conserved in collisions?
-Momentum is conserved in collisions, meaning the total momentum before the collision is equal to the total momentum after the collision.
How do you calculate the common velocity after a collision if two objects stick together?
-To calculate the common velocity after a collision where two objects stick together, sum their individual momenta before the collision and divide by their combined mass.
What is the recoil velocity and how is it calculated?
-Recoil velocity is the velocity at which an object moves backward after ejecting another object. It is calculated using the conservation of momentum principle: momentum before equals momentum after.
How do you determine the force acting on an object given its change in momentum and time taken?
-Force is determined by dividing the change in momentum by the time taken for that change (F = Δp/Δt).
What role do crumple zones and seat belts play in reducing injury during car crashes?
-Crumple zones and seat belts increase the time over which the change in momentum occurs, reducing the force felt by the occupants according to the equation F = Δp/Δt.
What is the significance of negative velocity in recoil problems?
-Negative velocity indicates that the object is moving in the opposite direction to the initial motion, consistent with the principle of conservation of momentum.
How do you calculate the velocity of a car given its mass and the force acting on it?
-Velocity is calculated by dividing the product of the car's mass and the change in velocity by the time over which the force acts, using the equation F = Δp/Δt.
How do you calculate the momentum of an object given its mass and velocity?
-Momentum is calculated by multiplying the object's mass by its velocity (p = mv).

Outlines

00:00

🚚 Momentum and Collision Dynamics

This paragraph introduces the concept of momentum as a vector quantity with both direction and magnitude, measured in kilograms meters per second. It explains the key equation for momentum, which is mass times velocity, and highlights the principle of conservation of momentum, stating that the total momentum before and after an event remains constant. The paragraph provides an example of a collision between two trucks, demonstrating how to calculate their common velocity after the collision using the conservation of momentum principle.

05:01

🔍 Recoil Velocity and Momentum Conservation

The second paragraph delves into the application of momentum conservation in recoil velocity problems. It uses the example of a person firing a rifle to illustrate how to calculate the velocity of the person moving backward due to the bullet's momentum. The explanation includes the setup of the equation for momentum before and after the event, emphasizing that the initial momentum of the person is zero, and the final momentum is the sum of the person's and the bullet's momentum. The calculation results in the person's recoil velocity, which is expected to be in the opposite direction of the bullet's velocity.

10:05

🛡️ Force, Momentum, and Car Safety Features

This paragraph explores the relationship between force, momentum, and time, particularly in the context of car safety. It explains how safety features like crumple zones, seat belts, and airbags work by extending the time over which a momentum change occurs, thereby reducing the force experienced by the occupants during a collision. The paragraph also touches on how to calculate the force acting on a car during acceleration and deceleration, using the equation force equals change in momentum over time. It concludes with examples of how to apply these concepts to answer questions about car safety and physics problems involving momentum.

❄️ Momentum in Ice Skating and Everyday Examples

The final paragraph presents everyday examples to further illustrate the concept of momentum, including an ice skater throwing a snowball and a boy jumping onto a stationary skateboard. It explains how the conservation of momentum can be used to calculate the initial momentum of the snowball and the combined velocity of the boy and the skateboard after he lands on it. The paragraph emphasizes the principle that the total momentum before and after an event remains the same, and it uses this principle to solve the given problems.

Mindmap

Keywords

💡Momentum

Momentum is a fundamental concept in physics, defined as the product of an object's mass and velocity. It is a vector quantity, meaning it has both magnitude and direction. In the video, momentum is central to understanding how objects interact during collisions, with the key equation being mass times velocity, resulting in units of kilograms meters per second. The script uses the momentum concept to explain phenomena such as the conservation of momentum in collisions and recoil velocity.

💡Conservation of Momentum

The conservation of momentum principle states that the total momentum of a closed system remains constant if no external forces act upon it. In the video, this principle is repeatedly applied to solve problems involving collisions, where the total momentum before the collision equals the total momentum after the collision, regardless of the objects' individual velocities post-collision.

💡Vector

A vector is a quantity that has both magnitude and direction. In the context of the video, momentum is described as a vector because it depends on both how much (mass) and the direction in which an object moves (velocity). This is crucial for understanding the dynamics of moving objects, especially in collision problems.

💡Collision

A collision is an event in which two or more bodies exert forces on each other for a very short period of time. The video script discusses collisions, particularly elastic collisions where objects stick together after impact, and uses them to illustrate the application of the conservation of momentum.

💡Recoil Velocity

Recoil velocity refers to the change in velocity of an object as a result of a force exerted by another object. The script provides an example where a person fires a rifle, and the bullet's momentum is transferred to the person, causing them to move backward with a recoil velocity, demonstrating the conservation of momentum.

💡Force

Force is the interaction that causes a change in the motion of an object. In the video, force is related to the change in momentum over time. It is used to calculate the force acting on a car during acceleration or during a crash, where the change in momentum is divided by the time over which the change occurs.

💡Crumple Zones

Crumple zones are structural components in vehicles designed to absorb and disperse the energy of a collision. The video explains that when a car with a crumple zone collides with an object, the front bumper collapses, increasing the time over which the momentum change occurs, thus reducing the force experienced by the occupants and preventing serious injury.

💡Seat Belts

Seat belts are safety devices in vehicles that secure the occupants and prevent them from being thrown around during a collision. The script describes how seat belts work by extending during a crash, which increases the time over which the change in momentum occurs, thereby reducing the force on the person and mitigating the risk of injury.

💡Airbags

Airbags are safety features in vehicles that inflate rapidly during a collision to cushion the impact. Although not explicitly detailed in the script, airbags are mentioned alongside crumple zones and seat belts as part of the safety features that help reduce the risk of serious injury in a car crash by increasing the time of impact.

💡Significant Figures

Significant figures refer to the digits in a number that carry meaning contributing to its precision. The video script mentions rounding the recoil velocity to three significant figures, which is a common practice in scientific calculations to express the precision of the result.

💡Newtons

Newtons are the unit of force in the International System of Units (SI). The script uses the term when calculating the force acting on a car during acceleration or a crash, where the change in momentum is divided by the time to yield the force in newtons.

Highlights

Momentum is a vector quantity with both direction and magnitude.

The unit of momentum is kilograms meters per second (kg m/s).

Momentum is conserved in collisions, meaning the total momentum before and after an event remains the same.

Calculating the common velocity after a collision using the conservation of momentum principle.

Recoil velocity problems can be solved using the conservation of momentum concept.

Force is equal to the change in momentum over time, which is key to understanding motion dynamics.

Crumple zones, seat belts, and airbags are safety features that reduce the force experienced in a car crash by extending the time over which momentum changes.

The equation linking momentum, mass, and velocity is momentum = mass × velocity.

An example of calculating the momentum of a wet cloth thrown at empty tins.

The importance of understanding the conservation of momentum in collisions involving multiple objects.

How seat belts reduce the risk of serious injury in car crashes by distributing the force over a longer period.

Calculating the velocity of a car with the same momentum as a truck using the conservation of momentum.

Determining the average force on a car during a crash test using the change in momentum over time.

An ice skater throwing a snowball and the conservation of momentum causing her to move in the opposite direction.

Calculating the combined velocity of a boy and a skateboard after he jumps on it, using conservation of momentum.

The video concludes with a summary of key points and practical applications of momentum in real-world scenarios.

Transcripts

Browse More Related Video

Changes In Momentum | Forces & Motion | Physics | FuseSchool

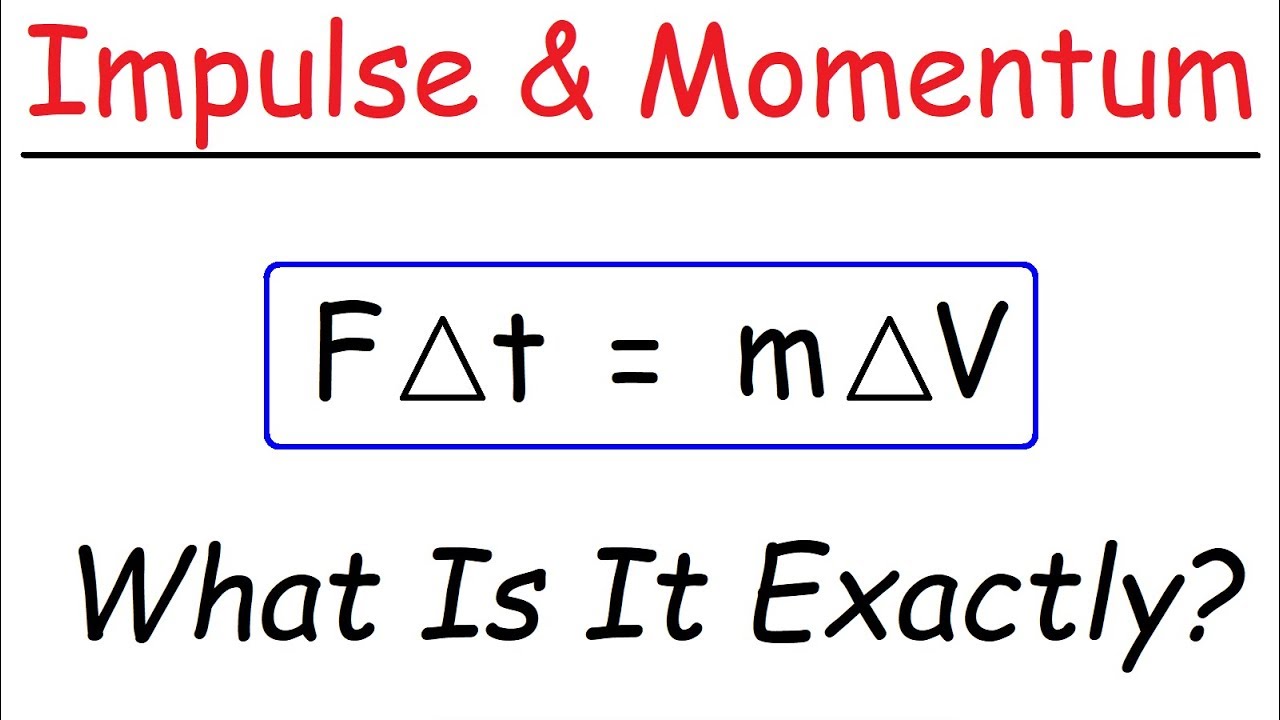
Introduction to Impulse & Momentum - Physics

Momentum and Impulse Explained

Impulse and Momentum Conservation - Inelastic & Elastic Collisions

GCSE Physics - Momentum Part 1 of 2 - Conservation of Momentum Principle #59

IGCSE Physics [Syllabus 1.6] Momentum