Calculator Techniques in Composition of Functions | Engr. Yu Jei Abat | #AbatAndChill
TLDRThis video tutorial delves into the art of calculating compositions of functions using both conventional and calculator-based techniques. It begins with a step-by-step guide on evaluating f(g(5)) for given functions f(x) and g(x), emphasizing the substitution process. The instructor then explores alternative methods, such as assigning intermediate values to a new variable, to simplify the process. The video also covers solving for f(g(x)) and iterated functions like f(f(f(f(1)))), demonstrating how to use a calculator to handle complex compositions efficiently. The tutorial concludes with an encouragement to subscribe for more educational content, making it an informative and engaging resource for students preparing for exams or studying function composition.
Takeaways
- 📚 The video discusses calculator techniques for evaluating the composition of functions, providing both conventional and calculator-based methods.
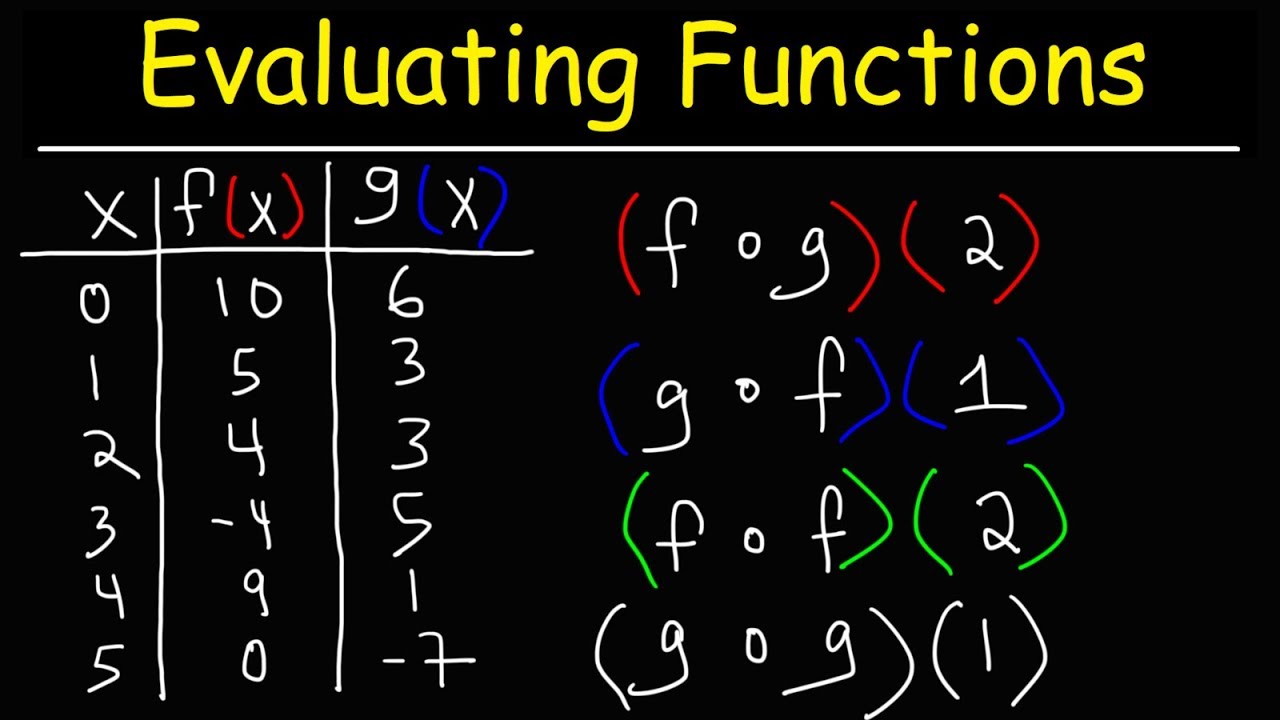
- 🔢 The first example demonstrates how to calculate \( f(g(5)) \) for given functions \( f(x) \) and \( g(x) \), emphasizing the process of substituting values step by step.
- 💡 A calculator is used to compute the value of \( g(5) \) first, and then the result is used as an input for \( f(x) \) to find \( f(g(5)) \).
- 📝 The script introduces an alternative method by assigning the inner function's result to a variable (e.g., y) and then substituting it into the outer function for a quicker calculation.
- 🔄 The process of changing variables (from x to y) simplifies the substitution process in the calculator and helps avoid confusion.
- 📉 In the second problem, the composition \( f(g(x)) \) is evaluated without specific values, resulting in an expression that can be assigned to any x value for further computation.
- 📝 The script shows how to use the calculator to solve for \( f(g(x)) \) by first finding \( g(x) \) and then substituting its result into \( f(x) \).
- 🎯 The third example involves nested function compositions, such as \( f(f(f(f(1)))) \), where the same function is applied repeatedly to its own output.
- 🔢 The video explains how to use the calculator to iteratively input and compute the result of the nested function until the final value is obtained.
- 📈 The script also suggests using a variable (like y) to store intermediate results, streamlining the process of evaluating nested functions.
- 👍 The video encourages viewers to like, share, and subscribe for more educational content on calculator techniques and related topics.
Q & A
What is the main topic of the video?
-The main topic of the video is calculator techniques for the composition of functions.
What are the functions given in problem number one?
-In problem number one, the function f(x) is given as 2x^3 + 3x^2 - 7x + 5, and the function g(x) is given as 3x^2 - 11x + 2.
What is the process to evaluate f(g(5)) as described in the video?
-To evaluate f(g(5)), first compute g(5) by substituting x with 5 in the g(x) function. Then, take the result from g(5) and substitute it as x in the f(x) function.
What is the result of g(5) in the video?
-The result of g(5) is 22, which is then used as the input for the function f(x).
Can you explain the alternative method mentioned in the video for evaluating compositions of functions?
-The alternative method involves assigning the inner function (g(x) in this case) to a new variable, say y, and then substituting x in the outer function (f(x)) with y to simplify the process.
What is the purpose of changing the variable from x to y in the alternative method?
-Changing the variable from x to y helps to avoid confusion when substituting the result of the inner function (now stored as y) into the outer function.
What is the process for problem number two as described in the video?
-For problem number two, first evaluate g(x) by substituting x with the given value, and then substitute the result into f(x) to find f(g(x)).
What is the expression for f(g(x)) in problem number two?
-The expression for f(g(x)) in problem number two is 2x + 3, where x is substituted with the result of 3x + 2 from g(x).
How does the video demonstrate solving f(f(f(f(1))))?
-The video demonstrates solving f(f(f(f(1)))) by repeatedly substituting the result of f(x) back into the function f(x) four times, starting with x = 1.
What is the final result of f(f(f(f(1)))) as shown in the video?
-The final result of f(f(f(f(1)))) is one million four hundred ninety-nine thousand three hundred seventy-one.
What is the advice given at the end of the video for those who found it helpful?
-The advice given at the end of the video is to like, share, subscribe to the channel, and share the video with friends who are preparing for board exams or studying integration and correlation courses.
Outlines
🧮 Calculating Composite Functions Using a Calculator
This paragraph introduces the topic of calculating the composition of functions using both conventional methods and calculator techniques. The first problem involves evaluating f(g(5)) for given functions f(x) and g(x). The process involves first computing g(5), then substituting the result into f(x). The explanation includes a step-by-step guide on using a calculator to perform these operations, emphasizing the importance of entering values correctly and understanding the compositional nature of the functions.
🔍 Exploring Alternative Methods for Function Composition
The second paragraph delves into alternative methods for calculating composite functions, such as changing the variable from x to y to avoid confusion and simplify the process. It also discusses the importance of understanding the order of operations and the significance of substituting values correctly. The paragraph provides an example problem involving f(g(x)) and demonstrates how to solve it using a calculator, including assigning values to x and evaluating the resulting expressions.
🔢 Iterative Function Composition and Calculator Techniques
The third paragraph presents a more complex scenario of nested function composition, specifically f(f(f(f(x)))). It outlines the iterative process of substituting the result of one function into itself multiple times. The explanation includes a practical approach using a calculator, emphasizing the need for repeated input of values and careful tracking of each step's outcome. The paragraph also suggests using an alternative variable to streamline the process and avoid confusion.
📢 Conclusion and Encouragement for Further Learning
The final paragraph serves as a conclusion to the video script, encouraging viewers to apply the calculator techniques learned for function composition in their studies, particularly for board exams and integration courses. It invites viewers to like, share, and subscribe to the channel for more helpful content, highlighting the value of the video in aiding understanding and practical application of mathematical concepts.
Mindmap
Keywords
💡Calculator Techniques
💡Composition of Functions
💡Function Evaluation
💡Variable Substitution
💡Calculus Concepts
💡Nested Functions
💡Solving for X
💡Equation Solving
💡Algebraic Manipulation
💡Educational Content
Highlights
Introduction to calculator techniques for the composition of functions.
Explanation of how to effectively calculate the result of a composition of functions.
Demonstration of the process to evaluate f(g(5)) using given functions f(x) and g(x).
Step-by-step guide on substituting values into functions for composition calculations.
Using a calculator to compute g(5) before substituting into f(x).
Method of changing variables to avoid confusion during substitution, such as using y instead of x.
Alternative technique of directly substituting the result of g(5) into f(x).
Explanation of how to handle composition functions with the same variable x.
Illustration of calculating f(g(x)) for a given x value without specific numerical input.
Process of assigning a value to x and reverse engineering the choices for f(g(x)).
Using the calculator to solve for f(g(x)) with an example value of x.
Method to evaluate multiple compositions of the same function, such as f(f(f(f(1)))).
Technique of using another variable y to store intermediate results for repeated function compositions.
Calculating the result of nested function compositions step by step using the calculator.
Final result of the nested composition f(f(f(f(1)))) and its significance.
Encouragement to like, share, and subscribe for more educational content.
Invitation to share the video with friends preparing for exams or studying integration and correlation courses.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: