Sean Carroll, "The Biggest Ideas in the Universe: Space, Time, and Motion"
TLDRJasmine Parmley introduces Sean Carroll's book event at Harvard, where he discusses 'The Biggest Ideas in the Universe: Space, Time, and Motion'. Carroll, a theoretical physicist and popular science writer, dives into the depths of Einstein's general relativity, exploring the curvature of space-time as the essence of gravity. He explains the mathematical framework behind these concepts, highlighting the importance of equations in revealing the universe's mysteries, including the unexpected prediction of black holes. The talk concludes with an insightful Q&A session, touching on topics from quantum mechanics to the philosophy of science.
Takeaways
- 📚 Sean Carroll's new book 'The Biggest Ideas in the Universe: Space, Time, and Motion' aims to explain complex physics concepts in an accessible manner.
- 🔍 The event was hosted by Harvard Book Store and introduced by Cora Dvorkin, emphasizing the importance of science literature and community engagement.
- 🌌 Carroll discussed Einstein's field equation for general relativity, highlighting its significance in understanding the curvature of space-time as the essence of gravity.
- 📐 The lecture delved into the transition from classical mechanics, represented by Newton's laws, to the theory of relativity, which includes the concept of space-time geometry.
- 🕰 Carroll emphasized the universality of gravity and its experimental validation, such as the Apollo 15 moon gravity experiment with a hammer and a feather.
- 🧠 Einstein's realization that gravity could be seen as a feature of space-time geometry, rather than a force, was a pivotal moment in the development of general relativity.
- 📉 The Schwarzschild metric, a solution to Einstein's equation, describes the space-time geometry outside a spherical mass and is foundational in understanding gravitational lensing and black holes.
- 🌐 The concept of space-time and its curvature is central to understanding the large-scale structure of the universe and phenomena like gravitational waves.
- 🔮 The James Webb Telescope was mentioned as a tool for exploring the universe's evolution but not for testing fundamental physics principles.
- 🤔 The discussion touched on the philosophical implications of physics, including the nature of time, causality, and the possibility of time travel.
- 🌟 The event concluded with an emphasis on the synergy between physics and philosophy, suggesting that both are necessary for a comprehensive understanding of the universe.
Q & A
What is the main topic of Sean Carroll's new book 'The Biggest Ideas in the Universe: Space, Time, and Motion'?
-The main topic of Sean Carroll's new book is to explain not only the physical concepts but also the mathematical framework behind the fundamental ideas of space, time, and motion in a comprehensive and accessible way.
Why is the equation 'R mu nu - one-half r g mu nu equals 8 Pi g t mu nu' significant in the context of the presentation?
-This equation is significant as it represents Einstein's field equation for the curvature of space-time in general relativity, which is a central concept in Carroll's discussion about the biggest ideas in the universe.
What is the role of the Harvard Science Book Talk series mentioned by Jasmine Parmley?
-The Harvard Science Book Talk series aims to bring authors of recently-published science literature to the Cambridge community and beyond, fostering engagement with scientific ideas and authors.
Who introduced Sean Carroll at the event, and what is their professional background?
-Cora Dvorkin, an Associate Professor in Harvard's Physics Department and a theoretical cosmologist, introduced Sean Carroll at the event.
What is the importance of Newton's Second Law 'F equals ma' in classical mechanics?
-Newton's Second Law is central to classical mechanics as it establishes a precise and universal relationship between force, mass, and acceleration, which is essential for predicting the motion of objects.
What is the significance of the universality of gravity as discussed by Sean Carroll?
-The universality of gravity is significant because it implies that all objects accelerate in the same way under gravity, regardless of their individual characteristics. This principle was crucial for Einstein in developing his theory of general relativity.
What was the contribution of Hermann Minkowski to the understanding of relativity?
-Hermann Minkowski contributed to the understanding of relativity by proposing that space and time are not separate but unified into something called space-time, where the effects described by relativity are manifestations of the geometry of space-time.
How does the presentation by Sean Carroll relate to the audience's understanding of Einstein's theory of relativity?
-Carroll's presentation aims to deepen the audience's understanding of Einstein's theory of relativity by explaining the mathematical framework and the physical concepts in an accessible manner, focusing on the curvature of space-time and its implications.
What is the significance of the event being recorded by C-SPAN Book TV?
-The recording of the event by C-SPAN Book TV signifies the importance and the broad audience reach of the discussion on the biggest ideas in the universe, as it allows a wider viewership to access the insights shared during the event.
What is the role of the metric tensor 'G mu nu' in the context of general relativity?
-In the context of general relativity, the metric tensor 'G mu nu' encodes the geometry of space-time, capturing the information needed to calculate distances and the flow of time in the presence of matter and energy.
What does Sean Carroll suggest as a possible direction for future research in physics?
-Sean Carroll suggests that a deeper understanding of quantum mechanics might be necessary for making progress in quantum gravity, hinting at the need to reconcile general relativity with quantum mechanics.
Outlines
📚 Introduction and Event Overview
Jasmine Parmley welcomes everyone to the event on behalf of Harvard Book Store, Harvard University Division of Science, and the Harvard Library. She introduces the event featuring Sean Carroll presenting his new book 'The Biggest Ideas in the Universe: Space, Time, and Motion.' She also mentions housekeeping items, the recording by C-SPAN Book TV, and details about the book signing at Cabot Library.
👩🏫 Introduction of Sean Carroll by Cora Dvorkin
Cora Dvorkin, Associate Professor in Harvard's Physics Department, introduces Sean Carroll. She highlights Carroll's contributions to theoretical physics and his commitment to making complex physics accessible. She shares her personal experience with Carroll's work and introduces his new trilogy, starting with 'The Biggest Ideas in the Universe: Space, Time, and Motion.'
🌌 Sean Carroll Begins His Presentation
Sean Carroll thanks the organizers and the audience. He briefly mentions his background at Harvard and Johns Hopkins University. Carroll introduces his new book, the first in a trilogy, and decides to focus on Einstein's equation to provide a taste of the book's content. He clarifies the difference between the familiar equation E=mc² and the more complex Einstein's field equation.
🔬 Einstein's Equation and Its Significance
Carroll explains the Einstein field equation in detail, emphasizing its significance in general relativity. He discusses the components of the equation and its implications for understanding the curvature of space-time. Carroll connects this to classical mechanics, starting with Newton's Second Law, and highlights the precision and universality of physical laws.
🪐 Gravity and Classical Mechanics
Carroll elaborates on Newton's law of gravitation, explaining how force, mass, and acceleration relate. He describes the universal nature of gravity, where objects accelerate similarly under its influence, regardless of their composition. Carroll uses examples like the Apollo 15 experiment on the Moon to illustrate the uniformity of gravitational acceleration.
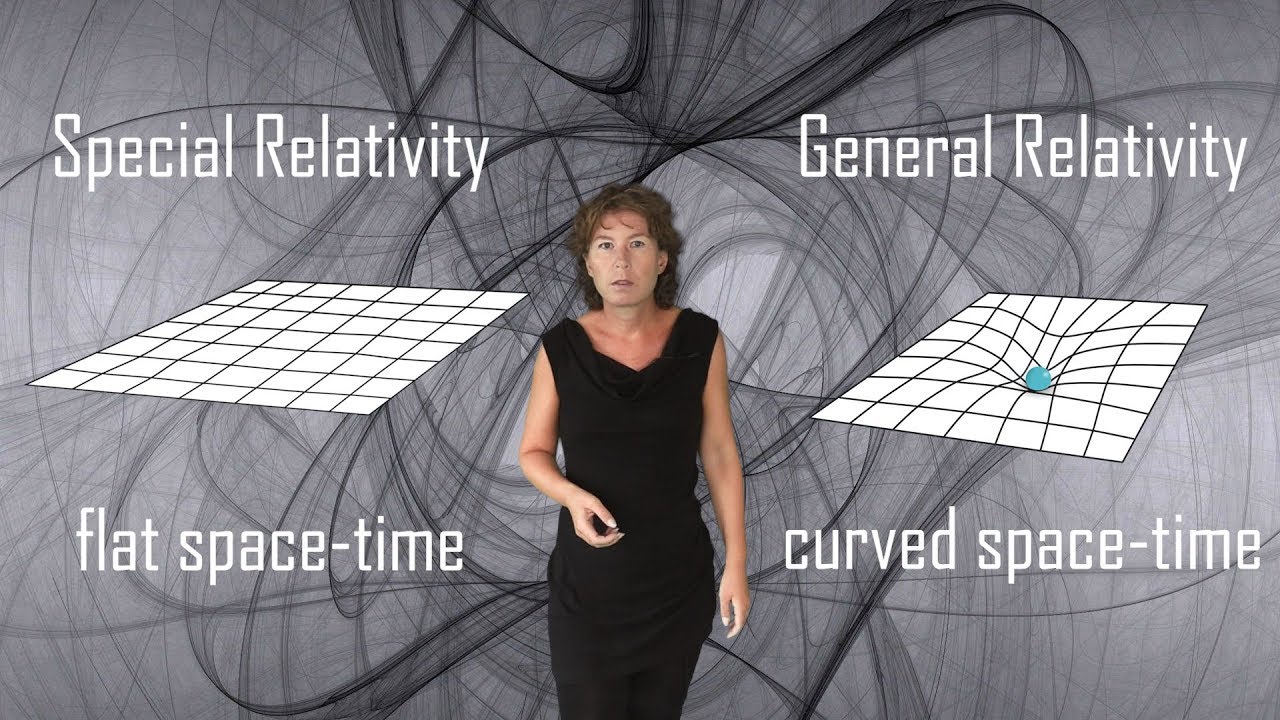
🔭 Einstein and the Development of Relativity
Carroll discusses Einstein's contributions to special and general relativity, contrasting them with classical mechanics. He introduces Minkowski's space-time concept and its impact on understanding relativity. Carroll highlights Einstein's initial resistance to Minkowski's ideas and his eventual acceptance, which led to the development of general relativity.
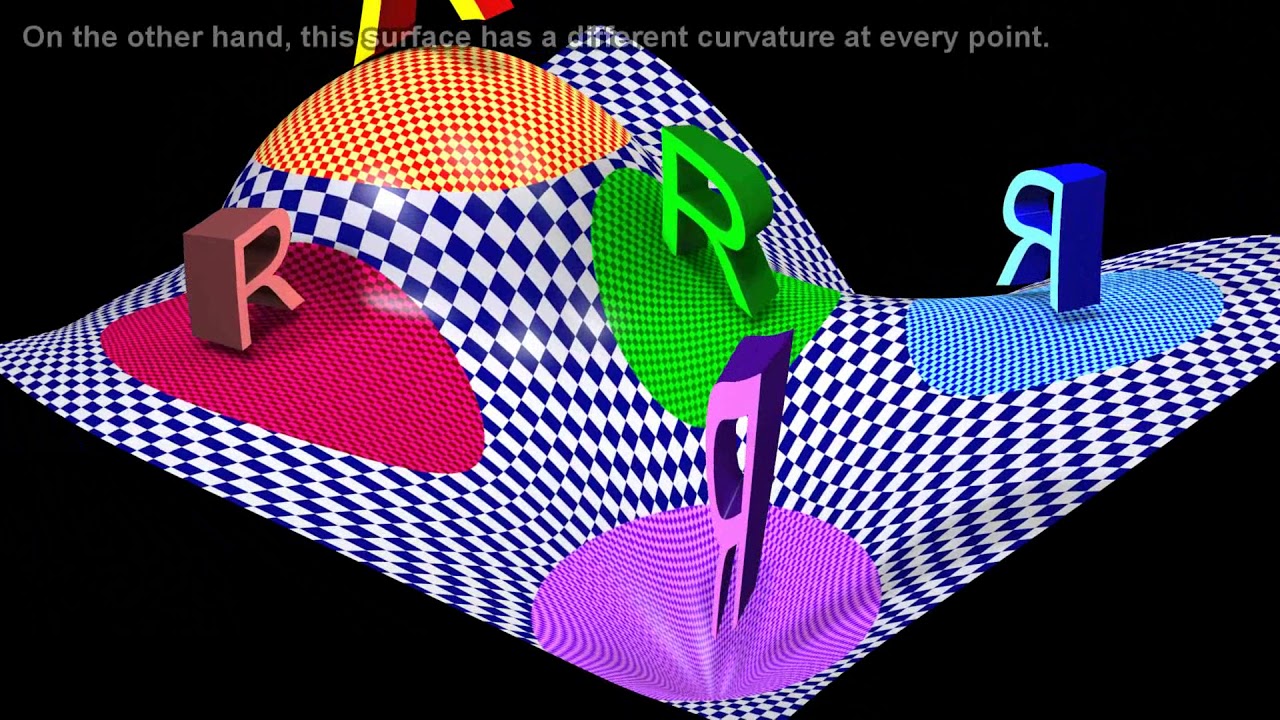
🌍 Non-Euclidean Geometry and Curved Space-Time
Carroll explains the history and significance of non-Euclidean geometry, developed by mathematicians like Riemann and Gauss. He describes how this new geometry allowed for the understanding of curved space-time, which is essential for general relativity. Carroll details the contributions of Riemann in generalizing the geometry of curved surfaces and spaces.
📐 The Mathematics of Space-Time
Carroll dives deeper into the mathematical framework of space-time, introducing the concept of the metric tensor. He explains how the metric tensor encodes the geometry of space-time and how Riemann's work laid the foundation for this understanding. Carroll uses simplified notation to describe the components of the metric tensor and their significance.
🎥 Time and Space Intertwined
Carroll uses the movie 'Interstellar' to illustrate the concept of time and space twisting into each other near a black hole. He explains how this phenomenon is accurately depicted in the movie through advanced computer simulations. Carroll emphasizes the importance of understanding these concepts in theoretical physics and their real-world implications.
🧮 The Riemann Tensor and Curvature
Carroll introduces the Riemann tensor, a mathematical tool that describes the curvature of space-time. He explains how the Riemann tensor is derived from the metric tensor and its role in general relativity. Carroll discusses the complexity of the tensor and its components, emphasizing its significance in understanding the geometry of space-time.
⚖️ Einstein's Equation for Gravity
Carroll explains how Einstein's field equation for gravity relates the curvature of space-time to the energy-momentum tensor. He describes the process of deriving the equation and its components, including the Ricci tensor and curvature scalar. Carroll highlights the significance of this equation in general relativity and its implications for our understanding of gravity.
🌠 Solving Einstein's Equation
Carroll discusses the challenges of solving Einstein's field equation and the contributions of Karl Schwarzschild. He explains the Schwarzschild solution for a spherically symmetric mass and its implications for understanding black holes. Carroll emphasizes the importance of this solution in predicting and understanding the behavior of objects in strong gravitational fields.
🕳️ Black Holes and Einstein's Legacy
Carroll explores the concept of black holes, which emerged from the solutions to Einstein's equation. He describes how black holes were not initially predicted by Einstein but were later understood through the mathematical implications of his theory. Carroll highlights the ongoing research and discoveries related to black holes and their significance in modern astrophysics.
🔄 The Nature of Causality
Carroll addresses questions about causality and its role in physics. He explains his view that causality is not fundamental but emerges from the higher-level descriptions of physical laws. Carroll connects this idea to the second law of thermodynamics and the increase of entropy, emphasizing the difference between microscopic and macroscopic descriptions.
🌌 Understanding the Universe's Age
Carroll answers questions about the age of the universe and how it is measured. He explains the concept of elapsed time in cosmology and the significance of the 13.8 billion-year figure. Carroll clarifies that this measurement is consistent across most galaxies due to their relatively slow movement compared to the speed of light.
🌀 Quantum Mechanics and Space-Time
Carroll discusses the relationship between quantum mechanics and general relativity. He acknowledges the challenges of reconciling the two theories and suggests that a better understanding of quantum mechanics might be key to solving these issues. Carroll hints at the topics covered in the next volume of his book series, focusing on quantum mechanics.
🧠 Interdisciplinary Approaches
Carroll emphasizes the importance of interdisciplinary approaches in advancing scientific understanding. He highlights the synergy between physicists and mathematicians in developing general relativity and suggests that collaboration between different fields can lead to significant breakthroughs. Carroll also discusses the role of philosophy in complementing scientific research.
🕰️ Reflections on Time Travel and Parallel Universes
Carroll briefly touches on the concepts of time travel and parallel universes, topics he explored in his book 'From Eternity to Here.' He explains that while general relativity allows for theoretical considerations of time travel, practical implementation remains speculative and unlikely. Carroll emphasizes the complexity and fascinating nature of these ideas.
📊 Information in the Riemann and Ricci Tensors
Carroll addresses a question about the loss of information when transitioning from the Riemann tensor to the Ricci tensor in Einstein's equation. He explains that while not all components are directly used, the remaining components are related through derivatives, ensuring the equation's consistency. Carroll also mentions gravitational waves as a manifestation of this relationship.
🧐 Philosophical Perspectives in Physics
Carroll discusses the interplay between physics and philosophy, advocating for a holistic approach that incorporates philosophical thinking into scientific research. He highlights the importance of philosophical insights in addressing foundational questions in physics and encourages scientists to engage with philosophical concepts to enrich their understanding.
🎓 Conclusion and Future Directions
Carroll concludes his talk by emphasizing the value of equations in physics for their precision and universality. He encourages continued exploration and understanding of these equations to uncover new insights about the universe. The event ends with a round of applause and an invitation to join the book signing and refreshments at Cabot Library.
Mindmap
Keywords
💡General Relativity
💡Space-time
💡Newton's Second Law
💡Einstein's Equation
💡Quantum Mechanics
💡Metric Tensor
💡Riemann Tensor
💡Energy-Momentum Tensor
💡Black Hole
💡Gravitational Waves
💡Cosmology
Highlights
Introduction of Sean Carroll's new book 'The Biggest Ideas in the Universe: Space, Time, and Motion'.
Carroll's commitment to making complex physics concepts accessible to everyone.
Explanation of Einstein's field equation for the curvature of space-time in general relativity.
The significance of Newton's Second Law and its universality in classical mechanics.
Newton's law of gravity and its implications for understanding the force of gravity.
Einstein's realization that gravity is an intrinsic feature of space-time geometry.
The role of Minkowski in unifying space and time into a single continuum known as space-time.
Introduction to the concept of geometry in special relativity and its relation to the proper time.
Einstein's struggle and eventual success in reconciling Newtonian gravity with relativity.
The development of the metric tensor as a way to encode the geometry of space-time.
The invention of non-Euclidean geometry and its impact on our understanding of space-time.
Riemann's contribution to describing the geometry of curved spaces with his namesake tensor.
Einstein's field equations derived from the curvature of space-time and their implications.
Schwarzschild's solution to Einstein's equation and its prediction of black holes.
The philosophical implications of general relativity on our understanding of time and causality.
Carroll's views on the future of physics, particularly the unification of general relativity and quantum mechanics.
The importance of equations in physics for revealing deeper truths about the universe beyond our initial understanding.
Transcripts
Browse More Related Video
Einstein's Field Equations of General Relativity Explained

The Paradoxes of Time Travel

Brian Greene and Leonard Susskind: Quantum Mechanics, Black Holes and String Theory
How we know that Einstein's General Relativity can't be quite right

Carlo Rovelli: The Man Expanding Our Understanding of the Universe | UNFILTERED

Einstein's Universe: Understand Theory of General Relativity
5.0 / 5 (0 votes)
Thanks for rating: