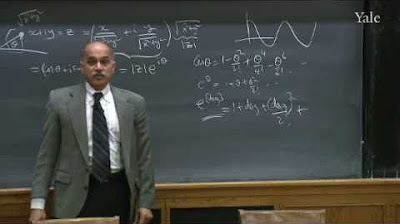Lecture 23: Owls, Rats, Waves and Guitars
TLDRThis lecture explores the application of differential equations to model complex real-world phenomena. It starts with a predator-prey model, illustrating how populations of wood rats and spotted owls interact and fluctuate over time, governed by a set of coupled differential equations. The lecture then transitions to the physical world, specifically the vibration of a guitar string, and derives the wave equation that describes its motion. By analyzing the string's tension and shape, the wave equation is established, leading to solutions that explain the rich harmonics heard when a string is plucked. The lecture effectively demonstrates how differential equations can provide insights into both biological systems and physical vibrations.
Takeaways
- 📚 The lecture discusses differential equations and their application in describing physical and biological phenomena, such as the motion of a dropped ball and population growth models.
- 🧩 The solutions to differential equations often represent functions of one variable, typically time, which describe changes in systems like a ball's position or population size over time.
- 🕊️ The lecture introduces a model for two interacting species, specifically a predator-prey relationship between northern spotted owls and wood rats, which are used to illustrate more complex differential equations.
- 📉 The model assumes that without predators, prey populations grow exponentially, and without prey, predator populations decline exponentially due to lack of food.
- 🔄 The interaction between the two species is modeled by equations that account for the rate of change in each population based on the product of their numbers, reflecting the ecological impact of predation.
- 📈 The lecture explains how to visualize the dynamics of the predator-prey model using a vector field or direction field, which shows the rate of change for both populations at any given point.
- 🔢 The populations' interaction results in a cyclical pattern where the prey and predator populations increase and decrease in a predictable cycle, which can be traced by following the vector field.
- 🎶 The second part of the lecture shifts focus to the application of differential equations in understanding the vibration of a musical instrument string, such as a guitar.
- 🎵 The motion of a vibrating string is described by a function of two variables, where the displacement of the string is given by \( u(x, t) \), with \( x \) representing position along the string and \( t \) representing time.
- 🎹 The wave equation derived for the vibrating string relates the second derivative of the string's displacement with respect to time to the second derivative with respect to position, influenced by the string's tension and mass.
- 🎷 Solutions to the wave equation, such as sine and cosine functions, represent different vibration modes of the string, which correspond to different musical notes and overtones, contributing to the richness of the instrument's sound.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the application of differential equations to model physical and biological phenomena involving more than one variable, specifically focusing on predator-prey relationships and vibrating strings.
How are differential equations used to describe the motion of a dropped ball?
-Differential equations are used to describe the motion of a dropped ball by taking into account the force acting on the ball and its acceleration as it falls, which allows us to determine the function that tells us where the ball is at each moment.
What is the basic assumption made about the growth of wood rat population in the absence of owls?
-The basic assumption made about the growth of the wood rat population in the absence of owls is that they would grow exponentially due to the abundance of resources.
How does the presence of owls affect the wood rat population in the model?
-In the model, the presence of owls affects the wood rat population by causing a decline in their numbers, as owls eat the wood rats, which is reflected in the differential equation by a negative interaction term.
What is the Lotka-Volterra model and how does it relate to the lecture's content?
-The Lotka-Volterra model is a set of differential equations that describe the dynamics of predator-prey (or herbivore-plant) interactions. It is related to the lecture's content as it is used to model the relationship between the populations of wood rats and owls.
What is the significance of the Hudson Bay trading company records in the context of the lecture?
-The Hudson Bay trading company records are significant because they provide historical data on the populations of Canadian lynxes and snowshoe hares, which show an alternating pattern of growth and decline, verifying the predictions made by the predator-prey model.
How does the lecture connect the concept of differential equations to the study of vibrating strings?
-The lecture connects the concept of differential equations to the study of vibrating strings by discussing how the motion of a string can be described using a function of two variables and how the wave equation can be derived from the physical properties of a vibrating string.
What is the physical interpretation of the second derivative of the string's position with respect to time?
-The physical interpretation of the second derivative of the string's position with respect to time is the acceleration of the string's vertical position, which is associated with the force acting on the string.
What are the boundary conditions for the vibrating guitar string in the lecture?
-The boundary conditions for the vibrating guitar string in the lecture are that the endpoints of the string are always fixed, meaning the string's value at the beginning and the end is always zero for all time.
How does the lecture explain the rich sound of a guitar note?
-The lecture explains the rich sound of a guitar note by describing it as a combination of the fundamental frequency and its multiples, which are produced by the different modes of vibration of the string.
Outlines
📚 Introduction to Differential Equations in Physical and Biological Phenomena
This paragraph introduces the concept of differential equations and their applications in describing physical and biological phenomena. The lecturer discusses how these equations can model scenarios such as a ball falling under gravity and population growth in biology. The focus is on how differential equations reflect the rate of change with respect to time, and the solutions sought are functions of a single variable, typically time. The lecture aims to extend this idea to more complex situations involving multiple variables, setting the stage for the exploration of differential equations in more intricate contexts.
🐦 Predator-Prey Model Using Differential Equations
The second paragraph delves into the application of differential equations to model the interaction between two species, specifically a predator-prey relationship. The example given is that of a northern spotted owl and wood rats, where the owls' diet primarily consists of wood rats. The lecturer explains the process of creating a mathematical model to describe how the populations of these two species change over time. The model involves two differential equations, one for each species, taking into account factors such as growth, predation, and resource availability. The goal is to find functions that represent the populations of wood rats and owls at any given time.
📉 Developing a Mathematical Model for Population Dynamics
In this paragraph, the lecturer simplifies the concept of population growth to create a basic model. It starts with the assumption that wood rats would grow exponentially if there were no owls, and owls would decline exponentially if there were no wood rats. The model then incorporates the interaction between the two species, where the presence of owls causes a decline in the wood rat population, and the availability of wood rats allows the owl population to grow. The paragraph introduces two differential equations that describe these dynamics, highlighting the interdependence of the two species' populations.
📈 Visualizing Population Dynamics with Vector Fields
The lecturer introduces the concept of a vector field or direction field to visualize the changing populations of wood rats and owls. By plotting the rate of change of each population (dw/dt for wood rats and ds/dt for owls) on a plane, with wood rat population on the horizontal axis and owl population on the vertical axis, the讲师 creates a visual representation of how the populations interact. At each point on the plane, an arrow is drawn to represent the direction and magnitude of change for both populations. This visual tool helps to understand the cyclical nature of the predator-prey relationship and how the populations fluctuate over time.
🎶 Transition to a Musical Instrument: The Vibrating String
This paragraph transitions from the biological context to a physical one, focusing on the motion of a vibrating string, such as that of a guitar. The lecturer aims to describe the movement of the string to understand how it produces sound. The paragraph sets the stage for the exploration of differential equations in the context of a vibrating string, which is a function of two variables: position along the string and time. This marks a shift from the previous examples, which involved single-variable functions.
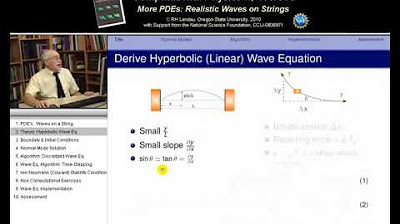
🎵 Deriving the Wave Equation for a Vibrating String
The lecturer begins to derive the wave equation for a vibrating string, starting with the observation that the motion of the string is influenced by the tension and the curvature of the string at any given point. By considering the forces acting on a small segment of the string, the讲师 relates the upward force to the second derivative of the string's position with respect to its spatial variable (x). Newton's second law of motion is then invoked to connect this force to the second derivative with respect to time (t), leading to the wave equation. The讲师 also mentions boundary conditions, such as the fixed endpoints of a guitar string, which are essential in solving the wave equation.
🎼 Harmonic Analysis of a Vibrating String and Musical Implications
In this final paragraph, the lecturer explores the solutions to the wave equation for a vibrating string, specifically for a string of length pi. The solutions involve sine and cosine functions, which represent different vibrational modes of the string. Each mode corresponds to a harmonic of the fundamental frequency, and the lecturer explains how these harmonics contribute to the rich sound of a musical note. The paragraph concludes with a demonstration of how placing a finger on the string at certain multiples of its length can produce different notes, illustrating the practical application of the wave equation in understanding musical instruments.
Mindmap
Keywords
💡Differential Equations
💡Physical World
💡Biological Phenomena
💡Population Growth
💡Predator-Prey Relationship
💡Exponential Growth
💡Vibrating String
💡Wave Equation
💡Partial Differential Equations
💡Fundamental Frequency
💡Harmonic
Highlights
Introduction to differential equations and their applications in describing physical and biological phenomena.
Differential equations can model scenarios like a falling ball and population growth, represented as functions of a single variable, typically time.
Lecture focus on differential equations involving more than one variable to reflect complex real-world phenomena.
Development of the derivative and integral concepts from simple to more complex scenarios, such as functions of multiple variables.
Modeling the interaction of two species, specifically a predator-prey relationship between northern spotted owls and wood rats.
Assumption of exponential growth for wood rats in the absence of predators (owls).
Modeling the decline of the owl population without their primary food source, the wood rats, using an exponential decay function.
Incorporating the interaction between owls and wood rats into differential equations to reflect the impact on population changes.
Visualizing population dynamics through a vector field, illustrating the rate of change for both species.
The cyclical pattern of population changes in predator-prey models, leading to a stable point or cyclic pattern.
Verification of predator-prey models through historical data from the Hudson Bay trading company on lynxes and snowshoe hares.
Transition to a new topic: using differential equations to describe the motion of a vibrating string, such as a guitar string.
Description of a vibrating string as a function of two variables: position along the string (x) and time (t).
Derivation of the wave equation for a vibrating string, relating the second derivative with respect to time and position.
Solutions to the wave equation for a string of length pi, involving sine and cosine functions.
Physical interpretation of the wave equation solutions, explaining the different vibrations and musical notes produced by a string.
Understanding of musical tones as combinations of fundamental frequencies and their multiples, enriching the sound of a guitar.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: