History of Maxwell's Equations #1: Gauss' Law
TLDRThis script recounts the historical development of Maxwell's equations, starting with Richard Feynman's admiration for Maxwell's work and the gaps in Feynman's own lectures. It delves into Coulomb's experiments leading to his law, Faraday's concept of electric lines of force and dielectrics, and Maxwell's mathematical interpretation of these ideas. The narrative follows Maxwell's evolution of his theories, including the introduction of displacement current and the refinement of Gauss's law. It highlights the contributions of scientists like William Rankine, William Thompson, and Oliver Heaviside, who helped shape the understanding of electromagnetism and the modern form of Maxwell's equations.
Takeaways
- 📚 The Feynman Lectures in Physics, started by Richard Feynman in the late 1950s, are considered a gold standard in physics education and continue to inspire physics teaching today.
- 🧲 Richard Feynman admired Maxwell's laws and considered Maxwell's discovery of the laws of electrodynamics as the most significant event of the 19th century, even more so than the American Civil War.
- 🔋 Coulomb's Law was developed by Charles-Augustin de Coulomb in the 1780s after observing the effects of static electricity on a sensitive magnetic compass; he found that electrical forces depend on the charges and inversely proportional to the square of the distance between them.
- 🎓 Michael Faraday was influenced by Coulomb's work and conducted experiments that led to the concept of electric field lines and the discovery of dielectrics, which are insulating materials that can become polarized in an electric field.
- 🛡️ Faraday's experiments with a metal cage, now known as a Faraday cage, demonstrated that a metal enclosure can shield the interior from external electric fields.
- 🌐 James Clerk Maxwell, a Scottish physicist, used the concept of 'molecular vortices' to model electric and magnetic fields and developed a set of equations that describe electromagnetism, including what is now known as Gauss's law.
- 📈 Maxwell's work on 'Physical Lines of Force' in 1861-1862 refined his earlier ideas, providing a physical meaning to the quantity of electric current, which he renamed 'displacement', and related it to the properties of dielectrics.
- 📚 Maxwell's 1864 paper introduced the concept of 'electric elasticity', which was later renamed 'permittivity' by Oliver Heaviside, to describe the relationship between the electric field and the displacement field in a dielectric.
- 🌟 Maxwell's equations, including Gauss's law, were foundational in explaining light as an electromagnetic wave and have had profound implications for the progress of science.
- 🔍 The script also hints at further exploration of the historical development of Maxwell's equations, the role of quaternions, and the contributions of other scientists like Heaviside, Hamilton, and Hertz in future content.
Q & A
What was the concern of the faculty at Cal Tech in the late 1950s regarding their undergraduate science curriculum?
-The faculty at Cal Tech were concerned that their undergraduate science curriculum wasn't keeping up with the exciting new developments in physics, including the discoveries made by Richard Feynman.
Why were the Feynman Lectures on Physics considered the gold standard of physics education?
-The Feynman Lectures on Physics were considered the gold standard of physics education because they were a compilation of beloved and influential lectures given by Richard Feynman, a renowned physicist and excellent teacher, which were immediately turned into a book.
What did Richard Feynman believe to be the most significant event of the 19th century?
-Richard Feynman believed that the most significant event of the 19th century was Maxwell's discovery of the laws of electrodynamics, considering it more impactful than even the American Civil War.
What was the shortcoming that Feynman admitted was missing from his lectures on electricity and magnetism?
-Feynman admitted that the historical experimental development was missing from his lectures on electricity and magnetism, and he suggested that this gap could be filled by reading supplementary materials or engaging in laboratory work.
What was Charles-Augustin de Coulomb's contribution to the understanding of electrical forces?
-Charles-Augustin de Coulomb developed a highly sensitive measuring device called the atorsional balance or twisting scale, which he used to experimentally determine that electrical repulsion and attraction forces are proportional to the inverse of the square of the distance between charges and also depend linearly on the charges.
How did Michael Faraday's work on electric lines and dielectrics build upon Coulomb's findings?
-Michael Faraday, inspired by Coulomb's work, discovered electric lines and dielectrics. He conceptualized that charged objects emit lines of force, and these lines could explain the behavior of electric fields, leading to the development of the Faraday cage and the understanding of how charges distribute on the surface of conductors.
What is the significance of the Faraday cage in the context of electric fields?
-The Faraday cage, a concept developed by Michael Faraday, demonstrates the principle of静电感应 (static induction). It shows that a metal cage can shield its interior from external electric fields, protecting anything inside from the effects of the field.
What was James Clerk Maxwell's approach to understanding and modeling Faraday's 'Lines of Force'?
-James Clerk Maxwell used a mathematical approach to model Faraday's 'Lines of Force'. He conceptualized these lines as fine tubes of variable section carrying an incompressible fluid, allowing him to use fluid dynamics to represent the intensity and direction of the electric force at any point.
How did Maxwell's initial model of 'molecular vortices' differ from his later model in 'On Physical Lines of Force'?
-Maxwell's initial model used the concept of tubes of incompressible fluids to represent electric lines of force. In his later work, 'On Physical Lines of Force', he shifted to a model of 'molecular vortices', which was more aligned with the then-modern atomic theory and allowed him to give a physical meaning to the quantity of electric current, renaming it as 'displacement'.
What is the modern interpretation of Maxwell's 'displacement current' in the context of Gauss's law?
-In the modern interpretation, Maxwell's 'displacement current' is understood as the change in the electric displacement field through a given surface, which is related to the charge enclosed by that surface. This concept is crucial in Gauss's law, where it accounts for the accumulation of charge within a given volume.
How did Oliver Heaviside contribute to the modern formulation of Maxwell's equations?
-Oliver Heaviside contributed by simplifying and reformulating Maxwell's equations into a more compact and mathematically elegant form known as the 'quaternion' form. He also introduced the concept of 'permittivity', which is the ratio of the displacement field to the electric field, making the equations more intuitive and easier to work with.
Outlines
📚 Introduction to Feynman's Lectures and Coulomb's Influence
The script begins with a tribute to Richard Feynman, a renowned physicist and educator, who was asked by Cal Tech to teach their revamped undergraduate physics program due to his excellent teaching skills and his concern about the curriculum's outdatedness. His lectures were recorded and later compiled into 'The Feynman Lectures in Physics,' which became a benchmark in physics education. The narrator mentions Feynman's admiration for Maxwell's laws and his acknowledgment of the lack of historical context in his lectures on electromagnetism. This leads to the narrator's decision to create a video series exploring the history behind Maxwell's equations, starting with Coulomb's law and its impact on subsequent scientific developments.
🧲 Coulomb's Law and Early Electromagnetic Experiments
This section delves into the historical experiments of Charles-Augustin de Coulomb in the 1780s. Initially, Coulomb's sensitive magnetic compass was affected by static electricity, prompting him to investigate the potential of this phenomenon. He developed the torsion balance, an exquisitely sensitive measuring device, and used it to study electric repulsion. Coulomb discovered that the electrical repulsion force is inversely proportional to the square of the distance between charges, a principle he declared as fundamental to electricity. He also studied attractive forces and found a similar inverse-square relationship. Coulomb's work laid the groundwork for understanding electric forces and charge distribution, which influenced future scientists like Michael Faraday.
🌐 Faraday's Discovery of Electric Lines and Dielectrics
The narrative then shifts to Michael Faraday in 1836, who was inspired by Coulomb's work, particularly his findings on charge distribution. Faraday, fresh from his discovery of magneto-electric induction, conducted experiments to further explore Coulomb's laws. He built a large copper cube to test the distribution of electric charges and discovered the shielding effect, which led to the concept of the Faraday cage. Faraday also introduced the idea of electric lines of force, visualizing the electric field around charged objects. He theorized that these lines represented both the direction and intensity of the electric force, and that conductors and insulators (which he renamed dielectrics) behaved differently in response to these lines of force. Faraday's experiments and theories significantly advanced the understanding of electromagnetism.
🔗 Maxwell's Interpretation of Faraday's Lines of Force
The script continues with the story of James Clerk Maxwell, who in 1854, sought to understand and build upon Faraday's work. Maxwell, with a strong mathematical background, recognized the mathematical essence of Faraday's conceptual methods. He set out to translate Faraday's ideas into mathematical language. Maxwell's initial approach was to conceptualize electric lines of force as tubes carrying an incompressible fluid, using fluid dynamics to model the electric force's variation with distance. He then introduced the concept of electric tension, equating it to voltage or potential in static electricity, thus connecting different phenomena within the field of electromagnetism.
🌌 Maxwell's Development of Electromagnetic Theory
Maxwell's work on Faraday's lines of force led him to develop a comprehensive theory of electromagnetism. He used the concept of tubes to represent the intensity of the electric field and introduced the idea of surfaces of equal pressure, which corresponded to equipotential surfaces in the electric field. Maxwell equated the electric tension to the potential in static electricity and derived an equation for the pressure from a single source in a uniform medium, which mirrored the modern definition of potential from a point charge. His work laid the foundation for understanding electric fields and potential, and he began to formulate what would later be known as Maxwell's equations.
🔧 Maxwell's Refinement of Gauss's Law and Molecular Vortices
In his 1861 to 1862 papers, Maxwell refined Gauss's law, introducing a physical model of the atom based on molecular vortices. This model helped him give a physical meaning to the quantity of electric current, which he renamed 'displacement.' Maxwell's revisions to Gauss's law included a redefinition of the constant relating the electric field to the displacement field, influenced by the nature of the dielectric. He also made changes to the notation and the sign convention, which were later adopted by Oliver Heaviside. Maxwell's work during this period solidified the understanding of electric fields and their interaction with matter.
📈 Maxwell's Equations and the Concept of Electric Elasticity
Maxwell's 1864 paper introduced the concept of 'electric elasticity' to describe the interaction between electric displacement and the electric field within a dielectric material. He proposed that the electric field is inversely proportional to this elasticity, which is dependent on the dielectric constant. This paper also saw Maxwell simplifying the relationship between the electric field and the displacement field, reverting to a constant K and removing the four pi factor. His work in this paper further developed the understanding of electromagnetic fields and their properties, leading to the modern form of Maxwell's equations.
🎥 Conclusion and Invitation to Further Exploration
The script concludes with an invitation to the audience to delve deeper into the history and development of Maxwell's equations. It hints at the involvement of other notable scientists like William Rankine, William Thompson (Lord Kelvin), Carl Frederick Gauss, and Oliver Heaviside. The narrator also mentions the mathematical functions called quaternions and the influence of Hamilton, Tate, and Hertz on the field of electromagnetism. The audience is encouraged to subscribe for more content and to visit the narrator's website for additional resources, including a book on the subject and information about an audiobook version.
📘 Promotion of Resources and Upcoming Book
In the final paragraph, the narrator promotes their personal website, www.kathylovesphysics.com, where interested viewers can find the full script of the video, including citations, and learn more about the narrator's new book, 'The Lightning Tamers,' which is available for pre-order. The website also hosts a GoFundMe campaign for an audiobook version of the book. The narrator thanks their patrons and ends with a reminder for viewers to stay safe and curious.
Mindmap
Keywords
💡Richard Feynman
💡Maxwell's laws
💡Coulomb's law
💡Electric field
💡Faraday cage
💡Dielectric
💡Gauss's law
💡Displacement current
💡Electromagnetic field
💡Permittivity
💡Quaternions
Highlights
In the late 1950s, Cal Tech revamped their undergraduate science curriculum, leading to Richard Feynman's iconic lectures on physics.
Feynman's lectures were recorded and compiled into a book, setting a gold standard for physics education.
Feynman admired Maxwell's laws, considering them the most significant event of the 19th century.
Feynman acknowledged a missing element in his lectures: the historical experimental development.
Charles-Augustin de Coulomb's sensitive magnetic compass led to the discovery of electrical forces.
Coulomb's torsion balance was the world's most precise measuring device at the time.
Coulomb's law states that electrical repulsion force is proportional to one over the distance squared.
Coulomb determined that the attractive force of opposite charges follows the same inverse-square relationship.
Coulomb found that the electric force depends linearly on the charges, measured in units now named after him.
Coulomb's experiments led to the understanding that electric fluid is only diffused over the surface of conductive objects.
Michael Faraday was inspired by Coulomb's work to discover electric lines and dielectrics.
Faraday's experiments with a large cube demonstrated the shielding effect of a Faraday cage.
Faraday theorized that all charged objects emanate lines of electric force, influencing the electric field.
Faraday introduced the concept of dielectrics and their effect on the electric field.
Faraday's work on specific inductive capacity led to the measurement of the dielectric constant.
James Clerk Maxwell sought to combine Faraday's ideas with mathematical rigor.
Maxwell's 'Lines of Force' papers modeled electric force using the concept of incompressible fluid tubes.
Maxwell derived Gauss's law connecting the divergence of the electric field to charge density.
Maxwell's work on 'Physical Lines of Force' introduced the concept of displacement current.
Maxwell's 1864 paper established the relationship between electric field and displacement field, introducing 'electric elasticity'.
Oliver Heaviside later redefined Maxwell's 'electric elasticity' as 'permittivity' for clearer physical interpretation.
The permittivity of free space is a constant that accounts for the reduction of electric field in a vacuum.
Feynman's lectures on Maxwell's equations highlighted the form and significance of Gauss's law.
Transcripts
Browse More Related Video

Maxwell's Equations Explained: Supplement to the History of Maxwell's Eq.
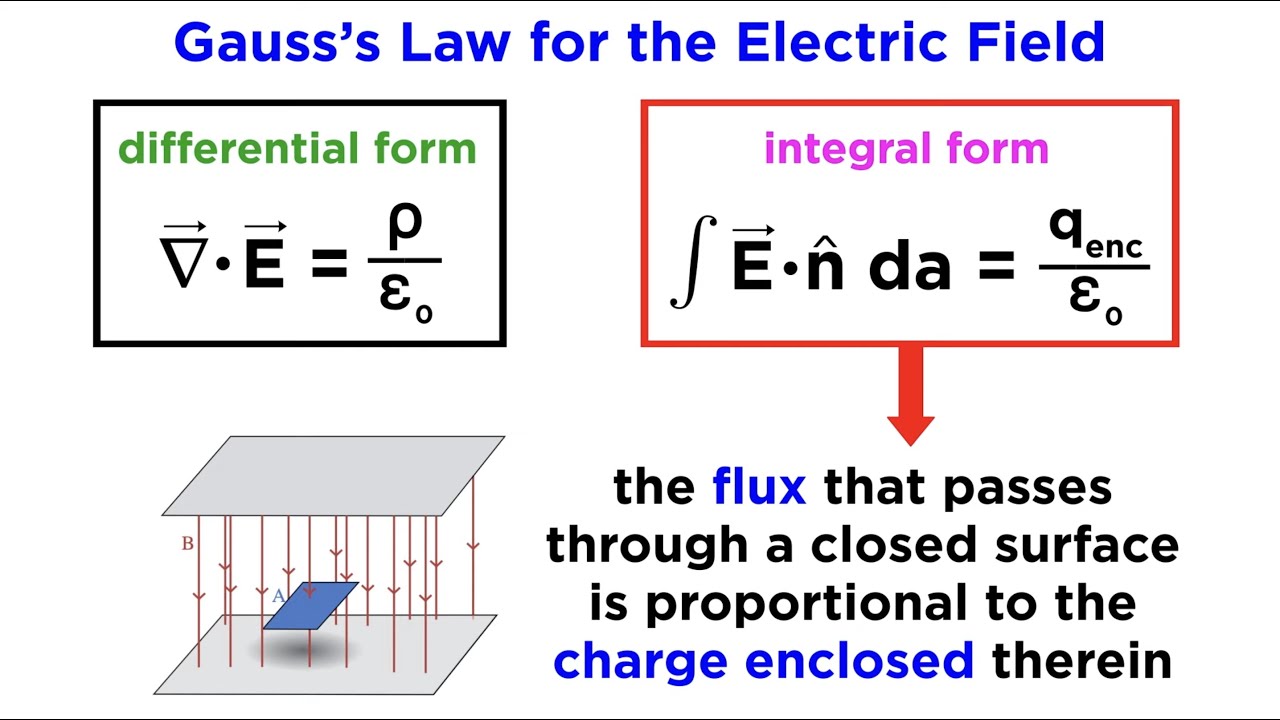
Maxwell’s Equations Part 1: Gauss’s Law for the Electric Field

How Maxwell's Equations (and Quaternions) Led to Vector Analysis

James Clerk Maxwell - A Sense of Wonder - Documentary

Maxwell's Equations: Crash Course Physics #37

Special Relativity | Lecture 8
5.0 / 5 (0 votes)
Thanks for rating: