Oxford Maths Admissions Interview Question with @blackpenredpen
TLDRIn this engaging video, Steve from 'Black Pen Red Pen' is invited as a special guest to Tom's channel, where they delve into a fascinating mathematical paradox known as Gabriel's Horn. Steve, a calculus enthusiast, shares insights into his channel's content, which includes tackling complex calculus problems and Oxbridge interview questions. The video features an in-depth exploration of Gabriel's Horn, a shape with an infinite surface area but finite volume. Through rigorous mathematical analysis, they calculate the volume and surface area, leading to a paradoxical yet intriguing result. The video concludes with a teaser for a second question to be addressed in a follow-up video, encouraging viewers to stay tuned. The collaboration not only provides an entertaining look into advanced mathematics but also showcases the value of clear explanations and thought processes in problem-solving.
Takeaways
- 🎓 Steve from the channel 'Black Pen Red Pen' was introduced as a special guest on another channel, where he discusses his content focused on calculus and random topics.
- 📚 The host, an Oxford professor, interviews Steve using real Oxford interview questions, although it's not an actual admissions interview.
- 📈 They explore Gabriel's Horn, a mathematical problem involving the volume and surface area of a shape created by revolving the function 1/x around the x-axis.
- 🔢 Steve explains the formula for the volume of revolution, which involves integrating πy^2 dx from 1 to some large number 'a', and then taking the limit as 'a' approaches infinity.
- 🧮 The calculated volume of Gabriel's Horn is found to be π cubic units, which is a finite value.
- 📐 Steve and the host then discuss the surface area of revolution, which is more complex due to the slanted shape of Gabriel's Horn.
- 🚫 Upon attempting to calculate the surface area, they determine that it diverges to infinity, meaning it could never be completely covered or painted.
- 🤔 This leads to a paradoxical situation where a finite volume has an infinite surface area, highlighting the intriguing properties of calculus and geometry.
- 📉 The host and Steve use comparison tests to demonstrate why the surface area integral diverges, showcasing Steve's mathematical understanding.
- 👍 Steve's performance is praised, and the host encourages viewers to check out Steve's channel for more calculus content.
- 🔄 They hint at a second question to be explored in a subsequent video, keeping the audience engaged and looking forward to more content.
Q & A
Who is the special guest featured in the video?
-The special guest featured in the video is Steve from the channel 'black pen red pen'.
What type of content does Steve's channel focus on?
-Steve's channel focuses on calculus videos, with topics that are described as pretty random but enjoyable.
What is the educational background of the host of the channel?
-The host of the channel is an Oxford professor who conducts interviews and asks questions to candidates every year.
What is the first problem discussed in the interview?
-The first problem discussed in the interview is Gabriel's horn, which involves creating a volume of revolution from the function 1/X.
How is the volume of a revolution calculated?
-The volume of a revolution is calculated by integrating the area of a disk (pi * (radius)^2 * thickness) over the interval of interest, where the thickness is dx and the radius is the function value at that point.
What is the volume of Gabriel's horn?
-The volume of Gabriel's horn is found to be pi cubic units, which is a finite value.
What is the formula for the surface area of a revolution?
-The formula for the surface area of a revolution involves integrating the circumference (2 * pi * radius) times the differential length (dl), where dl is derived from the Pythagorean theorem considering the differential changes in x and y.
What is the surface area of Gabriel's horn?
-The surface area of Gabriel's horn is found to be infinite, which is a divergent integral.
What is the paradox presented by Gabriel's horn?
-The paradox presented by Gabriel's horn is that it has a finite volume but an infinite surface area, meaning it can be filled with a finite amount of paint but would take an infinite amount of time to paint the entire surface.
What is the purpose of the interview with Steve?
-The purpose of the interview with Steve is to have fun and explore interesting mathematical concepts, specifically by answering real Oxford interview questions related to calculus and integrals.
What is the nature of the second question that will be discussed in the next video?
-The nature of the second question is not specified in the script, but it is implied that it will be another challenging mathematical problem to be tackled in the next video.
Outlines
🎓 Introduction and Interview Setup
The video begins with the host welcoming Steve from the 'Black Pen Red Pen' channel as a special guest. Steve introduces himself and his channel, which focuses on calculus and random topics that he enjoys. The host, an Oxford professor, proposes an interview with Steve using real Oxford interview questions, although it's emphasized that this is not a genuine admissions interview. The first problem they tackle is Gabriel's horn, a mathematical problem involving calculus.
📚 Calculating Volume of Revolution
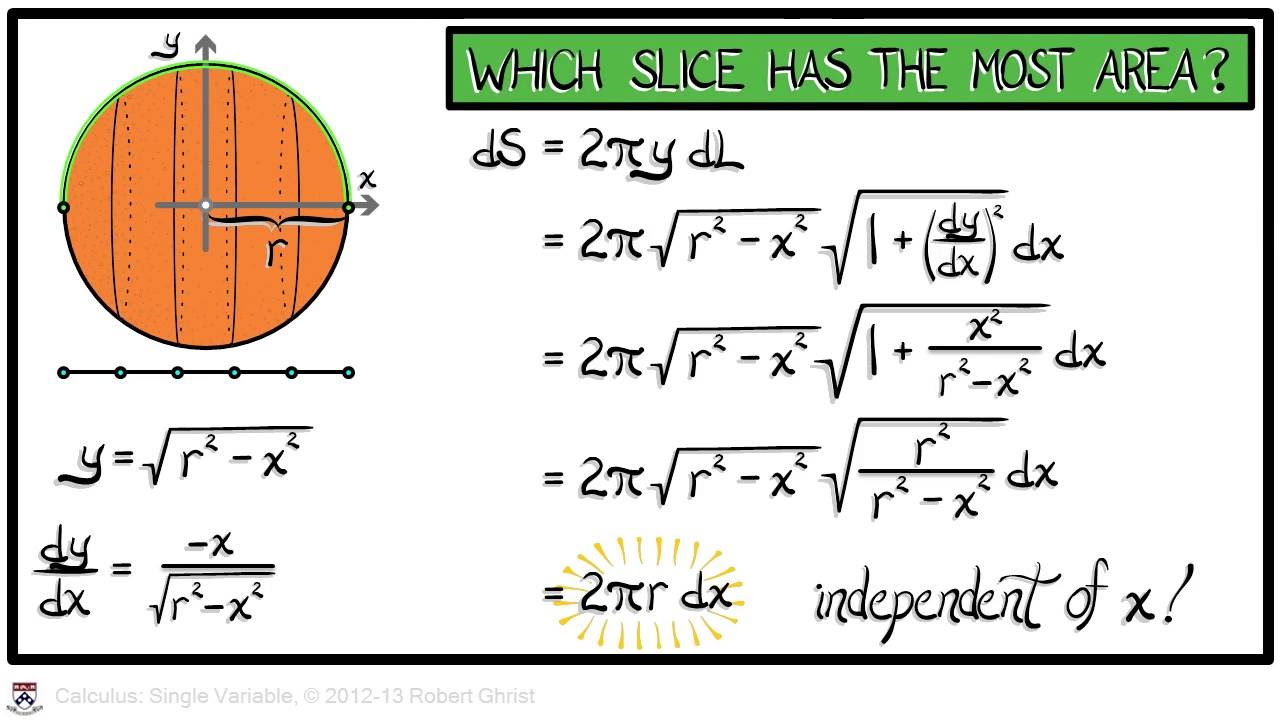
The discussion moves on to calculating the volume of revolution for the function 1/X by rotating it around the x-axis, creating Gabriel's horn. The formula for the volume of a disk is introduced, and it's explained how to integrate this formula over the function's domain to find the total volume. The limits for the integration are discussed, and the process involves taking the limit as it approaches infinity. The final calculation reveals that the volume of Gabriel's horn is π cubic units, despite its infinite height.
🔍 Surface Area of Gabriel's Horn
Following the volume calculation, the conversation shifts to finding the surface area of Gabriel's horn. Unlike the volume, the surface area cannot be calculated using the formula for a cylinder due to the horn's slanted shape. The correct approach involves integrating the circumference of the horn's cross-section over its length. The formula for the surface area involves the derivative of the function 1/X and the Pythagorean theorem. The integration process is outlined, and it's suggested that the surface area might be infinite, contrasting with the finite volume calculated earlier.
🤔 Gabriel's Horn Paradox and Conclusion
The paradox of Gabriel's horn is highlighted: despite having a finite volume that could theoretically be filled, the infinite surface area implies it could never be completely painted. This leads to a discussion on convergent and divergent integrals. The host commends Steve's performance and teases a second question to be addressed in a follow-up video. The video concludes with a recommendation for viewers to check out Steve's channel and a prompt to subscribe for more content.
Mindmap
Keywords
💡Calculus
💡Gabriel's Horn
💡Volume of Revolution
💡Surface Area of Revolution
💡Integral
💡Derivative
💡Oxbridge Interview Questions
💡Paradox
💡Black Pen Red Pen
💡Convergence and Divergence
💡Thought Process
Highlights
Introduction of Steve from the channel 'black pen red pen' who creates calculus videos.
Steve's channel features random topics with a focus on calculus, aiming to make the subject interesting.
The host, an Oxford professor, interviews Steve using real Oxford interview questions.
Steve willingly participates in a mock interview to answer challenging math questions.
Discussion of Gabriel's horn, a mathematical problem involving the volume of revolution.
Explanation of how to graph the function 1/x and compare it with 1/x^2.
Steve demonstrates the process of creating a volume of revolution by rotating 1/x around the x-axis.
Calculation of the volume of Gabriel's horn using the formula for the volume of a disk.
Steve explains the integral process to find the volume between 1 and a large number a.
Taking the limit as a approaches infinity to find the volume of the infinite horn.
Steve correctly calculates the volume of Gabriel's horn to be π.
Introduction of the surface area of revolution formula and its application to Gabriel's horn.
Steve works through the formula for the surface area, considering the slanted shape of Gabriel's horn.
Calculation of the surface area of Gabriel's horn and the realization that it diverges to infinity.
Steve concludes that Gabriel's horn has a finite volume but an infinite surface area, highlighting a mathematical paradox.
The host praises Steve's performance in the mock interview and encourages viewers to check out his channel.
A teaser for the second part of the interview with another challenging question to be featured in a follow-up video.
Transcripts
Browse More Related Video

Prime Reciprocal Series with @blackpenredpen (Oxford Maths Interview Question)

Gabriel's Horn Paradox - Numberphile

Oxford University Mathematician takes Admissions Interview (with @AnotherRoof)
Calculus Chapter 4 Lecture 36 Surface Area

2021 Live Review 7 | AP Calculus AB | Application of Integrals (Part 2)
Organic Chemistry Tutor - Youtube Channel Membership
5.0 / 5 (0 votes)
Thanks for rating: