Integration Technique - The Plus 1, Minus 1 Trick
TLDRThe video introduces a mathematical technique known as the +1 -1 trick, which simplifies the process of integration by avoiding long division. The trick involves adding and subtracting the same number to the numerator of a fraction, which changes its appearance without altering its value. This allows for easier integration by breaking down the integral into simpler parts that can be solved more directly. The video demonstrates this technique with several examples, such as integrating x over (x + 1), x + 4 over (x + 6), and x^3 over (x - 4). The method often results in natural logarithm terms and is presented as a quicker alternative to traditional substitution or long division, especially useful for solving multiple problems efficiently.
Takeaways
- 📚 The +1 -1 trick is a mathematical technique that allows for simplification of integrals without changing their value.
- ➕ By adding and subtracting the same number (e.g., 1), one can manipulate the integral to avoid long division.
- 🔍 This technique is particularly useful when the numerator is close to the denominator, making it easier to integrate.
- 🚀 It speeds up problem-solving by simplifying the process and often results in a natural logarithm term in the solution.
- 🌟 The trick can be adapted for different numbers, not just +1 and -1, but any pair that adds up to zero.
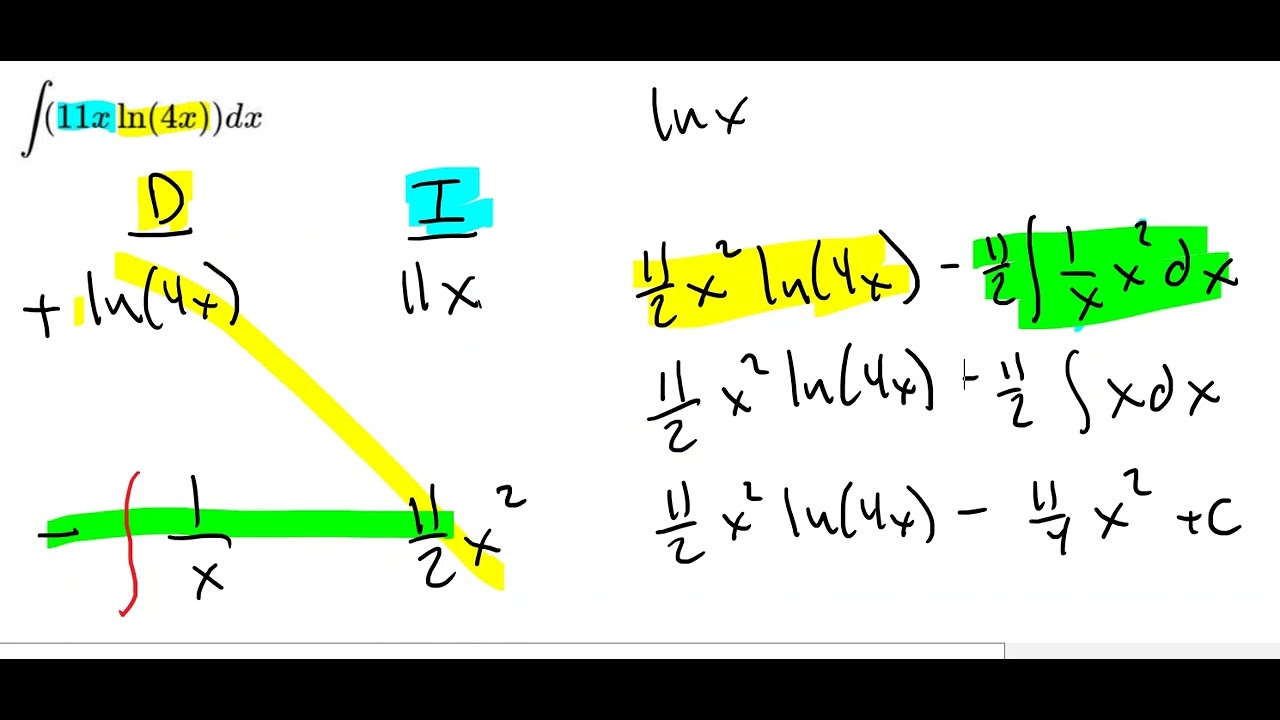
- ✅ An example given is integrating x over (x + 1) dx, which is simplified by adding and subtracting 1 in the numerator.
- 📉 The technique can be applied to more complex integrals, such as those involving polynomials and difference of cubes.
- 📌 Factoring is a key part of the process, especially when dealing with cubic terms or difference of cubes.
- 📐 The power rule is used to integrate polynomial terms after they have been separated from the more complex parts of the integral.
- ⏩ The method is faster than traditional long division and can be quicker than u-substitution for some problems.
- 🤓 Practicing the +1 -1 trick can improve one's comfort level and speed in solving complex integrals.
- 🎓 This technique is a valuable addition to a student's or mathematician's toolkit for solving integrals efficiently.
Q & A
What is the +1 -1 trick or technique mentioned in the video?
-The +1 -1 trick is a mathematical technique where you add and subtract the same number to the numerator of a fraction, which doesn't change the value but can simplify the expression and avoid long division.
How does the +1 -1 trick help in solving integrals?
-The trick allows you to create a term in the numerator that cancels out with the denominator, simplifying the integral and often resulting in a natural logarithm term, which is easier to integrate.
What is the first example given in the video to demonstrate the +1 -1 trick?
-The first example is the integral of x over (x + 1) dx. By adding and subtracting 1 in the numerator, the integral is broken into two parts, one of which simplifies to 1 dx, and the other remains as (1/(x + 1)) dx.
How is the +1 -1 trick applied to the integral of x + 4 over (x + 6) dx?
-The trick is applied by adding and subtracting 2 in the numerator to make it (x + 6), which then cancels out with the denominator, leaving you with two simpler integrals to solve.
What is the general form of the difference of cubes factorization?
-The difference of cubes factorization is given by a^3 - b^3 = (a - b)(a^2 + ab + b^2).
In the video, how is the integral of x^3 over (x - 4) dx approached using the +1 -1 trick?
-The integral is rewritten as (x^3 - 64 + 64) over (x - 4) dx. The x^3 - 64 factors into (x - 4)(x^2 + 4x + 16), and the +64 term is separated to be integrated on its own, simplifying the process.
What is the advantage of using the +1 -1 trick over other techniques like u-substitution?
-The +1 -1 trick can be faster than u-substitution in certain cases, especially when the numerator and denominator have similar terms that can be easily manipulated to cancel each other out.
What is the final result of the integral of x^3 over (x - 4) dx after applying the +1 -1 trick?
-The final result is (1/3)x^3 + 2x^2 + 16x + 64 * natural log |x - 4| + C.
Why is the absolute value used in the result of the integrals?
-The absolute value is used to ensure the result of the natural logarithm is defined, as the natural logarithm requires a positive argument.
Can the +1 -1 trick be applied to any integral?
-The +1 -1 trick is not universally applicable to every integral. It is particularly useful when the numerator and denominator have terms that can be made to cancel out by adding and subtracting the same value.
What is the purpose of the constant C in the final answer of an integral?
-The constant C represents the constant of integration, which accounts for an arbitrary constant that may be present in the antiderivative of the function.
Outlines
🔢 The +1 -1 Trick for Simplifying Integration
This paragraph introduces a mathematical technique known as the +1 -1 trick, which is a method to simplify the process of integration without resorting to long division. The trick is based on the principle that adding and subtracting the same number (in this case, 1) does not change the value of an expression. The speaker demonstrates how this technique can be applied to integrals such as ∫x/(x+1)dx by adding and subtracting 1 in the numerator, effectively transforming the integral into a more manageable form. The process is further illustrated with additional examples, including integrals with different numerators and denominators, showcasing how the trick can simplify complex-looking integrals into a combination of natural logarithms and polynomials.
🚀 Faster Integration with the +1 -1 Trick
The second paragraph emphasizes the efficiency of the +1 -1 trick in comparison to other methods like long division or u-substitution. The speaker suggests that while these other techniques can yield the correct answer, the +1 -1 trick can often be faster and is particularly useful when solving multiple problems quickly. The paragraph concludes with an encouragement for the viewer to try out the technique and wishing them good luck, highlighting the presenter's aim to provide helpful and practical advice for mathematical problem-solving.
Mindmap
Keywords
💡+1 -1 trick
💡Long division
💡Integral
💡Numerator
💡Denominator
💡Substitution
💡Natural log
💡Factor
💡Polynomial
💡U substitution
Highlights
The +1 -1 trick, also called a technique, is introduced as a method to simplify calculations.
The core concept is that adding and subtracting 1 (or any number) doesn't change the value of an expression, allowing for easier manipulation.
This trick helps to avoid long division, making calculations quicker and more efficient.
The first example demonstrates integrating x over (X plus 1) dx by manipulating the numerator to match the denominator.
The integral is broken down into two parts, simplifying the process and often resulting in a natural logarithm.
The technique can be applied with different numbers, not just +1 -1, as shown in the second example with x plus 4 over x plus 6.
By adding and subtracting the same term, the expression's appearance changes without altering its value, facilitating integration.
The third example involves a more complex integral, x cubed over (X minus 4) dx, which is simplified by factoring and applying the trick.
The difference of cubes formula is used to factor x cubed minus 64, making the integral easier to solve.
The integral is further simplified by separating it into two parts, one of which can be integrated immediately.
The final result of the integral includes terms like X cubed, 2x squared, 16x, and a natural logarithm, showcasing the power of the trick.
Long division is avoided throughout the process, which can be time-consuming; instead, the +1 -1 trick offers a faster alternative.
U-substitution is mentioned as another technique that could be used, but the +1 -1 trick is preferred for its speed.
The presenter emphasizes the trick's utility in quickly solving a variety of integral problems.
The method is applicable to a wide range of integral problems, offering a versatile approach to calculus.
The video concludes with a reminder that while the +1 -1 trick is helpful, it's also important to understand the underlying concepts.
Good luck is wished to the viewers, encouraging them to apply the +1 -1 trick to their calculus problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: