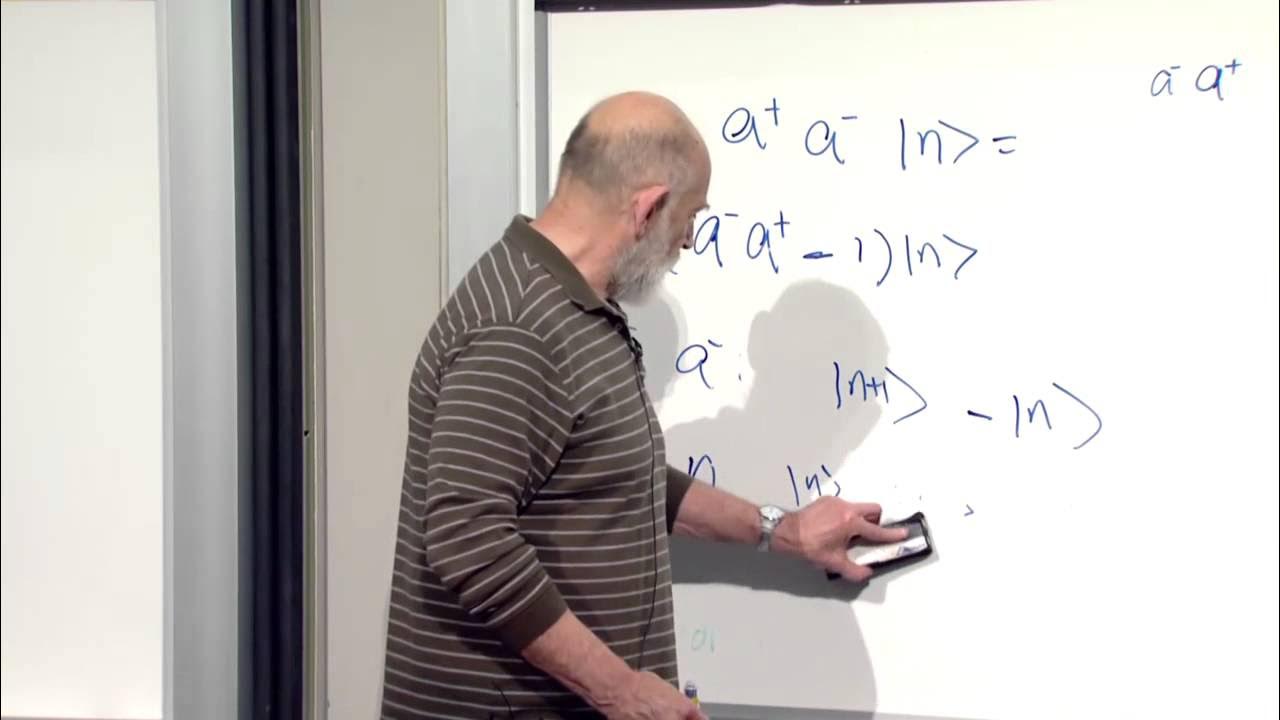Advanced Quantum Mechanics Lecture 8
TLDRThe transcript appears to be a lecture on quantum mechanics, focusing on the behavior of neutrinos, the concept of particle spin, and the principles of second quantization. The lecturer discusses the mixing of neutrino states, their oscillation, and the implications for energy conservation. They delve into the mathematics of quantum tunneling and the superposition of states, using the example of a particle in a potential well to illustrate these concepts. The lecture also touches on the measurement of electric dipole moments, the violation of symmetries like reflection and time-reversal symmetry in particle physics, and the standard model's predictions. The lecturer emphasizes the importance of these principles in understanding the quantum mechanical behavior of particles and fields, hinting at the upcoming discussion on fermions and their role in quantum field theory.
Takeaways
- 🚀 The concept of neutrino oscillation is introduced, explaining how neutrinos can change from one type to another as they propagate through space.
- 🌌 Neutrinos have different masses, and this mass difference is crucial for the phenomenon of neutrino oscillation, which is not possible if neutrinos are massless.
- ⚛️ The potential barrier in quantum mechanics is used as an analogy to explain the mixing of neutrino states, similar to how particles in a double-well potential can mix states.
- 📈 The energy levels of neutrinos are initially very small, but the mixing between them causes a slight splitting in energy levels, which is experimentally observable.
- 🔬 The experiment involving electron neutrinos and muon neutrinos demonstrates that neutrinos can oscillate between different 'flavors', which has implications for our understanding of particle physics.
- 🤔 The question of why neutrinos have mass and what determines the size of the mass difference (ε) is linked to the parameters of the neutrino potential, which is still a topic of research.
- 🧲 The electron is not a sphere, and its charge distribution can be described by higher-order multipole moments. The absence of an electric dipole moment in the electron is not evidence of its sphericity.
- 🔋 The electric dipole moment (EDM) of the electron is a measure of charge imbalance and is related to the violation of certain fundamental symmetries, which is forbidden in the standard model of particle physics.
- ⏳ Time reversal symmetry, if it were an exact symmetry of nature, would imply that the electron cannot have an EDM. However, small violations of this symmetry are observed and can lead to a very small EDM.
- 🔬 The experimental search for the electron's EDM is an effort to test the standard model of particle physics and to look for new physics beyond the standard model.
- ✨ The script touches on the mathematical foundations of quantum field theory, including the use of Fourier transforms and the relationship between wave functions in position and momentum space.
Q & A
What is the phenomenon of neutrino mixing?
-Neutrino mixing is a quantum mechanical process where neutrinos can oscillate between different flavors (electron, muon, and tau) as they propagate through space. This phenomenon occurs because neutrinos have mass and their flavor states are not the same as their mass states.
Why is the mass of neutrinos significant in particle physics?
-The mass of neutrinos is significant because it implies that the laws of physics distinguish between left-handed and right-handed particles, breaking the symmetry known as reflection symmetry. This has profound implications for our understanding of the universe and the standard model of particle physics.
What is the connection between the mass of neutrinos and energy conservation?
-The mass of neutrinos is related to energy conservation through the principle of mass-energy equivalence (E=mc^2). The mixing of neutrino states with different masses leads to a small splitting in their energy levels, which is consistent with energy conservation in quantum mechanics.
How does the potential in a quantum system affect the energy levels and wave functions of a particle?
-The potential in a quantum system determines the energy levels and shapes of the wave functions. If the potential is symmetric, the energy eigenstates are either symmetric or anti-symmetric. The wave functions of a particle in such a system can be a linear combination of these eigenstates, leading to phenomena like quantum tunneling and energy level splitting.
What is the significance of the electron not having an electric dipole moment according to the standard model?
-The absence of an electric dipole moment in an electron is consistent with the symmetries of the standard model, which predicts that such a moment should be extremely small or non-existent. The experimental non-detection of an electron's electric dipole moment places constraints on possible extensions to the standard model and makes it more challenging to introduce new physics that could explain phenomena like dark matter or the matter-antimatter asymmetry.
What does the term 'second quantization' refer to in quantum mechanics?
-Second quantization is a formalism in quantum mechanics that allows for the treatment of systems with a variable number of particles. It introduces creation and annihilation operators to describe the addition and removal of particles in a quantum state, which is particularly useful for systems like quantum fields that can have particles created or destroyed.
How does the Heisenberg Uncertainty Principle relate to the non-commutativity of certain operators?
-The Heisenberg Uncertainty Principle states that there is a limit to the precision with which certain pairs of physical properties, like position and momentum, can be known simultaneously. This is related to the non-commutativity of the corresponding operators in quantum mechanics. When two operators do not commute, it means that the physical quantities they represent cannot be precisely measured at the same time, reflecting the uncertainty principle.
What is the role of the Hamiltonian in determining energy eigenstates in quantum mechanics?
-The Hamiltonian operator, representing the total energy of a system, is crucial in quantum mechanics for determining the energy eigenstates. The eigenstates of the Hamiltonian are the states for which the energy is definite, and the corresponding eigenvalues give the energy levels of the system. For a free particle, the energy eigenstates are typically described by momentum, not by position.
Why is the concept of spherical symmetry ambiguous when applied to quantum mechanical systems?
-In quantum mechanics, spherical symmetry is ambiguous because quantum systems can exhibit a superposition of states. A system may appear lopsided in a snapshot, but due to the wave function being rotationally symmetric, the probability distribution over time is spherically symmetric. The concept of spherical symmetry in quantum mechanics is therefore dependent on the time scale and the type of measurement performed.
What is the difference between a fermion and a boson in terms of their creation and annihilation operators?
-Fermions and bosons are two types of particles with different quantum mechanical properties. Fermions obey the Pauli exclusion principle and their creation and annihilation operators anti-commute, meaning that no two fermions can occupy the same quantum state simultaneously. Bosons, on the other hand, can occupy the same state and their operators commute. This difference leads to different statistical behaviors and is reflected in the commutation relations of their respective field operators.
How does the concept of 'tunneling' relate to the potential barrier in a quantum system?
-Tunneling is a quantum mechanical phenomenon where a particle can pass through a potential barrier even if its energy is less than the barrier height. This occurs due to the wave-like nature of particles in quantum mechanics, allowing them to exist in a superposition of states and penetrate classically forbidden regions. The probability of tunneling depends on the size of the barrier and the energy of the particle.
Outlines
😀 Neutrinos and Quantum Mechanics
The paragraph delves into particle physics, discussing neutrinos and their properties. It highlights that neutrinos do not all have the same mass and introduces the concept of neutrino mixing. The speaker uses the analogy of a particle in a potential well to explain the phenomenon of mixing in quantum mechanics, touching on the ideas of energy eigenstates, symmetric and anti-symmetric wave functions, and the implications of a symmetric potential on these states.
🧐 Quantum Superposition and Energy States
This section explores the concept of superposition in quantum mechanics. It describes how energy eigenstates can be linear combinations of other states, using the example of a particle in a double-well potential. The speaker explains how the ground state and excited states of the system can be expressed as symmetric and anti-symmetric combinations of wave functions, and how these states evolve over time, leading to a phenomenon known as quantum tunneling.
🌀 Time Evolution of Quantum States
The paragraph discusses the time dependence of quantum states. It describes how, starting with a particle in a specific state, the system evolves over time due to the different phases of the energy eigenstates. The speaker illustrates how the particle's state can transition from one side of the potential barrier to the other, explaining the process of oscillation between states and how this is represented mathematically in the Schrödinger equation.
🤔 The Phenomenon of Neutrino Oscillation
This part of the script focuses on the behavior of neutrinos, drawing parallels between the quantum mechanical concepts discussed and the observed behavior of neutrinos. It explains how neutrinos created in certain types of decays can oscillate between different types, such as electron neutrinos transforming into muon neutrinos. The speaker also touches on the experimental verification of neutrino oscillation and the sensitivity of this phenomenon to various parameters.
🔬 The Standard Model and Neutrino Mass
The speaker reflects on the implications of neutrino oscillation for our understanding of the standard model of particle physics. They note that the existence of neutrino mass is not accommodated within the standard model, suggesting that the observation of neutrino oscillation implies a violation or extension of the current theoretical framework. The paragraph also mentions the experimental fact of neutrino oscillation and its significance in particle physics.
🤓 Quantum Tunneling and Particle Behavior
The paragraph discusses the concept of quantum tunneling, using the example of a particle moving through a barrier that it classically shouldn't be able to surmount. It explains how the mathematics of this process is analogous to other quantum phenomena, such as the behavior of spins in a magnetic field. The speaker also addresses a question about the representation of a nitrogen molecule and its tunneling behavior.
📡 Spin States and Magnetic Fields
This section explores the relationship between spin states and magnetic fields. It describes how the application of a magnetic field can alter the energy of spin states, leading to phenomena such as spin precession. The speaker discusses how the orientation of a particle's spin can affect its energy in a magnetic field, and how this can lead to oscillations between spin states, drawing parallels with the behavior of neutrinos.
🔍 The Search for the Electron's Electric Dipole Moment
The speaker discusses the concept of an electric dipole moment (EDM) and its implications for the understanding of fundamental particles like the electron. They explain that the absence of an EDM for the electron is not evidence of its spherical nature, but rather an indication of certain symmetries in physics. The paragraph also touches on the experimental efforts to detect an EDM, which could challenge the standard model of particle physics.
🧲 Magnetic Moments and Particle Spin
This part of the script focuses on the magnetic properties of particles, particularly electrons. It explains that electrons have a magnetic moment due to their spin, which is often visualized as a current loop. The speaker clarifies that this magnetic property does not imply a spherical charge distribution, as the electron's spin introduces an axis of rotation, which is inherently non-spherical.
🚀 Second Quantization and Field Theory
The speaker introduces second quantization, a method used in quantum mechanics to describe systems of identical particles. They explain the connection between wave functions and field operators, and how creation and annihilation operators are used to represent particles with different momenta. The paragraph outlines the mathematical framework of second quantization and its relevance to quantum field theory.
🤨 Commutators and Quantum Measurements
The paragraph discusses the commutators of quantum mechanics, which are integral to understanding the uncertainty principle. The speaker explains how the commutator of position and momentum operators leads to the uncertainty in simultaneous measurements of these quantities. They also touch on the concept of locality and how the commutation relations of field operators at different points reflect the independence of measurements at those points.
🚨 Fermions and Bosons in Quantum Field Theory
The speaker concludes with a brief mention of fermions and bosons, two types of particles that are described by different types of field operators in quantum field theory. They note that fermions, such as electrons, follow the Pauli exclusion principle and anti-commute, while bosons, such as photons, commute. This distinction has profound implications for the behavior of these particles and their interactions.
Mindmap
Keywords
💡Neutrino
💡Quantum Mechanics
💡Energy Conservation
💡Particle Oscillation
💡Schrodinger Equation
💡Tunneling
💡Magnetic Field
💡Electric Dipole Moment
💡Symmetry Breaking
💡Standard Model
💡Second Quantization
Highlights
Evidence suggests that neutrinos have mass and they mix, a phenomenon not addressed in particle physics classes.
Neutrinos do not all have the same mass, leading to questions about energy conservation in their mixing.
The mass of neutrinos is related to energy, with mass states being linear superpositions of other states, leading to quantum mechanical phenomena like mixing.
A potential well example illustrates the concept of particle tunneling and the quantum mechanical phenomenon of energy level mixing.
The ground state wave function and energy of a system can be determined by considering the symmetry of the potential and the theorems of quantum mechanics.
The phenomenon of neutrino oscillation is analogous to the quantum mechanical mixing of states, with neutrinos changing their type over time.
Neutrino oscillation experiments have shown that neutrinos can transform from one type to another, challenging the initial understanding of their properties.
The size of the energy difference (Epsilon) in neutrino oscillations is determined by various factors, including the mass of the neutrino and the characteristics of the potential barrier.
The concept of neutrino mass introduces a small parameter in the standard model of particle physics, which is not well understood and suggests a violation of the model.
The experiment on the electron's electric dipole moment (EDM) provides insights into the symmetry of the electron's charge distribution and its quantum mechanical properties.
The electron is not spherically symmetric due to its spin, which introduces an axis and a magnetic moment, contradicting the idea that it could be a perfect sphere.
The search for an electron's EDM is connected to fundamental symmetries like reflection and time reversal symmetry, which are not exact in the physical world.
The non-existence of an electron's EDM is a result consistent with the standard model of particle physics, making it challenging to introduce modifications to the model.
The mathematical framework of second quantization allows for the connection between wave functions in position and momentum space with creation and annihilation operators.
In second quantization, the field operators for different positions and momenta are related through Fourier transforms, similar to how wave functions are in quantum mechanics.
The commutation relations of field operators at different points in space imply that measurements at one point do not interfere with measurements at another, upholding the principle of locality.
The concept of entanglement in quantum mechanics does not violate the principle of no faster-than-light influence because measurements at different points commute.
Fermion fields, unlike boson operators, anti-commute at different points, implying a fundamentally different behavior that challenges the notion of independent measurements.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: