17. Ray or Geometrical Optics II
TLDRThe video script is a detailed lecture on geometrical optics, delivered by a professor to his class. It begins with a scenario of explaining geometrical optics in an elevator pitch, emphasizing the Principle of Least Time as a fundamental concept that encompasses various phenomena such as reflection, Snell's law, and focusing of light. The professor delves into the specifics of light behavior when interacting with mirrors and lenses, including the formation of images and the mathematics behind the focal points. The discussion covers the use of parabolic and spherical mirrors, the limitations of approximations, and the impact of object size on image quality. The lecture also touches on the human eye, its ability to adapt and focus, and the concept of magnification using lenses. The professor concludes with a teaser for the next lecture, hinting at the need for new theories to address contradictions found in experiments.
Takeaways
- 📈 The Principle of Least Time is fundamental in geometrical optics, explaining phenomena like reflection and refraction.
- 🔄 Snell's Law and the law of reflection can be derived from the Principle of Least Time.
- 🗺️ A parabolic mirror can focus parallel rays of light to a single point because all paths satisfy the Principle of Least Time.
- 📐 The equation of a parabola, which describes the shape of the mirror for optimal focusing, is y^2 = 4xf, where f is the focal length.
- 🕵️♂️ Focusing light rays to a single point is only possible when considering rays that take the same amount of time to travel from the source to the mirror and back.
- 🌐 A spherical mirror is an approximation of a parabolic mirror, derived from a section of a sphere, and is useful for focusing parallel light rays close to the axis.
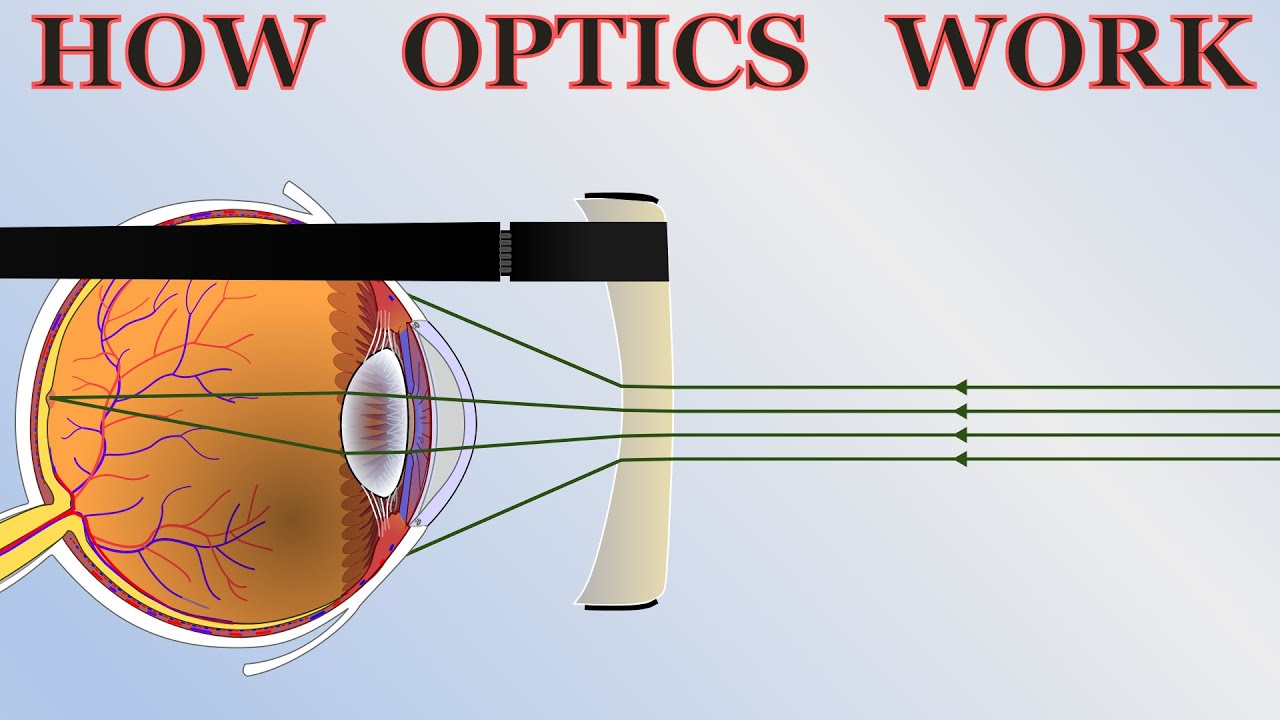
- 🔍 The human eye can adjust the focal length by changing the shape of the lens, a process known as accommodation, to focus on objects at various distances.
- 👓 The near point of the human eye, the closest distance at which it can focus, is approximately 25 centimeters.
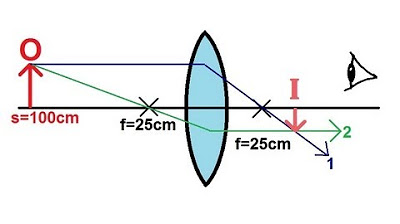
- 🔬 Magnifying glasses and microscopes work by creating virtual images that appear to be at a greater distance than the near point, thus magnifying the viewable angle.
- 📐 The magnification power of a lens is determined by the lens formula 1/f = 1/u + 1/v, where f is the focal length, u is the object distance, and v is the image distance.
- 🤔 The limitations of geometrical optics, such as the inability to focus on objects closer than the near point without additional optical devices, highlight the need for more advanced models to explain certain optical phenomena.
Q & A
What is the Principle of Least Time in the context of geometrical optics?
-The Principle of Least Time, also known as Fermat's Principle, states that the path taken by light between two points is the path that takes the least time. This principle is used to derive several laws in optics, such as the law of reflection and Snell's law of refraction.
How does the Principle of Least Time explain the law of reflection?
-According to the Principle of Least Time, for light to take the least amount of time in its journey, the angle of incidence must equal the angle of reflection. This is because any other path would take more time, thus violating the principle.
What is Snell's law and how does it relate to the Principle of Least Time?
-Snell's law describes the relationship between the angles of incidence and refraction when light passes through a medium with a different refractive index. It is derived from the Principle of Least Time, as the light path that satisfies Snell's law is the one that minimizes the travel time.
What is a parabolic mirror and how does it relate to the focusing of light?
-A parabolic mirror is a type of mirror that has the shape of a parabola. It is used to focus parallel rays of light to a single point, known as the focus of the parabola. This property is derived from the Principle of Least Time, as all rays reflecting off the parabola take the same amount of time to reach the focus.
How does a spherical mirror approximate a parabolic mirror?
-A spherical mirror can approximate a parabolic mirror by taking a section of a sphere and using it as a mirror. The focal length of the spherical mirror is approximately equal to half the radius of the sphere (R/2). However, this is only a good approximation for rays close to the mirror's axis.
What is the significance of the focal point in the context of mirrors and lenses?
-The focal point is the point where parallel rays of light converge after reflecting off a mirror or passing through a lens. In the context of mirrors, it is the point behind the mirror where the reflected rays of a distant object appear to originate. In lenses, it is the point where parallel rays of light meet after passing through the lens.
What is the difference between a real image and a virtual image?
-A real image is formed when light rays actually converge at a point and can be projected onto a screen. A virtual image, on the other hand, is formed when light rays appear to diverge from a point but do not actually meet. A virtual image cannot be projected onto a screen but can be observed directly.
How does the human eye adjust its focal length to focus on objects at different distances?
-The human eye can adjust its focal length through a process called accommodation. The lens of the eye is made of a flexible material and is attached to muscles. By contracting or relaxing these muscles, the shape and thus the focal length of the lens can be changed, allowing the eye to focus on objects at varying distances.
What is the near point of the human eye and why is it significant?
-The near point of the human eye is the closest distance at which the eye can focus clearly. It is typically about 25 centimeters away from the eye. This limit is significant because it determines the closest point at which an object can be seen in sharp focus without the eye's muscles becoming fatigued.
How does a magnifying glass or microscope work and what is the principle behind it?
-A magnifying glass or microscope works by placing an object closer to the eye than the near point can allow, thus creating a virtual image that appears larger. The principle behind it is that by adjusting the focal length of the lens and the position of the object (u), the angle of the light rays (θ) that reach the eye is increased, making the object appear magnified.
What is the significance of the refractive index in optics and how does it affect the path of light through a lens?
-The refractive index (n) of a material is a measure of how much light slows down in that material as compared to a vacuum. When light passes through a lens, the refractive index affects the path of light by bending it more or less depending on the difference in refractive indices between the lens material and the surrounding medium. This bending of light, or refraction, is crucial for the focusing of light by the lens.
Outlines
😀 Introduction to Geometrical Optics and the Principle of Least Time
The professor begins by emphasizing the importance of understanding optics, suggesting that the interlude will allow students to catch up and stay ahead. An elevator presentation of geometrical optics is discussed, where the Principle of Least Time is highlighted as a fundamental concept that encompasses various phenomena such as the law of reflection and Snell's law. The presentation also touches on the special case of focusing light rays and how multiple paths can satisfy the principle, leading to the concept of a focal point.
🔍 Geometrical Optics: Mirrors and the Formation of Images
The discussion shifts to the use of mirrors in geometrical optics, particularly for forming images of objects at finite distances. The professor addresses the need for clear communication with the class regarding any difficulties in reading the board. The principles of ray optics learned in high school are reviewed, such as the behavior of parallel rays and those passing through the focal point. The consistency of these principles is demonstrated through the use of additional rays and the relationship between object distance (u), image distance (v), and the focal length (f).
📐 Calculations and Approximations in Ray Optics
The professor delves into the mathematical aspects of ray optics, focusing on the calculation of distances (d_1 and d_2) for rays reflecting off a parabolic mirror. The goal is to show that the total travel time for light rays is independent of the height (y) of their incidence on the mirror. It is emphasized that the calculation should not depend on y, and approximations are made to ensure this, highlighting the importance of understanding when to include or omit terms in an equation.
🌟 Limitations of Mirrors and the Concept of Focal Length
The limitations of using mirrors to form images are discussed, with the professor explaining that while a parabolic mirror can focus parallel light rays regardless of their width, it cannot form a perfect image if the object is too tall or not at infinity. The concept of focal length is also revisited, with an explanation of how it can be manipulated by changing the refractive index (n) or the radius of curvature (R) of the mirror.
🤓 Human Eye and Accommodation
The professor turns to the human eye, describing its remarkable ability to adjust focus despite the brain's inversion of the visual image. The eye's lens, made of a flexible material, can change shape to alter the focal length, allowing the eye to focus on objects at various distances. However, there is a limit to this accommodation, known as the near point, which is typically around 25 centimeters. The eye's ability to adapt and the concept of magnification using lenses are also briefly mentioned.
🔬 Magnification and the Role of Lenses
The use of magnifying lenses to improve the angle subtended by an object to the eye is explained. The professor discusses how the magnification achieved by a lens is dependent on the object's distance (u) and the lens's focal length (f). The importance of placing the object at the focal point to minimize eye strain and the concept of viewing objects at an effective 'infinity' are highlighted. The summary concludes with a teaser for the next lecture, where the professor promises to discuss reasons for changing the rules of geometrical optics based on contradicting experiments.
Mindmap
Keywords
💡Principle of Least Time
💡Snell's Law
💡Mirror
💡Parabolic Mirror
💡Spherical Mirror
💡Focal Length
💡Lenses
💡Virtual Image
💡Human Eye
💡Magnification
💡Near Point
Highlights
The Principle of Least Time is used to explain various phenomena in geometrical optics, including reflection and refraction.
Incident and reflected angles being equal can be derived from the Principle of Least Time.
Snell's Law is also a consequence of the Principle of Least Time, governing how light bends at an interface between two media.
Focusing of light is explained as a special case where multiple light rays take the same time to travel from a point to a common focal point.
A parabolic mirror can focus a parallel beam of light to a single point due to the property of having the same distance from the focal point and the reflective surface.
The equation of a parabola, y^2 = 4xf, is derived to show how it relates to the mirror's shape and the focal length.
Spherical mirrors are an approximation of parabolic mirrors and have a focal length related to the sphere's radius.
Limitations of using spherical mirrors for focusing are discussed, noting that they work well for small deviations from the axis.
The concept of image formation by mirrors for objects at finite distances is explored, highlighting the need to consider different ray paths.
The importance of accurate handwriting and font size for comprehension in a classroom setting is emphasized.
The use of approximations in calculations is discussed, stressing the importance of recognizing small parameters and their impact on results.
The relationship between the height of an object, the mirror, and the image is shown to be consistent with the Principle of Least Time.
The impact of the object's size on the quality of the image formed by a parabolic mirror is analyzed, noting that very large objects won't form a perfect image.
The human eye's ability to adjust the focal length through muscle control is highlighted, demonstrating the eye's remarkable accommodation mechanism.
The near point of the human eye, approximately 25 centimeters, is introduced as the closest distance the eye can focus on clearly.
The use of a magnifying lens to overcome the eye's accommodation limit and to see objects at a larger angle is explained.
The magnification provided by a lens is calculated based on the lens's focal length and the near point distance of the human eye.
The concept of forming a virtual image at infinity to reduce eye strain and allow the eye's muscles to relax is discussed.
The practical applications of geometrical optics, such as in the design of mirrors and lenses, are emphasized to motivate the study of optics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: