Molarity, Molality, Volume & Mass Percent, Mole Fraction & Density - Solution Concentration Problems

The Organic Chemistry Tutor

21 Jan 202131:25

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video delves into the concepts of solution concentration, explaining key terms such as mass percent, volume percent, mole fraction, molality, and molarity. It clarifies the roles of solute and solvent in a solution and provides formulas and examples for calculating concentration metrics. The video employs a step-by-step approach to tackle various chemistry problems, enhancing understanding of solution concentration calculations.

Takeaways

📚 The difference between solute and solvent is crucial: the solute is what dissolves, and the solvent does the dissolving.
🧪 Mass percent is calculated as (mass of solute / mass of solution) x 100%, which provides the concentration of the solute in the solution.
📊 Volume percent, denoted as v%, is similar to mass percent but uses volume instead of mass: (volume of solute / volume of solution) x 100%.
📏 Mole fraction is the ratio of moles of a particular substance to the total moles of all substances in the solution.
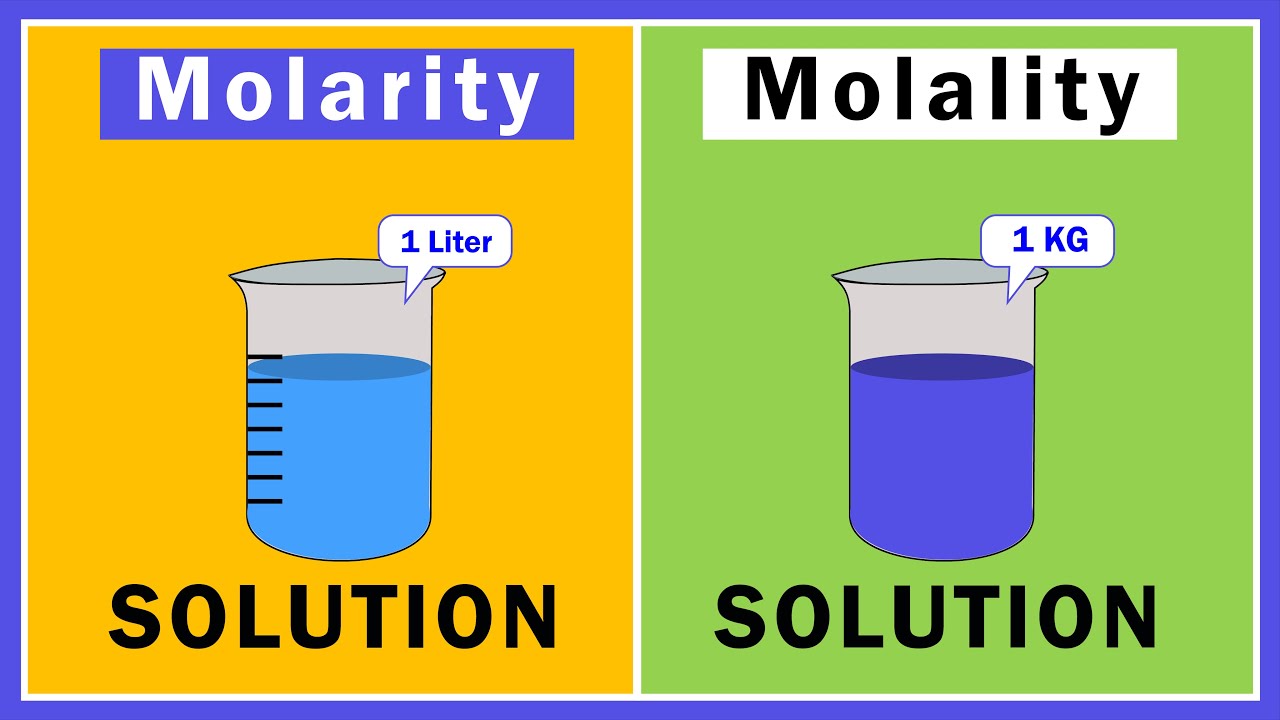
📉 Molarity (M) is the moles of solute per liter of solution, which is different from molality, which is moles of solute per kilogram of solvent.
🔍 Density is mass per unit volume and is commonly expressed in grams per milliliter (g/mL) or grams per cubic centimeter (g/cm³).
⚖️ To calculate mass percent, you need to know the mass of the solute and the total mass of the solution, which includes both solute and solvent.
🧪 For volume percent, you need the volume of the solute and the total volume of the solution, which is the sum of the volumes of solute and solvent.
🧬 Mole fraction is used to express the amount of a particular substance in a mixture relative to the total amount of all substances.
🧪 Molarity is a concentration measurement that requires the volume of the solution to be in liters, making it solution volume-dependent.
🧪 Molality, on the other hand, is independent of the solution volume and depends solely on the mass of the solvent.

Q & A

What is the difference between solute and solvent in a solution?
-The solute is the substance that is dissolved, while the solvent is the substance that does the dissolving. In the given example, sodium chloride is the solute and water is the solvent.
How is mass percent calculated in a solution?
-Mass percent is calculated as the mass of the solute divided by the mass of the solution, multiplied by 100 percent.
What is the formula for calculating volume percent?
-Volume percent is calculated as the volume of the solute divided by the volume of the solution, multiplied by 100.
How is mole fraction determined for a substance in a solution?
-The mole fraction of a substance is determined by dividing the moles of that substance by the total moles of all substances in the solution.
What is the difference between molarity and molality?
-Molarity is the moles of solute per liter of solution, while molality is the moles of solute per kilogram of solvent. They both involve moles of solute, but the denominator is different.
What is the formula for calculating molarity?
-Molarity is calculated as the moles of the solute divided by the liters of the solution.
How is the mass percent of sodium chloride in a solution calculated, given 15 grams of sodium chloride dissolved in 225 grams of water?
-The mass percent is calculated as (mass of solute / mass of solution) * 100%. So, it would be (15g / (15g + 225g)) * 100%, which equals 6.25%.
What is the volume percent of methanol when 25 milliliters of methanol is mixed with 150 milliliters of water?
-The volume percent is calculated as (volume of solute / volume of solution) * 100%. So, it would be (25 mL / (25 mL + 150 mL)) * 100%, which equals approximately 14%.
How is the mole fraction of potassium chloride (KCl) calculated when 2 moles of KCl are dissolved in 8 moles of water?
-The mole fraction of KCl is calculated as the moles of KCl divided by the total moles of all substances in the solution, which is (2 moles KCl) / (2 moles KCl + 8 moles H2O) = 2/10 = 0.2.
What is the molarity of a solution if 15 grams of sodium bromide (NaBr) is dissolved in 400 milliliters of solution?
-First, calculate the moles of NaBr using its molar mass (approximately 102.9 g/mol), then convert the volume of the solution from milliliters to liters (400 mL = 0.4 L), and finally divide the moles of NaBr by the liters of solution to find molarity.
How is the molality of a solution calculated when 10 grams of sodium hydroxide (NaOH) is dissolved in 500 grams of water?
-First, calculate the moles of NaOH using its molar mass (approximately 40 g/mol). Then convert the mass of the solvent (water) from grams to kilograms (500 g = 0.5 kg). Molality is then the moles of solute divided by the kilograms of solvent.
Given the mass percent and density of a solution, how can you calculate its molarity?
-Use the mass percent to find the mass of the solute in a known mass of solution (often 100 grams for simplicity). Convert this mass to moles using the solute's molar mass. Then, use the density to find the volume of the solution in liters. Finally, calculate molarity by dividing the moles of solute by the liters of solution.

Outlines

00:00

📚 Introduction to Solution Concentration

This paragraph introduces the topic of solution concentration, covering various measures such as mass percent, volume percent, mole fraction, molality, density, and molarity. It emphasizes the importance of understanding the concepts of solute and solvent, using sodium chloride in water as an example. The solute is the substance being dissolved (sodium chloride), while the solvent does the dissolving (water). The paragraph outlines formulas for mass percent, volume percent, and mole fraction, and distinguishes between molarity and molality, noting the key differences in their calculations.

05:02

🧪 Calculating Mass and Volume Percent

The second paragraph provides a step-by-step approach to calculating mass percent and volume percent in solutions. An example calculation is given for a solution containing 15 grams of sodium chloride dissolved in 225 grams of water to find the mass percent of sodium chloride. The process involves identifying the solute and solvent, calculating the total mass of the solution, and applying the mass percent formula. The paragraph also tackles a problem involving methanol and water, explaining how to determine the volume percent of methanol and the mass percent of water, with attention to how the wording of the question can influence which substance is treated as the solute.

10:02

📏 Density and Mole Fraction Calculations

This paragraph discusses the concept of density and its relevance to solution concentration problems. It explains the basic conversions between grams, kilograms, milliliters, and liters. The paragraph then proceeds to calculate the mole fraction of potassium chloride (KCl) in a solution where two moles of KCl are dissolved in eight moles of water. It also addresses the calculation of the mole fraction of sodium fluoride in a solution mixed with water, emphasizing the need to convert grams to moles using molar masses from the periodic table.

15:03

🧪 Molarity and Molality Calculations

The fourth paragraph delves into the calculation of molarity and molality. It outlines the process of finding the molarity of a solution with 15 grams of sodium bromide dissolved in 400 milliliters of solution. The calculation involves converting grams to moles using the molar mass of sodium bromide and then converting milliliters to liters to find the volume of the solution. The paragraph also explains how to calculate the molality of a solution with 10 grams of sodium hydroxide dissolved in 500 grams of water, highlighting the conversion from grams to kilograms for the solvent.

20:03

🔍 Advanced Solution Concentration Problems

The fifth paragraph presents a more complex problem involving the calculation of molarity from the mass percent and density of a solution. It walks through the process of finding the molarity of a solution with a 15% mass percent of aluminum chloride (AlCl3) and a density of 1.17 grams per milliliter. The solution involves using the mass percent to find the mass of aluminum chloride in 100 grams of solution, applying the density to find the volume of the solution in liters, and then calculating molarity using the molar mass of AlCl3.

25:04

🧠 Understanding Solute and Solvent Identification

The final paragraph clarifies the process of identifying solutes and solvents in various scenarios, especially when dealing with two possible solvents. It provides examples of common solutes and solvents and explains how to determine which substance to treat as the solute based on the problem's specifications or relative quantities. The paragraph concludes with the calculation of molality for a solution with sodium hydroxide as the solute and water as the solvent, emphasizing the conversion from grams to kilograms for the solvent.

Mindmap

Keywords

💡Solution Concentration

Solution concentration refers to the amount of solute that is dissolved in a solvent. It is a critical concept in chemistry that helps in understanding the composition of solutions. In the video, various methods of expressing solution concentration, such as mass percent, volume percent, mole fraction, molality, and molarity, are discussed to illustrate different ways to quantify the concentration.

💡Solute

A solute is a substance that is dissolved within another substance, known as the solvent, to create a solution. In the context of the video, sodium chloride (salt) is given as an example of a solute that is dissolved in water, which acts as the solvent.

💡Solvent

The solvent is the substance that has the ability to dissolve other materials, known as solutes. Water is a common solvent and is used in the video to dissolve sodium chloride. The distinction between solute and solvent is fundamental to understanding how solutions are formed.

💡Mass Percent

Mass percent is a measure of the mass of the solute divided by the total mass of the solution, multiplied by 100 to get a percentage. It is used to express the concentration of a solute in a solution. In the video, it is calculated by dividing the mass of sodium chloride by the total mass of the solution (solute + solvent) and then multiplying by 100 to find the mass percent of sodium chloride in the solution.

💡Volume Percent

Volume percent, often denoted as v/v%, is the ratio of the volume of the solute to the total volume of the solution, multiplied by 100 to express it as a percentage. It is another way to quantify the concentration of a solute in a solution. The video explains that volume percent is calculated similarly to mass percent but uses volumes instead of masses.

💡Mole Fraction

Mole fraction is a way to express the concentration of a component in a mixture based on the number of moles of that component. It is calculated by dividing the number of moles of a particular substance by the total number of moles of all substances in the mixture. The video uses the mole fraction to illustrate the concentration of substances in a solution when multiple solutes are present.

💡Molarity

Molarity, represented by the symbol M, is the number of moles of solute per liter of solution. It is a common measure of solution concentration and is particularly useful for reactions in which the volume of the solution is significant. In the video, molarity is distinguished from molality and is calculated by dividing the moles of the solute by the volume of the solution in liters.

💡Molality

Molality, denoted by the lowercase 'm', is the concentration of a solution expressed as the number of moles of solute per kilogram of solvent. Unlike molarity, molality is independent of the volume of the solution and depends on the mass of the solvent. The video emphasizes the difference between molality and molarity, noting that molality uses the mass of the solvent in kilograms in the calculation.

💡Density

Density is a measure of mass per unit volume of a substance and is typically expressed in grams per milliliter (g/mL) or grams per cubic centimeter (g/cm³). In chemistry, it is used to convert between mass and volume, which is particularly useful when calculating the mass percent of a solute in a solution, as demonstrated in the video with the example of methanol and water.

💡Conversion Factors

Conversion factors are used in chemistry to change between different units of measurement. The video mentions common conversions such as 1 milliliter being equivalent to 1 cubic centimeter, and 1 liter being equal to 1000 milliliters or 1 kilogram being equal to 1000 grams. These conversions are essential for accurately calculating solution concentrations.

💡Mole

A mole is a fundamental unit in chemistry that represents the amount of a substance, defined as 6.022 x 10²³ particles (atoms, molecules, etc.). It is used to quantify the amount of solute in molarity and molality calculations. The video explains how to convert grams of a substance to moles using its molar mass, which is crucial for determining the concentration of solutions.

Highlights

The video focuses on solution concentration, covering concepts such as mass percent, volume percent, mole fraction, molality, and molarity.

The difference between solute and solvent is clarified, with sodium chloride as the solute and water as the solvent in the given example.

Mass percent is calculated as the mass of the solute divided by the mass of the solution, multiplied by 100 percent.

Volume percent is calculated as the volume of the solute divided by the volume of the solution, multiplied by 100.

Mole fraction is the moles of a particular substance divided by the total moles of all substances in the solution.

Molarity is defined as the moles of solute per liter of solution and is represented by the symbol M.

Molality differs from molarity in that it is moles of solute per kilogram of solvent, not the solution.

Density is defined as mass over volume and is typically given in grams per milliliter or grams per cubic centimeter.

A problem involving 15 grams of sodium chloride dissolved in 225 grams of water is used to demonstrate the calculation of mass percent.

A problem with 25 milliliters of methanol mixed with 150 milliliters of water illustrates the calculation of volume percent and mass percent.

The mole fraction of KCl in a solution with two moles of KCl dissolved in eight moles of water is calculated to be 0.2.

The mole fraction of sodium fluoride in a solution with 25 grams of sodium fluoride mixed with 200 grams of water is calculated to be approximately 0.051.

The molarity of a solution with 15 grams of sodium bromide dissolved in 400 milliliters is calculated to be 0.364 M.

The molality of a solution with 10 grams of sodium hydroxide dissolved in 500 grams of water is calculated to be 0.5 m.

A more complex problem involves calculating the molarity of a solution with a mass percent of AlCl3 and the density of the solution.

The molarity of the AlCl3 solution is calculated to be approximately 1.316 M, demonstrating the use of mass percent and density in solution concentration calculations.

The video emphasizes the importance of identifying the solute and solvent correctly, especially in cases where both substances can act as solvents.

Common solutes include salts like sodium chloride, potassium iodide, and sodium hydroxide, while common solvents include water, methanol, and ethanol.

The video provides a comprehensive overview of solution concentration calculations, offering clear explanations and examples for each concept.

Transcripts

Browse More Related Video

How to solve percent concentration problems even if you're 🤷🏻‍♀️ - Dr K

How to calculate percent concentration | Percent mass | Percent volume | Percent mass-volume - Dr K

Molarity versus Molality

Molarity Explained

What is molarity and molality Class 11? | What is molality and example? | calculate molality

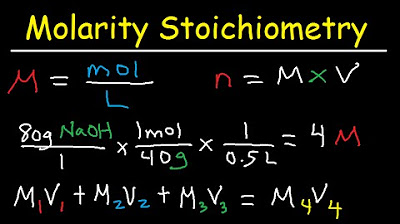
Molarity Dilution Problems Solution Stoichiometry Grams, Moles, Liters Volume Calculations Chemistry

Related Tags

Solution Concentration Chemistry Basics Mass Percent Volume Percent Mole Fraction Molarity Molality Density Solute Solvent Chemical Calculations