Calculating Power |Physics | Power formula

MooMooMath and Science
14 Dec 202105:00
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces viewers to the concept of power in the context of physics, explaining it as work divided by time. It uses practical examples involving activities like riding a bike up a hill and pushing a sled to demonstrate how to calculate power, the duration of work application, and the amount of work done. The script emphasizes the importance of understanding the relationships between work, power, and time, and concludes with a reminder to spread kindness.

Takeaways
  • 📚 Power is calculated using the formula: Power = Work / Time.
  • 🚴‍♂️ To find Power, use the formula and divide the given work by the time it was applied.
  • ⏳ If you need to calculate Time, divide the Work by the Power.
  • 🔧 To determine Work, multiply Power by Time.
  • 🌟 Example 1: 1224 Joules of work applied over 18 seconds results in 68 Watts of power.
  • 🛷 Example 2: 500 Joules of work applied over 25 seconds results in 20 Watts of power.
  • 🚵‍♂️ Example 3: To produce 1440 Joules with 180 Watts of power, it takes 8 seconds.
  • 🔄 Unit conversion: When calculating, ensure that the units of measure are consistent and cancel out appropriately.
  • 🌐 Understanding the relationship between Work, Power, and Time is crucial for solving these types of problems.
  • 💡 The concept of 'watts' is a measure of power, equivalent to joules per second.
  • 🌈 Kindness reminder: The video script concludes with a message of kindness, emphasizing the importance of being kind to others.
Q & A

  • What is the formula for calculating power?

    -The formula for calculating power is work divided by time.

  • How can you find the power if you know the work and time?

    -To find the power when you know the work and time, you divide the work (in joules) by the time (in seconds).

  • What is the unit of power?

    -The unit of power is watts, which is equivalent to joules per second (J/s).

  • How do you calculate the time required to apply a force if you know the work and power?

    -To calculate the time required, you divide the work (in joules) by the power (in watts).

  • In the example with the bike pedal, how much power is produced when 1224 joules of work are applied over 18 seconds?

    -When 1224 joules of work are applied over 18 seconds, the power produced is 68 watts (1224 J / 18 s = 68 W).

  • How much power was produced when John applied 500 joules of work for 25 seconds?

    -When John applied 500 joules of work for 25 seconds, the power produced was 20 watts (500 J / 25 s = 20 W).

  • If 180 watts of power is applied to a bike pedal, how much time is needed to produce 1440 joules of work?

    -With 180 watts of power applied, it would take 8 seconds to produce 1440 joules of work (1440 J / 180 W = 8 s).

  • What is the amount of work generated when 25 watts of power is applied to a machine for 20 seconds?

    -When 25 watts of power is applied to a machine for 20 seconds, the amount of work generated is 500 joules (25 W * 20 s = 500 J).

  • Why is it important to consider units of measure when calculating power, work, and time?

    -Considering units of measure is crucial because it ensures the accuracy of the calculations and helps maintain the correct relationships between the physical quantities involved.

  • How does the concept of power relate to everyday activities like riding a bike or pushing a sled?

    -The concept of power relates to everyday activities as it quantifies the rate at which work is done. For instance, the more power you apply while riding a bike or pushing a sled, the faster you can perform the task or cover the distance.

  • What message does the video script conclude with regarding kindness?

    -The video script concludes with a reminder to practice kindness, emphasizing that kindness multiplies and encourages the viewer to be kind to someone that day.

Outlines
00:00
📘 Introduction to Power Calculation

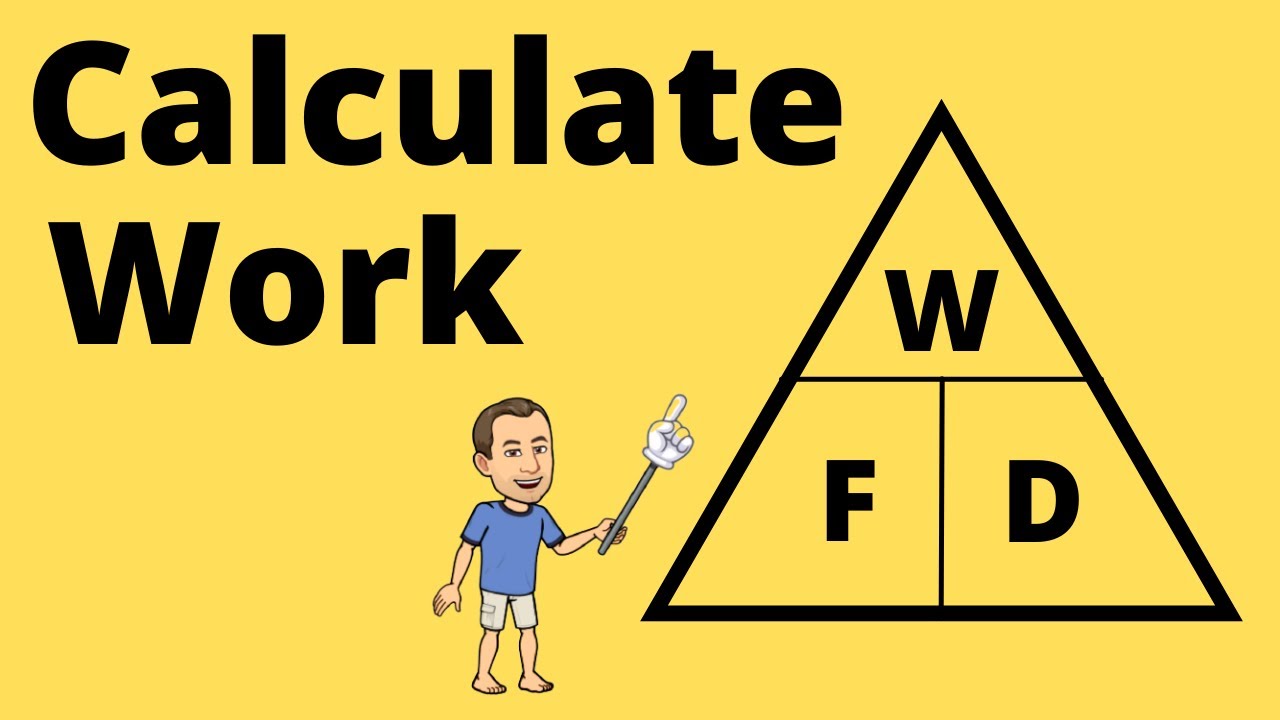
This paragraph introduces the concept of power in the context of movie math and science. It explains the formula for calculating power, which is work divided by time. The paragraph further elaborates on how to use this formula to determine power, time, and work by providing a triangle method for better understanding. It sets the stage for the practical examples that will be discussed later in the video, emphasizing the importance of understanding these basic concepts before diving into the calculations.

🚴‍♂️ Calculating Power with Bike Pedaling

This paragraph presents a practical example of calculating power by considering a scenario where work is applied to bike pedals while riding up a hill. It provides specific values of work (1224 joules) and time (18 seconds), and then demonstrates how to use the power formula to calculate the power produced. The paragraph also explains the importance of ensuring the correct units of measurement, resulting in 68 watts of power produced in this example. This segment aims to clarify the application of the power formula in real-life situations and the significance of units in calculations.

🏋️‍♂️ John's Sled Pushing Power

In this paragraph, the video script introduces another example involving John applying work to push a sled. The values given are 500 joules of work done over a period of 25 seconds. The paragraph explains how to calculate the power produced in this scenario, leading to a result of 20 watts. This example further reinforces the concept of power and emphasizes the method of calculation, providing viewers with a clear understanding of how to apply the power formula in different contexts.

🚴‍♀️ Time Needed for Specific Work with Given Power

This paragraph focuses on calculating the time required to produce a specific amount of work when a known power is applied. Using the example of 1440 joules of work and an input power of 180 watts, the video script walks through the process of finding the time needed. The explanation includes a detailed breakdown of how to manipulate the units of measurement to arrive at the correct result, which is 8 seconds. This part of the video aims to deepen the viewer's understanding of the relationship between work, power, and time.

⚙️ Work Generated by Constant Power

The final paragraph discusses the calculation of work generated when a constant power is applied for a certain period. Using the example of 25 watts of power applied over 20 seconds, the video script shows how to calculate the resulting work. The explanation includes a step-by-step breakdown of the multiplication process and the cancellation of units, leading to a result of 5000 joules. This example serves to solidify the viewer's grasp of the power formula and its applications, while also emphasizing the importance of accurate unit handling in calculations.

Mindmap
Keywords
💡Power
Power is a physical quantity that represents the rate at which work is done or energy is transferred. In the context of the video, it is defined by the formula Power = Work / Time. It is a crucial concept as it helps in understanding the efficiency of energy usage. For example, the video demonstrates how to calculate the power produced when 1224 joules of work are applied over 18 seconds, resulting in 68 watts.
💡Work
Work in physics is the measure of energy transfer that occurs when an object is moved by applying force along a displacement. In the video, work is used to calculate power and is measured in joules. The script provides an example of 1224 joules of work done while riding a bike up a hill, emphasizing the relationship between work, power, and time.
💡Time
Time is the continuous progression of existence and events, used to sequence actions and determine durations. In the context of the video, time is one of the key components in the power calculation formula. It is used to determine how long an action takes to perform, as seen in the examples where 18 seconds and 25 seconds durations are critical to calculating power outputs.
💡Formula
A formula is a mathematical statement that expresses a relationship between quantities. In the video, the formula for power is central to understanding the calculations. The formula Power = Work / Time is used to solve for power, time, or work depending on the given values, as demonstrated in the various examples throughout the script.
💡Joules
Joules are the unit of measurement for work and energy in the International System of Units (SI). In the video, work is measured in joules, and this unit is used in all the calculations to determine power. Understanding the concept of joules is essential to grasp how much energy is being transferred or work being done, as in the example of 1224 joules of work applied to the bike pedal.
💡Watts
Watts are the units used to measure power, which is the rate of doing work or the rate of energy transfer. In the video, power is often expressed in watts, and the script provides examples of calculating power in watts, such as when 1224 joules of work are done in 18 seconds resulting in a power output of 68 watts.
💡Calculation
Calculation refers to the process of performing mathematical operations to solve for unknown values. In the video, calculations are central to understanding and applying the power formula. Each example in the script involves performing calculations to determine power, work, or time based on the given values and the formula Power = Work / Time.
💡Efficiency
Efficiency is the measure of how well a process converts input to desired output with minimal waste. While not explicitly mentioned in the script, the concept of efficiency underlies the discussion of power, as it relates to how effectively energy is used. By calculating power, one can assess the rate at which work is done and potentially identify more efficient methods of energy usage.
💡Physics
Physics is the natural science that studies matter, its motion, and the forces that act upon it. The video's content is rooted in physics, as it deals with concepts of work, power, and energy, which are fundamental topics in physics. Understanding the physics behind these calculations helps in applying the formulas in real-world scenarios, such as calculating the power output when riding a bike up a hill.
💡Energy
Energy is the capacity to do work or the ability to cause change. It is a fundamental concept in physics and is closely related to the topics of work and power discussed in the video. Energy, in the form of joules, is transferred or converted during work, and power represents the rate at which this energy is utilized. The script's examples illustrate how energy is calculated and understood in terms of work and power.
💡Mechanics
Mechanics is a branch of physics that deals with the motion of objects and the forces that cause these motions. The video's focus on work, power, and energy is directly related to mechanics, as these concepts are essential to understanding and analyzing the motion of objects, such as a bike being ridden up a hill or a sled being pushed.
Highlights

The video introduces the concept of calculating power, which is crucial in understanding various physical phenomena.

The formula for power is given as work divided by time, a fundamental principle in physics.

The video presents a practical application of power calculation by using a real-world example of riding a bike up a hill.

An example calculation shows that 1224 joules of work applied over 18 seconds results in 68 watts of power.

Another example demonstrates how to calculate the power produced when John applies 500 joules of work over 25 seconds, resulting in 20 watts.

The video explains how to find the time needed to produce a certain amount of work using the relationship between work, power, and time.

A specific example given is calculating the time needed to produce 1440 joules of work with 180 watts applied to a bike pedal, which is 8 seconds.

The video emphasizes the importance of understanding units of measurement and how they interact in calculations, such as joules divided by seconds yielding watts.

Another scenario presented is calculating the amount of work generated when a machine is powered by 25 watts for 20 seconds, producing 5000 joules.

The video uses a triangle to visually represent the relationship between power, time, and work, aiding in understanding and problem-solving.

The concept of power is not only academic but also has practical applications in everyday activities like biking and pushing a sled.

The video provides a step-by-step guide on how to approach problems involving power, work, and time, making complex concepts more accessible.

The video stresses the importance of unit consistency and conversion in solving physics problems, ensuring accurate results.

The video concludes with a reminder to practice kindness, highlighting the value of compassion in everyday life.

The video is an educational resource that combines theoretical knowledge with practical examples to enhance learning.

The video's approach to teaching power, work, and time is engaging and informative, suitable for a wide range of audiences.

Transcripts

Browse More Related Video

Work and Power in Physics

What Is Power? | Physics in Motion

How to Calculate Work Done | Physics | Work = Force x Distance

Calculating Power in Physics: Example Problems

High School Physics - Power

Work, Energy, & Power - Formulas and Equations - College Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsWork CalculationPower FormulaTime ManagementEducational ContentMath and SciencePractical ExamplesWattage UnderstandingEnergy DynamicsMechanical Work