Zero matrix | Matrices | Precalculus | Khan Academy

Khan Academy
17 Mar 201404:41
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explores the concept of identity and zero matrices in the context of traditional multiplication and its analogy to matrix multiplication. It explains how multiplying any matrix by an identity matrix results in the original matrix, and how a zero matrix, when multiplied with any matrix, yields a zero matrix with potentially different dimensions. The script encourages viewers to visualize and verify these concepts through examples, highlighting the importance of understanding matrix dimensions in the process.

Takeaways
  • 🚀 The concept of identity in multiplication is analogous to the identity matrix in matrix multiplication.
  • 🔢 Multiplying any matrix by an identity matrix results in the original matrix, demonstrating the identity property.
  • 📏 Identity matrices have the same dimensions as the square matrix they are multiplied with.
  • 🔄 Non-square matrices require different identity matrices based on their dimensions for the identity property to hold.
  • ⏺ The number 0 in traditional multiplication has an analogous counterpart in matrix multiplication: the 0 matrix.
  • 🎯 A 0 matrix, when multiplied by any matrix, results in another 0 matrix.
  • 🔢 The resulting 0 matrix from multiplication may have different dimensions than the original matrices involved.
  • 🔍 The dot product of rows and columns in a 0 matrix will always yield 0, maintaining the 0 matrix structure.
  • 🧠 Understanding the properties of 0 and identity matrices is crucial for grasping matrix multiplication fundamentals.
  • 🔍 Verifying the results of matrix multiplication with 0 matrices can reinforce the understanding of these properties.
  • 📚 The script provides a practical example of multiplying a non-square matrix with a 0 matrix to produce a 0 matrix with different dimensions.
Q & A

  • What is the identity property of traditional multiplication?

    -The identity property of traditional multiplication states that when you multiply any number by 1, you get that number again. In other words, 1 is the identity number because it does not change the value of the other number it is multiplied by.

  • What inspired the concept of identity matrices?

    -The concept of identity matrices was inspired by the identity property of traditional multiplication. The idea is that there might exist matrices which, when multiplied by another matrix, will result in the original matrix.

  • What happens when a matrix is multiplied by an identity matrix?

    -When a matrix is multiplied by an identity matrix, the original matrix is obtained again. This is true whether the matrix is multiplied by the identity matrix from the left or the right.

  • What are the conditions for two matrices to be multiplied?

    -For two matrices to be multiplied, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting product will have the number of rows of the first matrix and the number of columns of the second matrix.

  • How does the identity matrix differ for non-square matrices?

    -For non-square matrices, there are two different identity matrices depending on the appropriate dimensions. One is the result of multiplying the matrix by an identity matrix with the same number of rows as the original matrix, and the other is with an identity matrix with the same number of columns.

  • What is the analogy of 0 in matrix multiplication?

    -In matrix multiplication, the analogy of 0 is a zero matrix. Multiplying any matrix by a zero matrix results in a zero matrix, where all the entries are 0.

  • What is a zero matrix and how does it relate to matrix multiplication?

    -A zero matrix is a matrix where all the entries are 0. In matrix multiplication, a zero matrix plays a role similar to that of 0 in traditional multiplication, as it will result in a zero matrix when multiplied by any other matrix.

  • How does the dimension of a zero matrix affect the result of matrix multiplication?

    -The dimension of a zero matrix must match the number of columns of the first matrix and the number of rows of the second matrix for the multiplication to be valid. The resulting zero matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.

  • What happens when a 2x3 matrix is multiplied by a 3x2 zero matrix?

    -When a 2x3 matrix is multiplied by a 3x2 zero matrix, the resulting product will be a 3x3 zero matrix, where all the entries are 0. This is because each entry in the resulting matrix is the sum of products of the corresponding entries, all of which are 0.

  • How can you verify that all entries in the resulting matrix of a zero matrix multiplication are 0?

    -To verify that all entries in the resulting matrix are 0, you can perform the matrix multiplication step by step, calculating each entry by taking the dot product of the corresponding row of the first matrix with the column of the second matrix. Since all entries of the zero matrix are 0, the dot product will also be 0, leading to a resulting zero matrix.

  • What is the significance of understanding the identity and zero matrices in linear algebra?

    -Understanding the identity and zero matrices is crucial in linear algebra as they play fundamental roles in matrix operations. The identity matrix is essential for understanding how certain operations leave a matrix unchanged, while the zero matrix is important for understanding how certain operations can result in a matrix with no effect or influence.

Outlines
00:00
📊 Introduction to Analogies in Multiplication and Identity Matrices

The paragraph introduces an analogy between traditional scalar multiplication and matrix multiplication, focusing on the concept of identity. It explains that just as multiplying any number by 1 yields the same number, there exist identity matrices that, when multiplied by another matrix, yield the same matrix. The identity matrix is shown to be applicable to square matrices, with different matrices required for non-square matrices based on their dimensions. The concept is extended to include the zero matrix, which, when multiplied by any matrix, results in a zero matrix with potentially different dimensions.

Mindmap
Keywords
💡Analogies
Analogies are comparisons made between two things that are not necessarily alike but share some common characteristics. In the context of the video, analogies are drawn between traditional multiplication and matrix multiplication to help viewers understand the concepts of identity and zero matrices. For example, just as the number 1 is the identity in traditional multiplication, the identity matrix plays a similar role in matrix multiplication.
💡Scalar Multiplication
Scalar multiplication refers to the process of multiplying a scalar (a single number) by a vector or matrix. In the video, the concept is used to introduce the idea that multiplying by the identity (1 or 0, depending on the context) results in the same value or matrix, which is a fundamental property in both traditional and matrix multiplication.
💡Identity Matrices
An identity matrix is a special type of square matrix with ones on the diagonal and zeros elsewhere, such that when any matrix is multiplied by the identity matrix, the original matrix is returned. The video uses the concept of identity matrices to illustrate how certain matrices can act as an 'identity' in the context of matrix multiplication, just as the number 1 does in traditional multiplication.
💡Zero Matrix
A zero matrix is a matrix in which all the elements are zero. In the context of the video, the zero matrix is analogous to the number 0 in traditional multiplication, where multiplying any matrix by a zero matrix results in a zero matrix, regardless of the original matrix's dimensions.
💡Matrix Multiplication
Matrix multiplication is a binary operation that takes a pair of matrices and produces another matrix. The video script uses this concept to explain how certain matrices, like the identity and zero matrices, behave in multiplication, drawing parallels with traditional scalar multiplication.
💡Dimensions
Dimensions in the context of matrices refer to the number of rows and columns a matrix has. The script emphasizes the importance of compatible dimensions for matrix multiplication, where the number of columns in the first matrix must equal the number of rows in the second matrix for the multiplication to be valid.
💡Identity Property
The identity property is a fundamental property in mathematics stating that when a value (like a number or a matrix) is multiplied by the identity element (like 1 or an identity matrix), the original value is returned. The video script uses this property to explain how the identity and zero matrices behave in multiplication, serving as the 'identities' for matrices.
💡Dot Product
The dot product, also known as the scalar product, is an operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number. In the context of the video, the dot product is used to describe the process of multiplying corresponding elements of two matrices and summing the results to get the entries of the resulting matrix.
💡Traditional Multiplication
Traditional multiplication refers to the basic arithmetic operation of multiplying two numbers together. The video script uses the principles of traditional multiplication to introduce and explain more complex concepts like matrix multiplication, identity matrices, and zero matrices.
💡Zero
In mathematics, zero is the additive identity, meaning that adding zero to any number does not change the value of that number. The video script extends this concept to matrix multiplication, where a zero matrix, when multiplied by any matrix, results in a zero matrix.
💡3x2 Matrix
A 3x2 matrix is a matrix with three rows and two columns. In the video, the script uses the example of a 3x2 matrix to illustrate the process of matrix multiplication and the resulting dimensions of the product matrix.
Highlights

Analogy between traditional multiplication and scalar multiplication is discussed.

The identity property of multiplication is introduced, where multiplying by 1 returns the original number.

Identity matrices are explored, which when multiplied by another matrix, return the original matrix.

The concept of identity matrices is shown to be dependent on the matrix being square.

Different identity matrices exist based on the dimensions of the matrices involved.

Analogy between the number 0 in traditional multiplication and a 0 matrix in matrix multiplication is made.

A 0 matrix, when multiplied by any matrix, results in a 0 matrix.

The resulting 0 matrix may have different dimensions than the original matrix.

An example is provided where the matrix [1,2,3,4] is multiplied by a 0 matrix to yield a 0 matrix.

The dot product of rows and columns in the 0 matrix results in zeros.

A second example is given with a matrix [1,2,3,4,5,6] and a 0 matrix with different dimensions.

The 0 matrix for the second example has dimensions 3x2 to match the rows and columns for multiplication.

The resulting product of the second example is a 3x3 matrix with all entries being 0.

The multiplication process is explained, showing that every entry in the resulting matrix is 0.

The example illustrates the concept of a 0 matrix multiplying with a non-zero matrix to produce a 0 matrix with different dimensions.

Transcripts

Browse More Related Video

Identity matrix | Matrices | Precalculus | Khan Academy

Dimensions of identity matrix | Matrices | Precalculus | Khan Academy

Idea behind inverting a 2x2 matrix | Matrices | Precalculus | Khan Academy

PreCalculus - Matrices & Matrix Applications (19 of 33) What is an Identity Matrix?

Matrix Multiplication and Associated Properties

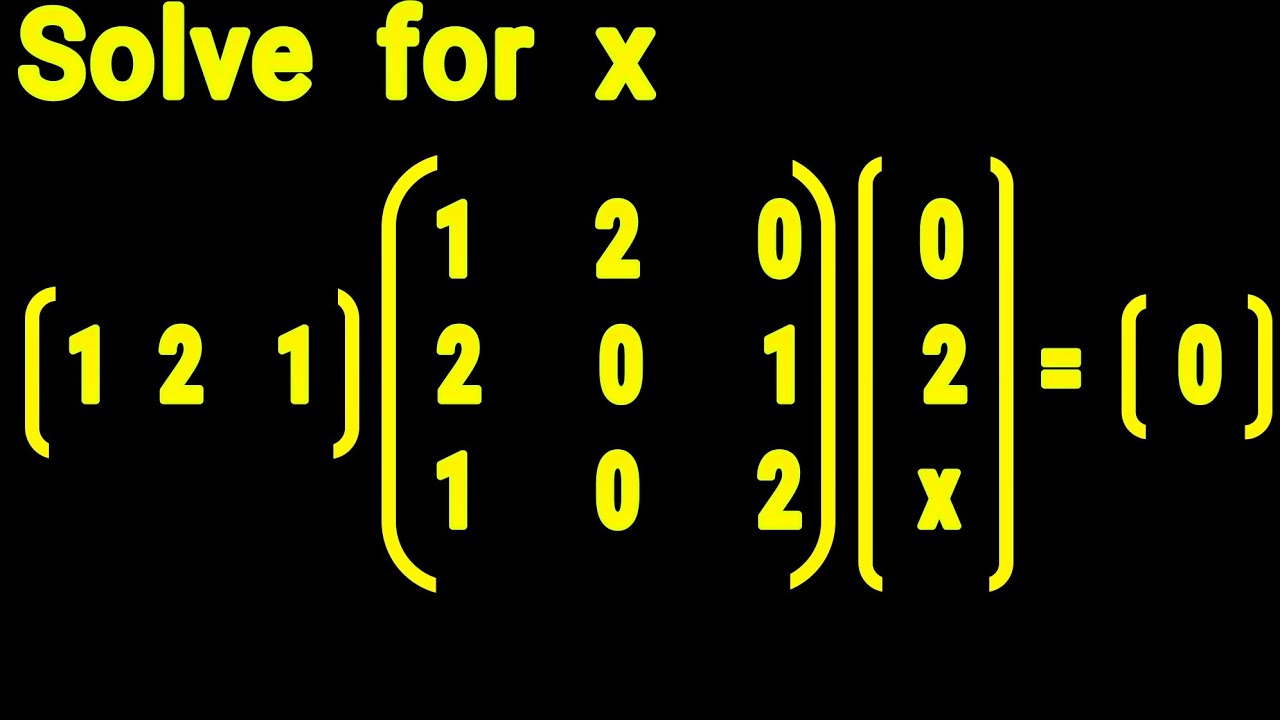
Solve for x | Matrix Multiplication

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Matrix MultiplicationIdentity MatricesZero MatricesMathematicsLinear AlgebraEducational ContentMath AnalogiesScalar MultiplicationMatrix PropertiesMath Tutorial