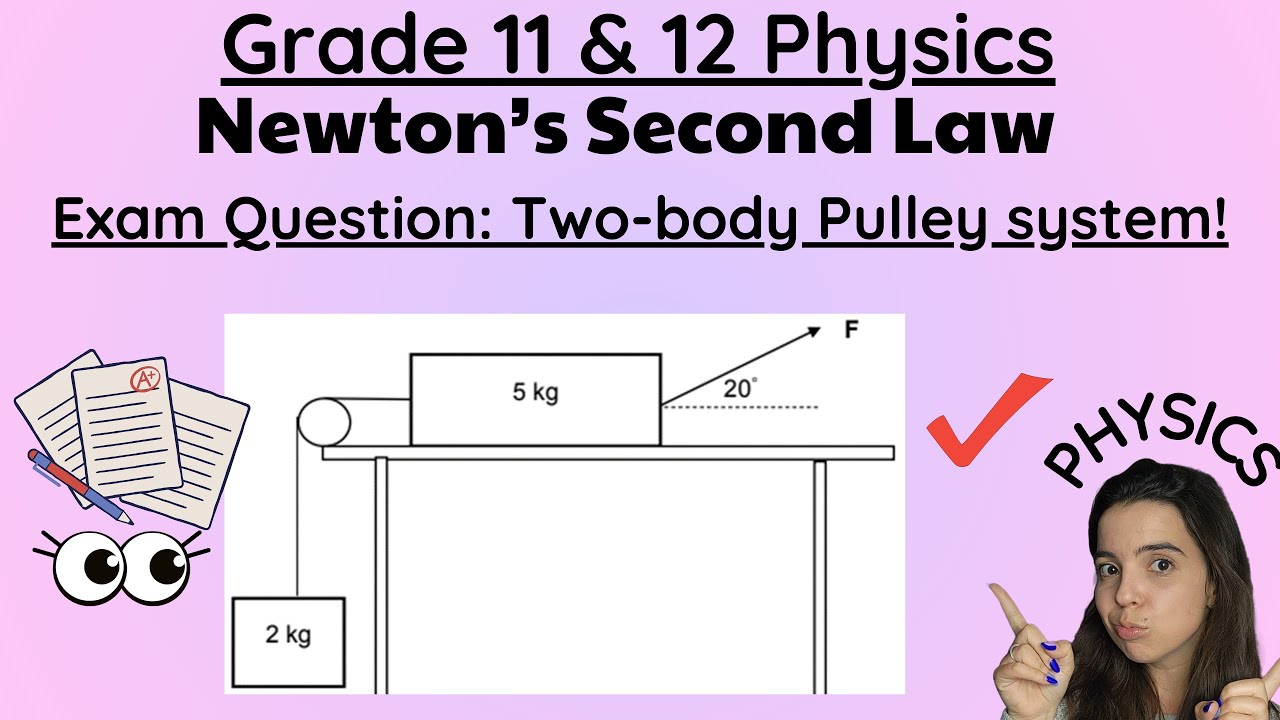
AP Physics - Atwood Machines

Dan Fullerton
26 Sept 201206:29
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, Dan Fullerton introduces the concept of Atwood machines, which are essential for understanding the constant tension in a light string passing over a massless pulley. The video's primary objectives are to help students analyze the motion of a two-object system connected by a string and to solve problems involving Newton's laws that result in simultaneous linear equations. By using clear examples and step-by-step explanations, Fullerton demonstrates how to set up and solve these problems, ultimately enhancing the viewer's comprehension of these fundamental physics concepts.

Takeaways
  • 📚 The Atwood machine is a lab apparatus consisting of two masses, m1 and m2, connected by a string over a massless, frictionless pulley.
  • 🎯 The key concept is that the tension in the string is constant, allowing for the analysis of the motion of the system of two objects.
  • 📈 Newton's second law is applied to solve problems involving the system, leading to simultaneous linear equations with unknown forces or accelerations.
  • 🔄 The setup assumes ideal conditions: massless string, no friction, and no inertia from the pulleys.
  • 🧭 A positive direction must be chosen to analyze the motion, with one object moving up (positive) and the other down (negative).
  • 📊 Freebody diagrams are used to analyze each mass separately, applying Newton's second law to determine the forces acting on each.
  • 🔧 The tension in the string can be expressed in terms of the masses' accelerations and gravitational forces, leading to an equation for the system.
  • 🌐 Two methods are presented for solving the system: analyzing each mass individually or considering the system as a whole.
  • 📝 The acceleration of the system can be calculated using the formula: a = (G * (m1 - m2)) / (m1 + m2), where G is the acceleration due to gravity.
  • 📚 The Atwood machine is relevant to AP Physics B and C objectives, providing a context for understanding and applying fundamental physics concepts.
  • 💡 The video encourages further exploration of Atwood machines and related physics topics through additional resources like 'a plus physics comm'.
Q & A

  • What is the primary purpose of discussing Atwood machines in the context of this lesson?

    -The primary purpose is to introduce students to the concept that tension is constant in a light string passing over a massless pulley, and to use this fact to analyze the motion of a system of two objects joined by a string.

  • What are the key objectives of this lesson on Atwood machines?

    -The key objectives are to analyze the motion of a system of two objects joined by a string and to solve problems where applications of Newton's laws lead to simultaneous linear equations involving unknown forces or accelerations.

  • What is an Atwood machine?

    -An Atwood machine is a lab apparatus or experimental setup where two objects of mass m1 and m2 are connected by a light, massless string to an ideal, massless pulley.

  • What assumptions are made in the properties of an Atwood machine?

    -The assumptions include that the pulleys are ideal, meaning they are frictionless, massless, and have no inertia added to the system. Additionally, the tension in the light string over the ideal pulley is constant.

  • How does one set up a problem involving an Atwood machine?

    -To set up such a problem, the first step is to decide on a direction to call positive. Then, analyze each mass separately using Newton's second law and freebody diagrams.

  • How does the speaker suggest choosing a positive direction in an Atwood machine problem?

    -The speaker suggests choosing a consistent direction and calling it the positive direction, typically based on the observed motion of the objects, with one object moving up and the other moving down.

  • What is the first Newton's second law equation written in the script, and for which mass was it written?

    -The first Newton's second law equation written in the script is for mass m2, and it is T - m2g = m2a, where T is the tension, m2 is the mass of the second object, g is the acceleration due to gravity, and a is the acceleration.

  • How is the tension in the string related to the acceleration of the system?

    -The tension in the string is equal to the mass of the second object times its acceleration plus the mass of the second object times the acceleration due to gravity.

  • What is the second Newton's second law equation written in the script, and for which mass was it written?

    -The second Newton's second law equation written in the script is for mass m1, and it is m1g - T = m1a, where m1 is the mass of the first object, g is the acceleration due to gravity, T is the tension, and a is the acceleration.

  • How can the acceleration of the system be found by analyzing the system as a whole?

    -By analyzing the system as a whole and applying Newton's second law, the acceleration can be found using the equation G(m1 - m2) = (m1 + m2)a, where G is the acceleration due to gravity, m1 and m2 are the masses of the objects, and a is the acceleration of the system.

  • What is an alternate method to solve for the system's acceleration mentioned in the script?

    -An alternate method mentioned in the script is to analyze the entire system as a closed system and apply Newton's second law directly, which leads to the same equation for the system's acceleration: a = G(m1 - m2) / (m1 + m2).

Outlines
00:00
📚 Introduction to Atwood Machines and Problem Setup

This paragraph introduces the concept of Atwood machines, which are experimental setups used to demonstrate the constant tension in a light string passing over a massless pulley. The main objective is to use this principle to analyze the motion of a system with two objects connected by a string. The video aims to help students understand how to solve problems involving Newton's laws that result in simultaneous linear equations with unknown forces or accelerations, aligning with AP Physics B and C objectives. The setup involves two objects of masses m1 and m2 connected by a string, with the assumption that the pulley is ideal (frictionless and massless), leading to constant tension throughout the string.

05:00
🔍 Analyzing the System and Newton's Second Law

In this paragraph, the speaker explains how to set up and analyze problems involving Atwood machines using Newton's second law. The process begins by defining a positive direction for the analysis. The speaker chooses the direction where one object moves up and the other down as the positive direction. Using Freebody diagrams and Newton's second law, the speaker analyzes each mass separately to write equations for the net force acting on each mass. The equations are then solved to find the acceleration of the system. An alternative method is also discussed, where the entire system is considered as a closed system, and Newton's second law is applied to find the overall acceleration. The speaker emphasizes that both methods yield the same result, providing a comprehensive understanding of how to approach Atwood machine problems.

Mindmap
Keywords
💡Atwood Machine
An Atwood Machine is a simple experimental setup used in physics to study the motion of two masses connected by a string passing over a pulley. In the context of the video, it is a key tool for demonstrating and analyzing the principles of mechanics, particularly those related to tension and acceleration in a system of two objects. The video script describes how the Atwood Machine allows for simple calculations due to its idealized assumptions, such as massless pulleys and a constant tension in the string.
💡Tension
In the context of the video, tension refers to the force exerted by the string on the objects in an Atwood Machine. It is a key concept because the tension in the string is assumed to be constant, which simplifies the analysis of the system's motion. Tension is a reaction to the weights of the objects and is crucial in applying Newton's laws to solve for the motion of the system.
💡Newton's Laws
Newton's Laws are fundamental principles of classical mechanics that describe the relationship between the motion of an object and the forces acting upon it. In the video, Newton's Laws are applied to analyze the motion of the two-mass system in the Atwood Machine, leading to the formulation of simultaneous linear equations to solve for unknown forces and accelerations.
💡Freebody Diagram
A Freebody Diagram is a graphical representation that shows all the forces acting on an object, helping to visualize and analyze the motion of the object. In the video, Freebody Diagrams are used to break down the forces acting on each mass in the Atwood Machine, which is essential for applying Newton's second law to find the acceleration of the system.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a central concept in the video as it is the unknown quantity that the viewer is trying to solve for using the Atwood Machine. By applying Newton's second law, the video demonstrates how to calculate the acceleration of the system of two masses connected by a string.
💡Mass
Mass is a measure of the amount of matter in an object, and it is a fundamental property that determines the object's response to forces according to Newton's laws. In the video, the Atwood Machine involves two objects with masses m1 and m2, and the analysis involves understanding how these masses interact under the influence of gravity and tension.
💡Pulley
A pulley is a wheel with a grooved rim that is used to change the direction of a force applied to it, often through the use of a string or rope. In the context of the Atwood Machine, the pulley is assumed to be ideal, meaning it is massless and frictionless, which simplifies the analysis of the system by eliminating the need to consider the pulley's inertia or additional forces.
💡Linear Equations
Linear Equations are mathematical statements that assert the equality of two expressions, each of which is a linear combination of variables. In the video, the application of Newton's laws leads to the formation of simultaneous linear equations with unknown forces and accelerations, which are then solved to analyze the motion of the Atwood Machine.
💡Positive Direction
The positive direction is a chosen convention in which an increase in a particular quantity, such as position or velocity, is considered positive. In the video, selecting a positive direction is crucial for applying Newton's second law and setting up the equations to solve for the motion of the two masses in the Atwood Machine.
💡Frictionless
Frictionless refers to a condition where there is no resistance to motion between surfaces in contact. In the idealized Atwood Machine described in the video, the pulley is assumed to be frictionless, meaning it does not introduce any resistive forces that would affect the motion of the masses, simplifying the analysis of the system.
💡Gravitational Acceleration (g)
Gravitational acceleration, denoted by 'g', is the acceleration due to Earth's gravity, which causes objects to experience a force pulling them toward the center of the Earth. In the video, gravitational acceleration is a key factor in the equations used to analyze the motion of the masses in the Atwood Machine, as it represents the weight of the objects and influences their acceleration.
Highlights

Introduction to Atwood machines and their educational purpose.

Tension is constant in a light string passing over a massless pulley.

Using the constant tension to analyze the motion of a system of two objects joined by a string.

Solving problems involving Newton's laws that lead to simultaneous linear equations.

Atwood machine as a lab apparatus with two objects of mass m1 and m2 connected by a string.

Properties of an Atwood machine: ideal, frictionless, and massless pulleys.

Setting a positive direction for problem-solving consistency.

Analyzing each mass separately using Newton's second law and Freebody diagrams.

Writing Newton's second law equations for each mass in the Y direction.

Solving for tension in the system using Newton's second law equations.

Rearranging the equations to solve for the system's acceleration.

Alternate method of solving by analyzing the system as a whole.

Newton's second law applied to the entire system for a different perspective.

Deriving the same result for acceleration using the alternate method.

Atwood machines' relevance to AP Physics B and AP Physics C objectives.

The importance of understanding Atwood machines for academic and practical applications.

Resource recommendation for further help and information on Atwood machines.

Transcripts

Browse More Related Video

Incline Plane Problems with Friction

Newton's Second Law Exam Question: Two-body systems Pulley practice

AP Physics 1 2016 Free Response Solutions

2015 AP Physics 1 Free Response #1

AP Physics 1 - Air Resistance

Partial Fraction Decomposion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EducationMechanical SystemsAtwood MachineNewton's LawsTension AnalysisProblem SolvingLab ApparatusFrictionless PulleysMass MotionAP Physics