Volume of Revolution via Shells | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare
7 Jan 201108:32
EducationalLearning
32 Likes 10 Comments

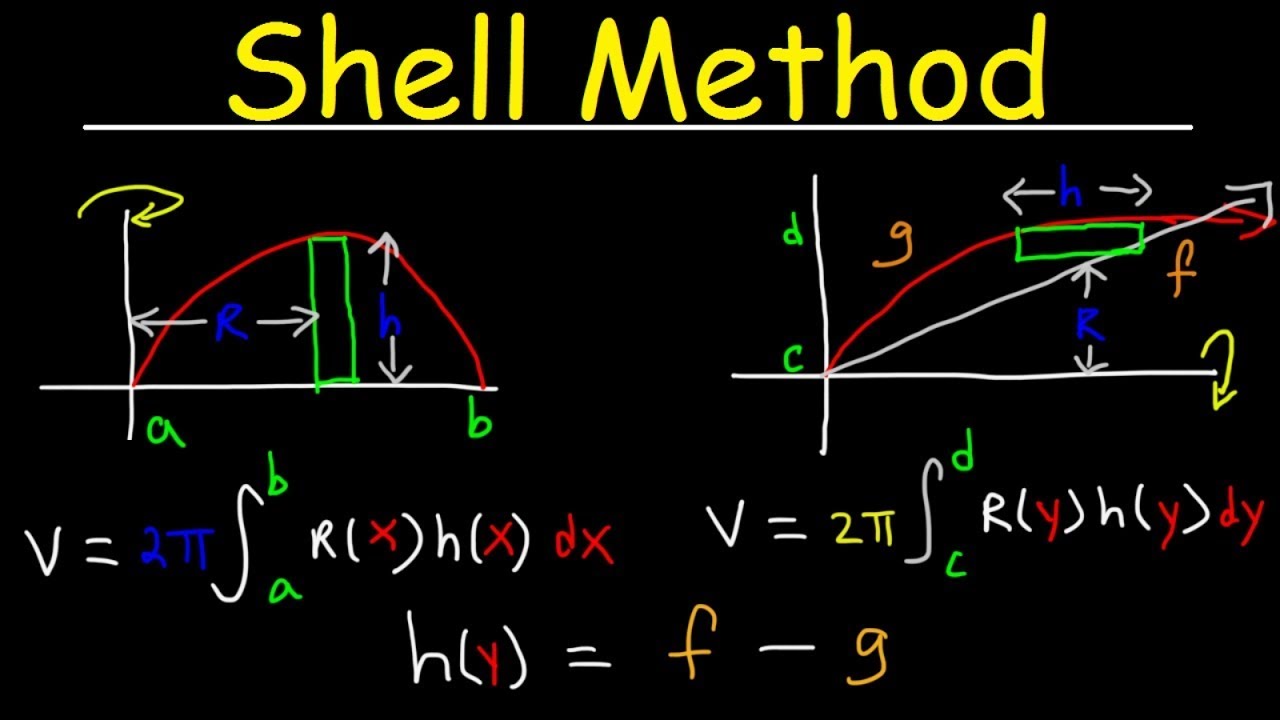
TLDRIn this educational video, the professor guides students through a solid of revolution problem, focusing on finding the volume of a solid formed by rotating a region bounded by y=0, x=4, and y=√x around the line x=6. The professor emphasizes sketching the region and choosing the shell method for simplicity, explaining the process of determining the radius and height as functions of x. The method involves setting up an integral with 2Ο€*r*h, where r is the distance from the rotation line and h is the curve's height, and solving it to find the volume.

Takeaways
  • πŸ“š The video is a recitation on finding the volume of a solid of revolution.
  • πŸ“ The problem involves rotating a region bounded by y=0, x=4, and y=√x around the line x=6.
  • 🎨 The first step is to sketch the two-dimensional region and understand the rotation line's position relative to it.
  • πŸ” A rough sketch helps visualize the region and the rotation line without needing a full 3D picture.
  • πŸ“ The rotation line x=6 is offset from the region, creating a gap that affects the calculation method.
  • πŸŒ€ The professor prefers the shell method for this problem due to its simplicity in handling the gap.
  • πŸ“‰ The height (h) of the shell is determined by the curve y=√x, making h=√x.
  • πŸ“Œ The radius (r) is the distance from the rotation line x=6 to the curve, which is 6-x.
  • βš™οΈ The integral for the volume is set up using 2Ο€rh, integrating from x=0 to x=4.
  • πŸ“ The integral involves the expression 2Ο€(6-x)√x dx, which is simplified and solved for the volume.
  • πŸ›  The power rule is used for integration, and the final volume is evaluated to get a numerical result.
Q & A

  • What is the main objective of the video?

    -The main objective of the video is to find the volume of the solid generated by rotating the region bounded by y=0, x=4, and y=√x around the line x=6.

  • What is the first step recommended by the professor when solving this problem?

    -The first step recommended by the professor is to get a rough sketch of the region that is being rotated to understand where the rotation line is with respect to that region.

  • What method does the professor choose to use for solving the problem?

    -The professor chooses to use the shell method for solving the problem.

  • Why does the professor prefer the shell method over the washer method for this particular problem?

    -The professor prefers the shell method because it does not require worrying about subtracting off pieces due to the gap in the region, as it is inherent in the radius determined by the x values chosen.

  • What is the formula used in the shell method for calculating the volume of a solid of revolution?

    -The formula used in the shell method is 2*pi*r*h, where r is the radius and h is the height of the shell.

  • How does the professor determine the height (h) of the shell?

    -The professor determines the height (h) as the function y=√x, since the curve being rotated is y=√x.

  • How does the professor determine the radius (r) of the shell?

    -The professor determines the radius (r) as the distance from the line of rotation (x=6) to the curve, which is 6 - x.

  • What is the range of x values for the integral when using the shell method?

    -The range of x values for the integral is from 0 to 4, as the region of interest is bounded by x=4.

  • Why is it important to consider the gap in the region when using the shell method?

    -It is important to consider the gap because it affects the determination of the radius, as the radius is the distance from the line of rotation to the curve, which includes the gap.

  • What does the professor suggest for students to do after explaining the method?

    -The professor suggests that students should finish and evaluate the integral to get the actual volume of the solid.

  • What is the significance of the rotating line being x=6 in the context of this problem?

    -The significance of the rotating line being x=6 is that it is the axis around which the region is rotated to form the solid, and it is also the reference point for determining the radius of the shells.

Outlines
00:00
πŸ“š Introduction to Solid of Revolution Problem

The professor begins by welcoming students back to the recitation and introduces a new problem involving the calculation of the volume of a solid of revolution. The problem involves rotating a region bounded by y=0, x=4, and y=√x around the line x=6. The professor emphasizes the importance of sketching the region and understanding the rotation line's position relative to it. The method of solving is left to the student's preference, but the professor hints at using the shell method for this particular problem.

05:02
πŸ“ Setting Up the Shell Method for Calculation

The professor proceeds to explain the shell method for solving the problem, focusing on the need to determine the radius and height in terms of x, given the rotation around the line x=6. The professor provides a rough sketch to visualize the region and the line of rotation, noting the gap between the region and the line. The radius is identified as the distance from the line of rotation (x=6) to the curve (x-value), resulting in the expression 6 - x. The height is determined by the function y=√x. The integral to calculate the volume is set up as 2Ο€ * (6 - x) * √x, integrated from x=0 to x=4. The professor simplifies the expression and suggests using the power rule for integration, inviting students to complete the calculation for the final volume.

Mindmap
Keywords
πŸ’‘Solid of Revolution
A 'Solid of Revolution' is a three-dimensional geometric shape created by rotating a two-dimensional area around an axis. In the video, the professor is discussing how to find the volume of such a solid generated by rotating a specific region bounded by certain curves around the line x equals 6. This concept is central to the video's theme of calculating volumes in calculus.
πŸ’‘Volume
Volume refers to the amount of space occupied by a solid object. In the context of the video, the professor is focusing on calculating the volume of a solid of revolution, which is a fundamental concept in integral calculus. The script provides a method to determine this by revolving a region around a specified line.
πŸ’‘Curves
In the script, 'curves' refers to the mathematical functions that define the boundaries of the region being rotated. Specifically, the curves mentioned are y equals 0, x equals 4, and y equals the square root of x. These curves are essential in defining the shape of the region whose volume is to be calculated.
πŸ’‘Shell Method
The 'Shell Method' is a technique used to calculate the volume of a solid of revolution. It involves summing the volumes of cylindrical shells that are formed by rotating thin slices of the region around the axis of revolution. The professor prefers this method for the given problem as it simplifies the calculation by not requiring the subtraction of any missing pieces.
πŸ’‘Radius
The 'radius' in the context of the shell method is the distance from the axis of rotation to the outer edge of the shell. In the script, the professor explains that the radius is determined by the difference in x-values between the line of rotation (x=6) and the curve at any given x, which is represented as 6 - x.
πŸ’‘Height
In the shell method, 'height' is the vertical distance from the axis of rotation to the top of the shell. For the given problem, the height is determined by the function y, which is the square root of x. This height is crucial for calculating the volume of each shell in the integral.
πŸ’‘Integral
An 'integral' in calculus is a mathematical concept that represents the area under a curve between two points. In the video, the professor uses integration to calculate the volume of the solid by summing up the volumes of infinitesimally small shells, which is represented by the integral of 2*pi*r*h with respect to x.
πŸ’‘Two-Dimensional Region
A 'two-dimensional region' is the area enclosed by the curves on a plane. In the script, the professor instructs to sketch this region to understand the shape and boundaries that will be revolved around the axis to form the solid. This region is bounded by y=0, x=4, and y=√x.
πŸ’‘Three-Dimensional Picture
A 'three-dimensional picture' refers to a mental or visual representation of the solid object in 3D space. The professor mentions that while a precise 3D visualization is not necessary, having a basic understanding of the 2D region and its rotation around the line x=6 helps in conceptualizing the problem.
πŸ’‘Gap
In the script, a 'gap' refers to the space between the region being rotated and the axis of rotation. The professor notes that there is a gap because the region is not connected to the line x=6, which is an important observation for understanding the geometry of the problem and choosing the appropriate method for calculating the volume.
πŸ’‘Rotation Line
The 'rotation line' is the axis around which the two-dimensional region is rotated to form the solid of revolution. In the video, the rotation line is specified as x equals 6, and understanding its position relative to the region is essential for setting up the problem correctly.
Highlights

Introduction to the problem of finding the volume of a solid generated by rotating a region bounded by certain curves around the line x=6.

Emphasis on sketching the two-dimensional region and understanding the rotation line's position relative to it.

Explanation of the curves defining the region: y=0, x=4, and y=√x.

Introduction of the shell method for solving the problem, an alternative to the washer method.

Illustration of the region and the rotation line with a rough sketch to visualize the problem.

Identification of the gap in the region and its implications for the chosen method.

Decision to use the shell method due to its simplicity in handling the gap without needing to subtract pieces.

Discussion on choosing the variable for integration, whether x or y, based on the orientation of the shells.

Identification of the height (h) of the shells as the function y=√x.

Calculation of the radius (r) as the distance from the rotation line x=6 to the curve, resulting in r=6-x.

Setup of the integral for the volume using the formula 2*pi*r*h with the identified radius and height functions.

Simplification of the integral by expressing the square root of x as x^(1/2).

Application of the power rule for integration to find the volume of the solid.

Reiteration of the importance of choosing the simplest method for the problem, in this case, the shell method.

Final note on the uniqueness of the problem due to the non-standard axis of rotation and the disconnected region.

Summary of the steps taken to solve the problem, emphasizing the process over the final numerical answer.

Transcripts

Browse More Related Video

Volume of a Paraboloid via Disks | MIT 18.01SC Single Variable Calculus, Fall 2010

Shell Method - Volume of Revolution

2010 AP Calculus AB Free Response #4

2019 AP Calculus AB Free Response Question #5

2014 AP Calculus AB Free Response #2

Volume of Revolution Examples - Vertical Axis

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Solid of RevolutionMath TutorialVolume CalculationShell MethodIntegral CalculusEducational ContentGeometry Problems3D RotationMathematical ConceptsProblem Solving