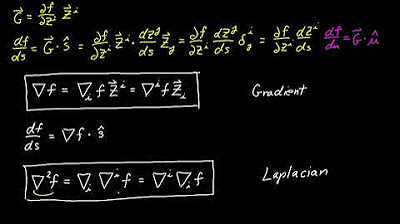Divergence notation
TLDRThis educational video script explains the concept of divergence in vector fields, focusing on two and three dimensions. It introduces the divergence as the scalar sum of partial derivatives of the vector field's components. The script uses the nabla symbol as a mnemonic device, illustrating the dot product between the nabla operator and the vector function. It also extends the concept to higher dimensions, emphasizing the nabla's adaptability and the simplicity of the divergence formula, which remains consistent across various dimensions.
Takeaways
- 📚 The divergence of a two-dimensional vector field with component functions P and Q is defined as the sum of the partial derivative of P with respect to x and the partial derivative of Q with respect to y.
- 📝 Another notation for divergence uses the nabla symbol (∇), which represents a vector of partial differential operators, and is thought of as taking the dot product with the vector-valued function.
- 🔍 The mnemonic for divergence involves imagining the nabla as a vector with components ∂/∂x and ∂/∂y, which take the partial derivatives of the respective components of the vector field.
- 📐 In the context of divergence, the multiplication of the nabla operator with a component of the vector field is interpreted as taking the partial derivative of that component.
- 📈 The divergence formula can be extended to higher dimensions, such as a three-dimensional vector field with components P, Q, and R, each being functions of x, y, and z.
- 📊 The three-dimensional divergence involves taking the dot product of the nabla operator with three components (∂/∂x, ∂/∂y, ∂/∂z) and the corresponding components of the vector field.
- 🧠 The concept of divergence can be generalized to higher dimensions beyond three, following the same pattern of taking partial derivatives with respect to each dimension.
- 🌐 The nabla notation is advantageous as it provides a compact and scalable way to express the divergence formula, which remains consistent across different dimensions.
- 🔑 The mnemonic device of the nabla as a vector of partial differential operators helps in visualizing and remembering the formula for divergence in various dimensions.
- 📚 The script emphasizes the importance of understanding the symbolic representation and the process of taking partial derivatives as part of the divergence calculation.
- 🔄 The script concludes by highlighting the scalability of the divergence concept, applicable to any number of dimensions, showcasing the power of mathematical notation.
Q & A
What is a two-dimensional vector field?
-A two-dimensional vector field is a mathematical concept where each point in a plane is associated with a vector. It is defined by two component functions, typically denoted as P(x, y) and Q(x, y), which represent the vector's components in the x and y directions, respectively.
What is the divergence of a vector field?
-The divergence of a vector field is a scalar-valued function that measures the magnitude of a vector field's source or sink at a given point. It is defined as the sum of the partial derivatives of the vector field's components with respect to each spatial coordinate.
What is the alternative notation for divergence using the nabla symbol?
-The alternative notation for divergence uses the nabla symbol, an upside-down triangle (∇), and represents it as the dot product between the nabla operator and the vector-valued function. This mnemonic helps in remembering the formula for divergence.
What does the nabla operator consist of in the context of divergence?
-In the context of divergence, the nabla operator consists of partial differential operators. For a two-dimensional vector field, it is thought of as a vector with components representing the partial derivatives with respect to x and y.
How is the dot product between the nabla operator and a vector-valued function visualized?
-The dot product is visualized by lining up terms and multiplying corresponding components. For instance, the first component of the nabla operator (∂/∂x) is multiplied by the P component of the vector field, and the second component (∂/∂y) is multiplied by the Q component.
What does the divergence formula look like for a two-dimensional vector field?
-The divergence formula for a two-dimensional vector field is given by ∇ · v = (∂P/∂x) + (∂Q/∂y), where P and Q are the components of the vector field in the x and y directions, respectively.
Can the concept of divergence be extended to higher-dimensional spaces?
-Yes, the concept of divergence can be extended to higher-dimensional spaces. For a three-dimensional vector field with components P, Q, and R, the divergence is given by ∇ · v = (∂P/∂x) + (∂Q/∂y) + (∂R/∂z).
How does the nabla operator change when considering a three-dimensional vector field?
-In a three-dimensional vector field, the nabla operator has three components: ∂/∂x, ∂/∂y, and ∂/∂z. These components represent the partial derivatives with respect to x, y, and z, respectively.
What is the significance of the ordering of variables in the nabla operator?
-The ordering of variables in the nabla operator corresponds to the order in which they appear in the function's arguments. This is important for correctly applying the partial derivative operators when calculating the divergence.
Why is the nabla notation considered useful for describing divergence in higher dimensions?
-The nabla notation is useful for describing divergence in higher dimensions because it provides a compact and consistent way to express the formula for divergence, regardless of the number of dimensions involved.
How does the script suggest thinking about the changes to the z component of a vector field?
-The script suggests thinking about the changes to the z component of a vector field in terms of how the value of z changes as one moves up and down in the z direction, affecting the vector field's divergence.
Outlines
📚 Introduction to Divergence in Vector Fields
This paragraph introduces the concept of divergence in a two-dimensional vector field, defined by the component functions P and Q. It explains the divergence as the sum of the partial derivatives of P with respect to x and Q with respect to y. The paragraph also introduces an alternative notation for divergence using the nabla symbol, suggesting a mnemonic of taking the dot product between the nabla and the vector function. This mnemonic helps in remembering the formula and understanding the process of evaluating the divergence, which can also be extended to higher-dimensional vector fields.
Mindmap
Keywords
💡Vector Field
💡Component Functions
💡Divergence
💡Partial Derivative
💡Nabla Symbol
💡Dot Product
💡Gradient
💡Scalar-Valued Function
💡Higher-Dimensional Functions
💡Mnemonic Device
Highlights
The divergence of a two-dimensional vector field with component functions P and Q is defined as the sum of the partial derivatives of P with respect to x and Q with respect to y.
An alternative notation for divergence uses the nabla symbol, which represents taking the dot product with a vector full of partial differential operators.
The mnemonic for the nabla symbol is to think of it as a vector with components that take the partial derivatives of a function.
The dot product between the nabla symbol and a vector-valued function results in the same formula for divergence as the partial derivatives.
The divergence concept can be extended to higher-dimensional functions, such as three-dimensional vector fields.
In a three-dimensional vector field with components P, Q, and R, the divergence is calculated using the nabla symbol with three components: partial derivatives with respect to x, y, and z.
The order of variables in the nabla symbol should match the order they appear in the function.
The divergence formula for a three-dimensional vector field involves evaluating the partial derivatives at the respective components P, Q, and R.
The concept of divergence can be generalized to even higher dimensions beyond three, following the same pattern of taking partial derivatives with respect to each variable.
The nabla notation provides a compact and elegant way to describe the divergence formula, which would otherwise become cumbersome to write in higher dimensions.
The mnemonic device of the nabla symbol as a vector of partial differential operators helps in remembering the formula for divergence.
The dot product between the nabla symbol and a vector-valued function is a key step in calculating the divergence.
The partial derivative operators in the nabla symbol are evaluated at the components of the vector-valued function to calculate divergence.
The divergence formula remains consistent across different dimensions, following a simple pattern that can be easily generalized.
The nabla notation encapsulates the concept of divergence in a way that is easy to visualize and understand, even in higher dimensions.
The transcript provides a clear explanation of the divergence of vector fields in both two and three dimensions, using the nabla symbol as a mnemonic device.
The concept of divergence is fundamental in understanding how vector fields change with respect to their input variables in different dimensions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: