Calculus AB Homework 3.1 Derivative Rules

Michelle Krummel
29 Oct 201728:53
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial guides viewers through solving calculus problems involving differentiation and tangent lines. It covers finding derivatives of composite functions, analyzing increasing/decreasing behavior, and determining horizontal tangents. The script also addresses piecewise functions' non-differentiability and provides a method to find the equation of a tangent line at a given point. The video concludes with solving for the values of 'k' where a linear function is tangent to a quadratic function.

Takeaways
  • 📚 The video covers the solution to Unit 3 homework problems 1 through 7, focusing on differentiable functions and their applications.
  • 🔍 The script introduces a new function H(x) defined as 3f(x) - 4G(x), and calculates its value and derivative at x = 2 using given values of f(2), G(2), f'(2), and G'(2).
  • 📈 It explains how to find the equation of a tangent line to a function at a given point, using the point of tangency and the slope derived from the function's derivative.
  • 📝 The script discusses determining whether a function is increasing or decreasing at a specific point by evaluating the sign of its derivative at that point.
  • 🤔 It poses a question about the local linearization of a function P(x) to estimate its value at a nearby point, showcasing the application of tangent lines in approximation.
  • 📉 The video explores piecewise linear functions and identifies the points where they are not differentiable, highlighting the concept of corner points and non-existent limits of derivatives.
  • 🧩 In a separate problem, the script combines two functions to form a new function R(x) and identifies the points where R(x) is not differentiable, demonstrating the propagation of non-differentiability.
  • 📐 The script calculates the derivative of a function involving a rational exponent, simplifying the expression to a more familiar radical form.
  • ✏️ It simplifies and differentiates a cubic polynomial function, showing the process of applying the power rule to each term of the polynomial.
  • 📉 The video finds the equation of a tangent line to a function involving a cube root, using the point of tangency and the slope from the derivative.
  • 🔑 The script concludes by solving for the values of K that make a linear function tangent to a quadratic function, emphasizing the condition of equal slopes at the point of tangency.
Q & A

  • What is the definition of function H(x) in the script?

    -Function H(x) is defined as H(x) = 3 * f(x) - 4 * G(x), where f(x) and G(x) are differentiable functions.

  • What are the values of f(2) and G(2) as given in the script?

    -The values are f(2) = 5 and G(2) = -3.

  • What is the derivative of function H(x), denoted as H'(x), in terms of f(x) and G(x)?

    -H'(x) is expressed as 3 * f'(x) - 4 * G'(x), where f'(x) and G'(x) are the derivatives of f(x) and G(x) respectively.

  • What is the value of H'(2) calculated in the script?

    -The value of H'(2) is calculated to be -19/2.

  • How is the equation of the tangent line to y = H(x) at the point (2, H(2)) derived?

    -The equation of the tangent line is derived using the point-slope form, Y - 27 = (-19/2) * (X - 2), with the point of tangency being (2, 27) and the slope being H'(2) = -19/2.

  • What does the derivative of function P(x) at x = 2 indicate about the function at that point?

    -The derivative P'(2) being positive indicates that the function P(x) is increasing at x = 2.

  • What is the function V(t) in the script and is it increasing or decreasing at t = 1/2?

    -Function V(t) is defined as V(t) = e^t + arccos(t). It is decreasing at t = 1/2 as indicated by the negative derivative V'(1/2).

  • What are the values of x where the piecewise linear functions P and Q are not differentiable?

    -The functions P and Q are not differentiable at x = -1 and x = 1, which are the corner points of their respective graphs.

  • How is the function R(x) defined in terms of P(x) and Q(x) in the script?

    -Function R(x) is defined as R(x) = P(x) + 2 * Q(x), which is a combination of the functions P and Q scaled by a factor of 2.

  • What is the slope of the tangent line to the graph of G(x) = 2 / (x^(1/4)) at x = 1?

    -The slope of the tangent line at x = 1 is -1/2, which is the value of G'(1).

  • What are the values of K for which the line y = 5x - 16 is tangent to the graph of f(x) = x^2 - kx?

    -The values of K for which the line is tangent to the graph are K = 3 and K = -13, derived from solving the system of equations for tangency.

Outlines
00:00
📚 Calculus Homework Solutions

This paragraph covers the solution to a calculus homework problem set. The focus is on differentiable functions F and G with given values and derivatives at x=2. A new function H(x) is defined and the task is to find H(2) and its derivative at that point. The process involves direct substitution and application of the derivative rules for composite functions. The solution to H(2) is 27, and H'(2) is calculated to be -19/2. The paragraph also discusses finding the equation of the tangent line to H(x) at x=2, using the point-slope form of a line equation. Part B continues with the analysis of the function P(x) to determine its increasing or decreasing nature at x=2, concluding that P is increasing at that point. The final part of the paragraph involves local linearization to estimate P(2.3), resulting in an approximate value of -10.9.

05:00
🔍 Advanced Calculus Problem Exploration

The second paragraph delves into more complex calculus problems involving functions W(t), V(t), and piecewise linear functions P(x) and Q(x). The task for W(t) is to find its derivative using the given derivatives of R(t) and S(t), resulting in a derivative expression involving powers and logarithms. For V(t), the paragraph explores whether the function is increasing or decreasing at t=1/2 by evaluating its derivative at that point, concluding that V is decreasing. The piecewise functions P and Q are analyzed for points of non-differentiability, identifying the corners at x=±1. The paragraph concludes with the construction of a new function R(x) as a combination of P and Q, and the analysis of its points of non-differentiability and derivative values at specific points.

10:01
📉 Tangent Line Equations and Derivatives

This paragraph discusses the process of finding tangent line equations and derivatives for various functions. It starts with simplifying and differentiating a function involving a rational exponent, resulting in a derivative with a negative exponent, which is then rewritten in radical form. The paragraph continues with finding the derivative of a polynomial function and simplifying it to a more understandable form. The next function involves a complex rational expression, which is simplified before differentiation. The process includes combining like terms and applying the power rule to find the derivative. The final part of the paragraph focuses on finding the equation of a tangent line to a function at a specific point, including calculating the function value and its derivative at that point to use in the point-slope form of the line equation.

15:06
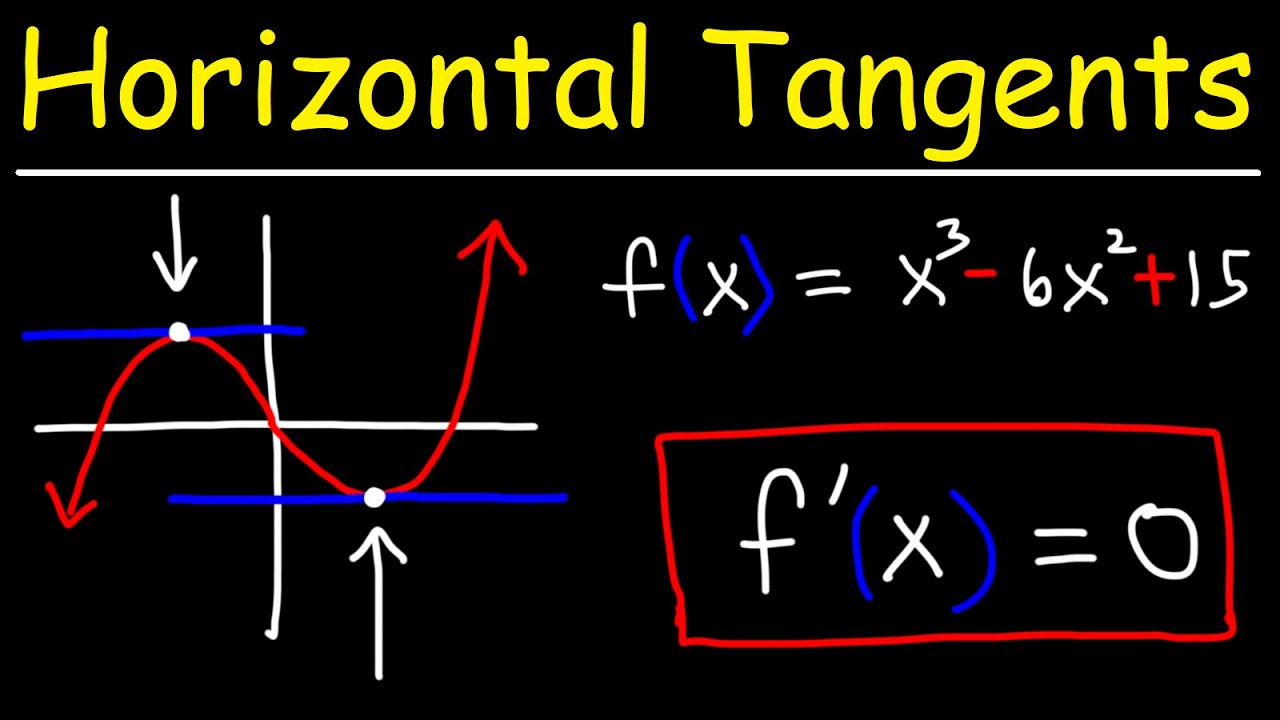
🔢 Solving for Horizontal Tangents and Tangent Intersections

The final paragraph addresses two calculus problems involving the concept of horizontal tangents and tangent intersections. The first problem involves finding the values of x for which a given function has a horizontal tangent, which is achieved by setting the derivative equal to zero and solving for x, yielding solutions of x=0, ±2. The second problem seeks the values of K for which a linear function is tangent to a quadratic function. This is done by setting the equations equal to each other and solving for the point of tangency, followed by equating and solving for the slopes, resulting in K values of 3 and -13.

Mindmap
Keywords
💡Differentiable functions
Differentiable functions are a class of functions that have derivatives at every point in their domain. In the context of the video, the functions F and G are stated to be differentiable, implying that their rates of change (slopes of the tangent lines) can be calculated at any point. This concept is central to the video's theme of calculus, particularly in finding derivatives and analyzing the behavior of functions.
💡Derivative
The derivative of a function measures the rate at which the function value changes with respect to changes in its input. In the video, derivatives are calculated for various functions to determine the slope of tangent lines and to analyze the increasing or decreasing nature of the functions. For example, 'F prime of 2' and 'G prime of 2' are used to find the slopes of the tangent lines to the functions F and G at the point x=2.
💡Tangent line
A tangent line is a straight line that touches a curve at a single point without crossing it. In the video, the script discusses finding the equations of tangent lines to various functions at specific points. The slope of the tangent line is given by the derivative of the function at that point, and the point of tangency is used to write the equation in point-slope form.
💡Increasing function
An increasing function is one where the function values increase as the input values increase. In the video, the script determines whether the function P is increasing at a specific point by examining the sign of its derivative at that point. A positive derivative indicates that the function is increasing, as seen when 'P prime of 2' is found to be positive.
💡Decreasing function
A decreasing function is the opposite of an increasing function; its values decrease as the input values increase. The script uses the derivative to determine if a function is decreasing, as in the case of function V, where 'V prime of 1/2' is negative, indicating that V is decreasing at that point.
💡Piecewise linear functions
Piecewise linear functions are composed of multiple linear segments, each defined by a different linear equation. In the video, the functions P and Q are described as piecewise linear, and the script identifies points where these functions are not differentiable, specifically at the corners where the segments meet, such as at x = -1 and x = 1.
💡Power rule
The power rule is a fundamental principle in calculus for finding the derivative of a function that is raised to a power. It states that the derivative of x^n (where n is a constant) is nx^(n-1). The video uses the power rule multiple times to find derivatives of functions, such as 'H of x' and 'f of x'.
💡Rational exponent
A rational exponent is an exponent that is a fraction rather than a whole number. In the video, the script rewrites expressions using rational exponents to simplify the process of differentiation. For example, 'H of x' is rewritten using a rational exponent, allowing for the application of the power rule to find its derivative.
💡Horizontal tangent
A horizontal tangent to a curve is a tangent line with a slope of zero, meaning the function has a constant rate of change at that point. The video script discusses finding the values of x for which the function 'f of x' has a horizontal tangent by setting the derivative equal to zero and solving for x, resulting in x = -2, 0, and 2.
💡Point of tangency
The point of tangency is the exact point on the curve where the tangent line touches the curve. In the video, the script calculates the point of tangency for various functions by substituting the x-value into the function to find the corresponding y-value. This point is then used to write the equation of the tangent line.
💡Slope
Slope is a measure of the steepness of a line, and in calculus, it is often represented by the derivative of a function. The video script frequently refers to the slope in the context of tangent lines, such as 'the slope of our tangent line is H prime of 2', and uses it to determine the equation of the tangent line.
Highlights

Introduction of a method to work through unit 3 homework problems 1 through 7.

Definition of a new function H(x) as a combination of differentiable functions f(x) and g(x).

Calculation of H(2) using given values of f(2) and g(2).

Derivation of H'(x) using the derivative rules for f(x) and g(x).

Determination of H'(2) by substituting the known derivatives of f and g at x=2.

Finding the equation of the tangent line to y=H(x) at the point (2, H(2)).

Analysis of the function P(x) to determine if it is increasing, decreasing, or neither at x=a.

Calculation of P'(2) to understand the behavior of P(x) at x=2.

Derivation of the local linearization equation for P(x) at x=2.

Estimation of P(2.3) using the local linearization method.

Introduction of functions R(t) and S(t) with given derivatives and restricted domain.

Derivation of W'(t) for the function W(t) which is a combination of R(t) and S(t).

Finding the equation of the tangent line to y=W(t) at the point (1/2, W(1/2)).

Analysis of the function V(t) to determine if it is increasing or decreasing at t=1/2.

Calculation of V'(1/2) to understand the behavior of V(t) at t=1/2.

Identification of points where piecewise linear functions P and Q are not differentiable.

Determination of points where the combined function R(x) is not differentiable.

Calculation of R'(-2) and R'(0) for the function R(x).

Derivation of the tangent line equation to y=R(x) at the point (2, R(2)).

Rewriting of functions using rational exponents and finding their derivatives.

Simplification of derivatives for functions involving piecewise definitions or complex expressions.

Finding the equation of the tangent line to the graph of G(x) at x=1.

Determination of values of x for which the function f(x) has a horizontal tangent.

Solving for the values of K where the line y=5x-16 is tangent to the graph of f(x)=x^2-Kx.

Transcripts

Browse More Related Video

Calculus AB Homework 3.3 The Quotient Rule

Calculus AB Homework 3.1 The Sine and Cosine Functions

Calculus AB Homework 3.4 The Chain Rule

Calculus AB Homework 4.1: Implicit Differentiation

Calculus AB Homework 2.1 The Derivative

How to Find The Point Where The Graph has a Horizontal Tangent Lines Using Derivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus ProblemsDerivative TutorialFunction AnalysisTangent LineDifferentiabilityPiecewise FunctionsSlope CalculationRational ExponentsPower RuleTrigonometric FunctionsLinear Approximation