1 | MCQ | Practice Sessions | AP Calculus AB

Advanced Placement
17 Apr 202318:05
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging video transcript, educators Virge Cornelius and Mark Kiraly guide viewers through a series of calculus problems as part of an AP Daily Practice session. They emphasize the importance of mastering various differentiation rules, including the product rule, quotient rule, and chain rule, which are essential for solving the problems presented. The session is designed to be concise, allowing students to practice multiple-choice questions efficiently. The educators also discuss the significance of knowing when to apply each rule and the value of creating a formula sheet or flashcards for quick reference. They provide insights into solving problems quickly and effectively, encouraging students to keep their pencils moving and not to dwell too long on a single question. The session concludes with a reminder of the importance of understanding the questions and knowing the differentiation rules to succeed in the AP exam.

Takeaways
  • 📚 **Product Rule**: When differentiating a product of two functions, use the product rule: (first function * derivative of second function) + (second function * derivative of first function).
  • 🔢 **Quotient Rule**: For a quotient of two functions, the derivative is found by: (denominator * derivative of numerator) - (numerator * derivative of denominator), all divided by the square of the denominator.
  • 🔽 **Implicit Differentiation**: When you can't explicitly solve for y, use implicit differentiation to find dy/dx by differentiating each term with respect to x.
  • ⏱️ **Time Management**: For non-calculator multiple-choice questions, aim to spend about 2 minutes per question to manage time effectively during the exam.
  • 📉 **Derivatives of Trigonometric Functions**: Remember that the derivative of tangent is secant squared, and for cofunctions, the derivatives are negative.
  • 📈 **Chain Rule**: When differentiating composite functions, use the chain rule, which involves differentiating the outer function and multiplying by the derivative of the inner function.
  • 📋 **Build a Formula Sheet**: Create a formula sheet or flashcards to have a quick reference for all the differentiation rules you need to know.
  • 🧮 **Practice Efficiency**: Practice solving problems efficiently to recognize when you can stop partway through a calculation if you can identify the answer from the options.
  • 📘 **Review Exponential Functions**: Know the derivative of exponential functions, especially when the base is not 'e', as it involves multiplying by the natural log of the base.
  • 🔁 **Cofunctions and Derivatives**: Be aware that the derivatives of cofunctions (like cotangent) are negative, contrasting with non-cofunctions.
  • ✅ **Multiple Choice Strategy**: On a multiple-choice exam, after practicing enough, you can often determine the correct answer without completing every step, saving time for more challenging questions.
  • 📝 **Stay Organized**: Keep your work neat and organized, especially when dealing with complex derivatives, to avoid confusion and calculation errors.
Q & A

  • What is the name of the educational program that Virge Cornelius and Mark Kiraly are discussing?

    -The educational program they are discussing is called 'AP Daily Practice'.

  • What type of problems are the teachers focusing on during this session?

    -The teachers are focusing on multiple-choice problems that do not require the use of a calculator.

  • What is the significance of the link mentioned in the transcript?

    -The link is provided so that students can print out the problems discussed in the session for personal practice.

  • What rule of calculus is used when dealing with a product of two functions?

    -The Product Rule is used when dealing with a product of two functions in calculus.

  • What is the derivative of the tangent function with respect to x?

    -The derivative of the tangent function with respect to x is secant squared x.

  • What is the key difference in the derivative of cofunctions compared to regular functions?

    -The derivative of cofunctions is negative, whereas the derivative of regular functions is positive.

  • What rule is applied when finding the derivative of a quotient of two functions?

    -The Quotient Rule is applied when finding the derivative of a quotient of two functions.

  • What is the derivative of the natural logarithm function with respect to x?

    -The derivative of the natural logarithm function with respect to x is 1/x.

  • What is the process called when differentiating an equation that is not explicitly solved for y?

    -The process is called Implicit Differentiation.

  • What rule is applied when finding the derivative of a composite function?

    -The Chain Rule is applied when finding the derivative of a composite function.

  • What is the derivative of an exponential function with base 'a' raised to the power of x?

    -The derivative is 'a' raised to the power of x multiplied by the natural log of 'a'.

  • What is the general advice given by the teachers for approaching multiple-choice calculus problems?

    -The teachers advise knowing the differentiation rules well, building a formula sheet or flashcards, and not spending too much time on a single problem. They also suggest that understanding what is being asked in a problem is key to knowing how to solve it.

Outlines
00:00
📚 Introduction to AP Daily Practice

The video begins with Virge Cornelius and Mark Kiraly introducing their AP Daily Practice session. They explain that the videos will be short, allowing students to get a lot of practice in a short amount of time. The focus of this session is on multiple-choice questions that do not require a calculator. They provide a link for students to print out the new problems they've created for the 8 sessions. The first problem involves finding the derivative of y = x^2 * tan(x), which leads into a discussion about the product rule in calculus.

05:01
🧮 Applying the Quotient Rule and Implicit Differentiation

The second paragraph covers the application of the quotient rule and implicit differentiation. Virge and Mark work through a problem involving the derivative of f(x) = ln(x) / sqrt(x) and then move on to a problem that requires implicit differentiation where the equation involves x and y: x^4 - 3x*cos(y) = 10. They discuss the importance of knowing differentiation rules and when to apply them, such as the power rule, product rule, and chain rule.

10:04
⏱️ Time Management and Efficiency in Problem Solving

In the third paragraph, the educators emphasize the importance of time management during the AP exam, noting that students have two minutes per question. They suggest that with enough practice, students can often identify the correct answer before fully completing a problem, allowing them to spend more time on more challenging questions. They also highlight the need to maintain concentration and not get distracted by constants in the equations.

15:05
📈 Derivatives of Exponential Functions and Review

The final paragraph focuses on the derivatives of exponential functions and the use of the chain rule. They work through a problem involving the derivative of 5^(x^2) evaluated at x = 3. Virge and Mark review the chain rule and its application to composite functions, and they also discuss the derivative of e^x, highlighting the unique property that the derivative of this function is the function itself. They conclude with advice for students to continue practicing and reviewing their calculus rules and to keep their pencils moving during the exam.

Mindmap
Keywords
💡AP Daily Practice
AP Daily Practice refers to a series of short video sessions designed to help students prepare for the AP (Advanced Placement) exams. In the context of the video, it is the name of the educational program that the speakers, Virge Cornelius and Mark Kiraly, are introducing and discussing. The aim is to provide a focused and efficient way for students to practice AP exam questions within a limited time frame.
💡Product Rule
The Product Rule is a fundamental theorem in calculus for differentiating products of two functions. Defined as the derivative of a product being the first function times the derivative of the second plus the second function times the derivative of the first, it is essential for solving problems involving multiplication of functions. In the video, the Product Rule is used to find the derivative of y = x^2 * tan(x), illustrating its application in solving AP exam questions.
💡Quotient Rule
The Quotient Rule is a calculus theorem used to find the derivative of a quotient of two functions. It states that the derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. The Quotient Rule is highlighted in the video when the speakers differentiate f(x) = ln(x) / sqrt(x), demonstrating its importance in AP calculus problems.
💡Implicit Differentiation
Implicit Differentiation is a method used in calculus to find the derivative of an equation that is not explicitly solved for one of the variables, typically y or x. It involves differentiating both sides of an equation with respect to the variable you are trying to solve for. In the video, implicit differentiation is used to find dy/dx for the equation x^4 - 3x*cos(y) = 10, showcasing its role in handling complex, non-separable equations.
💡Chain Rule
The Chain Rule is a mathematical theorem that allows the computation of the derivative of a composite function. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, times the derivative of the inner function. The Chain Rule is mentioned in the context of differentiating an exponential function to the power of x squared, highlighting its use in multi-layered functions.
💡Derivative
A Derivative in calculus represents the rate at which a function is changing at a certain point. It is a fundamental concept used to analyze the behavior of functions and is often calculated using various rules such as the Product Rule, Quotient Rule, and Chain Rule. Throughout the video, the concept of derivatives is central to solving the multiple-choice questions presented, with examples including the derivatives of x^2*tan(x), ln(x)/sqrt(x), and others.
💡Cofunctions
Cofunctions are trigonometric functions that are related such that the sine of an angle is equal to the cosine of its complement, and similarly for the other trigonometric functions. The concept of cofunctions is mentioned in the context of their derivatives, where the derivative of a cofunction is the negative of the derivative of the original function, as seen when discussing the derivative of tangent versus cotangent.
💡Multiple Choice Questions
Multiple Choice Questions are a type of question format where respondents are given a question and a set of possible answers from which they must choose the correct one. In the video, multiple-choice questions are the focus of the AP Daily Practice session, with the speakers working through various calculus problems that are typical of those found on AP exams.
💡Exponential Function
An Exponential Function is a mathematical function of the form f(x) = a^x, where 'a' is a positive real number not equal to 1. Exponential functions are important in various fields due to their properties of rapid growth or decay. In the video, the speakers differentiate an exponential function, emphasizing the need to understand the unique behavior of such functions when applying the Chain Rule.
💡Natural Logarithm
The Natural Logarithm, often denoted as ln(x), is the logarithm of a number to the base e (approximately 2.71828). It is widely used in mathematics, particularly in calculus, and is part of the derivative of exponential functions. In the video, the natural logarithm is used in the differentiation of the function f(x) = ln(x)/root(x), demonstrating its role in calculus problems.
💡Differentiation Rules
Differentiation Rules are mathematical theorems and formulas used to find derivatives of functions. These include the Power Rule, Product Rule, Quotient Rule, Chain Rule, and others. The video emphasizes the importance of knowing these rules for solving calculus problems, particularly in the context of preparing for AP exams where various differentiation rules are applied to a range of problems.
Highlights

Introduction of AP Daily Practice sessions with short videos for efficient practice.

Focus on multiple-choice questions without the use of a calculator.

Availability of new problems for practice, written by the session's instructors.

Explanation of the product rule in calculus for derivatives.

Derivation of y = x^2 * tan(x) using the product rule.

Differentiation between cofunctions and their derivatives' signs.

Application of the quotient rule to find the derivative of a function.

Use of the power rule for derivatives, specifically for x^(1/2).

Substitution of values into derivatives to solve for a specific point.

Implicit differentiation for functions not explicitly defined in terms of x.

Technique to avoid losing concentration when differentiating constants.

Strategies for time management during non-calculator multiple-choice questions.

Importance of understanding what is being asked in a problem to know which rule to apply.

Review of the chain rule for composite functions.

Derivation of exponential functions and the role of the natural logarithm.

Evaluation of derivatives at specific points using substitution.

Advice on building a formula sheet or flashcards for differentiation rules.

Emphasis on the necessity of knowing differentiation rules for problem-solving.

Encouragement to keep working through problems and not to dwell on a single question for too long.

Transcripts

Browse More Related Video

8 | FRQ (No Calculator) | Practice Sessions | AP Calculus AB

2022 Live Review 1 | AP Calculus AB | Practicing with Derivatives & Chain Rule

2021 Live Review 1 | AP Calculus AB | Understanding Derivatives & Chain Rule

2022 Live Review 4 | AP Calculus AB | Integrals & Using the Fundamental Theorem of Calculus

2022 Live Review 3 | AP Calculus AB | How to Find Limits & Continuity

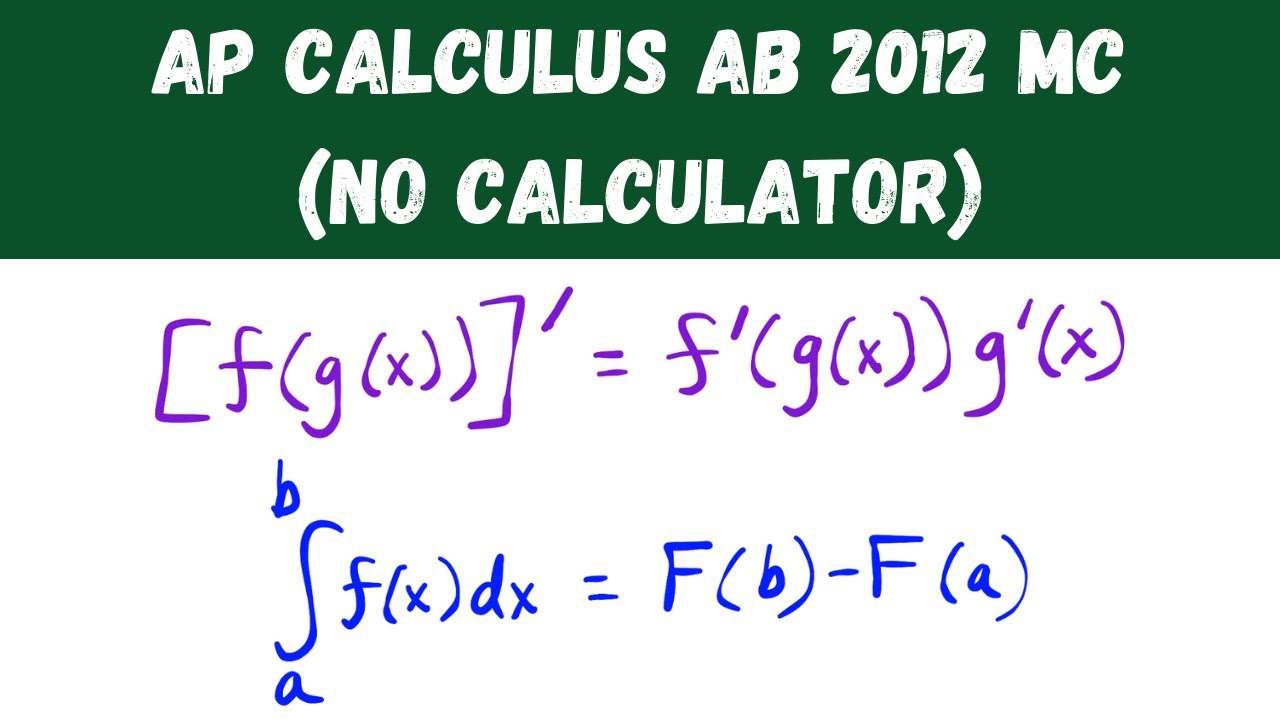
AP Calculus AB 2012 Multiple Choice (no calculator) - Questions 1-28

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusDaily PracticeDifferentiation RulesProduct RuleQuotient RuleImplicit DifferentiationChain RuleStudy StrategiesExam PreparationEducational ContentMathematics TutorialHigh SchoolOnline Learning