The Math Major
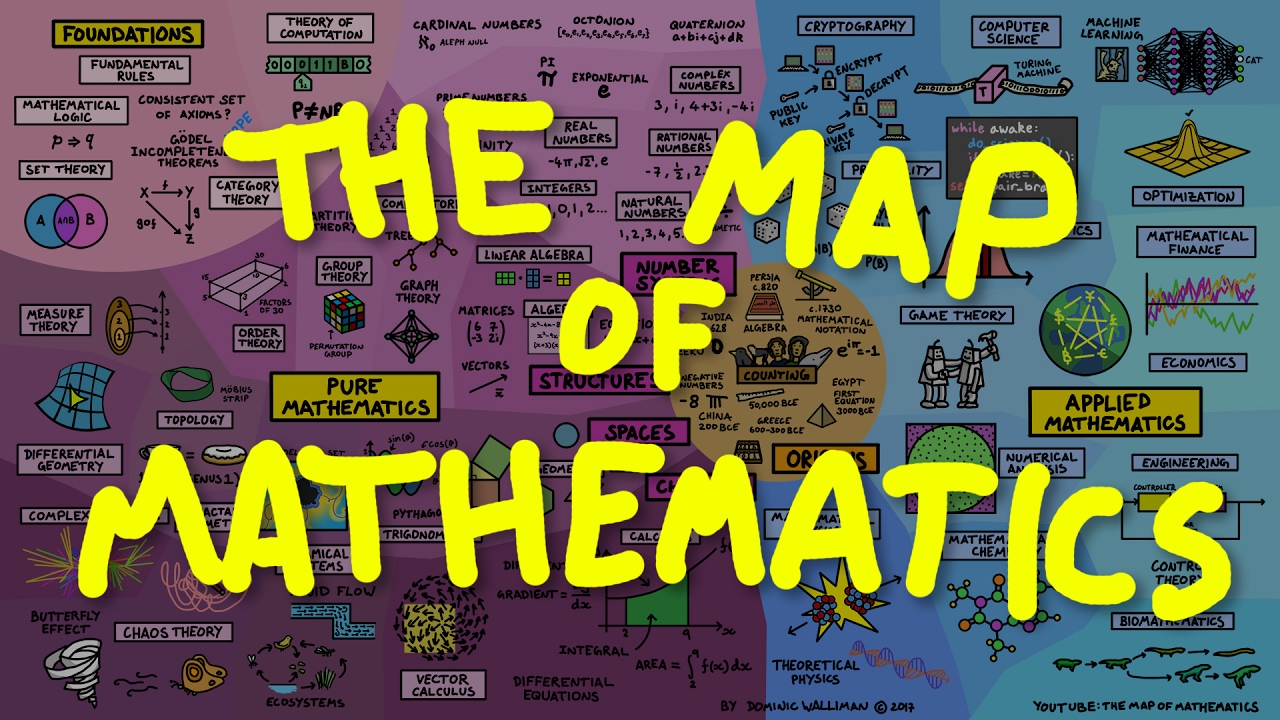
TLDRThe video script delves into the world of mathematics, distinguishing between applied and pure math. It outlines the various paths a math major can take, including the classes they might expect and the diverse careers available beyond teaching. The script highlights how applied math is used to solve real-world problems across different fields, while pure math focuses on mathematical concepts and proofs. It also touches on the historical significance of pure math, such as prime numbers' role in modern encryption systems, and the practical applications that emerge over time.
Takeaways
- 📚 Math can be divided into two main subfields: applied math and pure math.
- 🔍 Applied math uses mathematical concepts to solve real-world problems in fields like physics, chemistry, biology, computer science, engineering, finance, etc.
- 🌟 Pure math focuses on solving problems within the realm of mathematics itself, often leading to theoretical advancements with potential future applications.
- 📈 Applied math students typically study calculus, including differential and integral calculus, vector analysis, differential equations, and numerical analysis.
- 🔧 Engineering and physics majors often take the same applied math classes, but applied mathematicians delve deeper into higher-level math concepts.
- 🔍 Pure math involves a significant amount of proofs and logical reasoning, which are different from the proofs encountered in high school geometry.
- 🎓 A math major can expect to take classes on proof techniques, abstract algebra, and other advanced pure math topics.
- 🚀 Practical applications of pure math, such as prime numbers, can have significant real-world uses like securing online transactions through encryption.
- 🌐 Applied math students can work on projects related to modeling natural phenomena, optimizing systems, and predicting outcomes in various fields.
- 📊 Common minors for applied math majors include computer science, physics, statistics, and economics, enhancing their ability to apply math to real-world problems.
- 🎯 Both applied and pure math majors can pursue a wide range of careers, from academia and research to industry and finance.
Q & A
What are the two main subfields of math?
-The two main subfields of math are applied math and pure math.
What is applied math used for?
-Applied math is used to solve problems outside of math, such as in physics, chemistry, biology, computer science, engineering, finance, and more.
Can you provide an example of how pure math is used?
-An example of pure math usage is proving there is an infinite amount of prime numbers or studying higher dimensional spheres and their properties.
How does the study of prime numbers have practical applications?
-The study of prime numbers is used in computer encryption systems to secure information, such as when entering credit card information online.
What are some of the calculus topics covered in a math major?
-In a math major, you will cover topics such as derivatives, integrals, functions of multiple variables, vector analysis, and differential equations.
Why is numerical analysis important in mathematics?
-Numerical analysis is important because it allows for the approximation of solutions to complex problems that cannot be solved exactly, which is useful in real-world applications and computer software for analyzing complex systems.
What is chaos theory and how does it relate to applied math?
-Chaos theory is a branch of applied math that studies systems that are very sensitive to initial conditions, such as the trajectory of a double pendulum which can change dramatically with slight changes in starting position.
What types of real-world problems can applied math be used to solve?
-Applied math can be used to solve real-world problems like modeling the trajectory of oil spills, the spread of viruses, asteroid impacts, optimizing cell phone tower placement, and predicting stock market fluctuations.
What are some common minors for applied math majors?
-Common minors for applied math majors include computer science, physics, statistics, and economics.
What is the main focus of pure math classes?
-The main focus of pure math classes is learning and applying proofs to establish mathematical truths and theorems.
How does a proof by contradiction work?
-A proof by contradiction works by assuming the opposite of what you want to prove, showing that this assumption leads to a contradiction, and thus concluding that the original statement must be true.
Outlines
📚 Introduction to Math Major and its Branches
This paragraph introduces the viewer to the mathematics major, outlining the key areas of study within it. It differentiates between applied and pure mathematics, explaining that applied math focuses on using math to solve real-world problems across various disciplines, while pure math deals with solving problems within the realm of mathematics itself. The paragraph also touches on the versatility of math, highlighting how concepts initially considered theoretical, like prime numbers, can later find practical applications, such as in computer encryption systems.
🔢 In-Depth Look at Applied Mathematics
The second paragraph delves deeper into applied mathematics, detailing the types of classes one might take and the overlap with other majors like physics and engineering. It covers the calculus series, including the study of derivatives and integrals, and extends to vector analysis and differential equations. The importance of numerical analysis is emphasized, explaining how it is used to find approximate solutions to complex problems that cannot be solved exactly. The paragraph also mentions that applied math can be applied to diverse real-world problems, providing examples of senior projects and the interdisciplinary minors that complement a math major.
📝 Understanding Pure Mathematics and Proofs
The final paragraph shifts focus to pure mathematics, emphasizing the importance of proofs in this branch of math. It contrasts the proofs found in high school geometry with those encountered in college-level pure math, encouraging an open mind when approaching these more complex demonstrations. The paragraph introduces the concept of proof by contradiction and provides a brief example of proving that the product of two odd integers is always odd. It also mentions that understanding proofs is crucial for advanced pure math courses, hinting at further topics to be explored in subsequent videos.
Mindmap
Keywords
💡Math Major
💡Applied Math
💡Pure Math
💡Calculus
💡Differential Equations
💡Vector Analysis
💡Numerical Analysis
💡Linear Algebra
💡Chaos Theory
💡Proofs
💡Abstract Algebra
Highlights
Mathematics can be divided into two main subfields: applied math and pure math.
Applied math uses mathematical concepts to solve real-world problems in fields like physics, chemistry, biology, computer science, and engineering.
Pure math focuses on solving problems within mathematics itself, such as proving theorems and exploring abstract concepts.
An example of pure math's practical application is the use of prime numbers in computer encryption systems.
Applied math students take calculus series to learn about derivatives and integrals, which are used to solve problems involving rates of change and areas under curves.
Multivariable calculus is essential for understanding complex systems with functions involving three or more variables, like electromagnetic waves.
Vector analysis is a part of applied math that deals with applying calculus to vector fields, such as magnetic fields or fluid flow.
Differential equations are used to model systems where components change over time or position, and applied math students learn various techniques to solve them.
Partial differential equations are a type of differential equation with more than two variables, used to model systems like heat transfer.
Numerical analysis is the process of finding approximate solutions to math problems when exact solutions are not feasible.
Linear algebra and complex analysis are among the advanced topics studied in applied math.
Applied math students often undertake senior projects that model real-world phenomena, such as oil spills, virus spread, asteroid impacts, and stock market fluctuations.
Common minors for applied math majors include computer science, physics, statistics, and economics.
Pure math involves a significant amount of proofs, which are different from the proofs encountered in high school geometry.
Proof techniques in pure math include direct proof and proof by contradiction, as demonstrated with examples of odd number multiplication and the irrationality of the square root of 2.
Abstract algebra is one of the pure math courses that involves proofs and is covered in a separate video.
The video series continues in part 2, where more applied math classes and pure math courses, as well as their respective careers, will be discussed.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: