Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
TLDRThe video script explores the intriguing patterns formed by plotting prime numbers in polar coordinates, leading to a discussion on the distribution of primes and rational approximations of pi. It explains the formation of spirals and rays in the data visualization, which are linked to residue classes mod 6 and mod 44, and ultimately ties back to Dirichlet's theorem on the distribution of primes across residue classes. The exploration emphasizes the beauty of number theory and the importance of mathematical curiosity-driven learning.
Takeaways
- 📊 Data visualization in polar coordinates can reveal unexpected patterns, even when plotting seemingly random sets like prime numbers.
- 🌀 The spiral patterns observed when plotting prime numbers in polar coordinates are not unique to primes; similar patterns appear with all whole numbers.
- 🔢 The number of spirals (20 for primes, 44 for all numbers) corresponds to the residue classes mod 6 and mod 44, respectively.
- 📈 Residue classes mod 6 and mod 44 are related to the number of radians turned in each step, which is close to full turns for multiples of these numbers.
- 🌌 The 'Milky Way' gaps in the larger spiral pattern occur because certain residue classes mod 44 do not contain any prime numbers.
- 🔍 Prime numbers are distributed relatively evenly across the remaining residue classes that do not share prime factors with 44.
- 🎓 Euler's totient function (phi) counts the number of integers co-prime to a given number, and is used to understand the distribution of primes among residue classes.
- 🏆 Dirichlet's theorem is a fundamental result in number theory that states primes are evenly distributed among residue classes mod n for any number n.
- 🤔 The proof of Dirichlet's theorem is complex and relies on advanced mathematics, including complex analysis.
- 🌟 The exploration of seemingly arbitrary mathematical patterns can lead to profound insights and important theorems, encouraging deeper understanding and appreciation for mathematics.
Q & A
What is the significance of polar coordinates in the context of this script?
-Polar coordinates are used to plot points in 2D space based on their distance from the origin (radius) and the angle they form with the horizontal axis (theta). This visualization method is key to observing the patterns formed by prime numbers when plotted in this coordinate system.
Why are the spirals formed in the polar coordinate plot of prime numbers considered surprising?
-The spirals formed by prime numbers in polar coordinates are surprising because they reveal an unexpected order and pattern within the seemingly chaotic distribution of primes. This visual order contradicts the widely held belief that primes follow no predictable pattern.
What is the role of the number 2π in the formation of spirals in the polar plot?
-The number 2π represents a full circle in radians. The spirals are formed because each step in the polar plot (an increase by one in the angle θ) corresponds to a rotation of approximately one radian (a little less than 1/6 of a full turn). As a result, the points spiral outward as they accumulate around the origin, creating the archimedean spiral pattern.
How does the script relate the distribution of prime numbers to Dirichlet's theorem?
-The script connects the distribution of prime numbers in polar coordinates to Dirichlet's theorem by explaining that the primes are evenly distributed across different residue classes mod n. This theorem states that the proportion of primes ending in a certain digit (or having a certain residue) approaches 1/φ(n) as the size of the numbers considered grows, where φ(n) is Euler's totient function.
What is Euler's totient function, and how does it relate to the distribution of prime numbers?
-Euler's totient function, denoted by φ(n), counts the number of integers up to n that are co-prime (or relatively prime) to n. It is crucial in understanding the distribution of prime numbers because it helps determine the expected density of primes within different residue classes mod n, as described by Dirichlet's theorem.
What is the significance of the number 710 in the script?
-The number 710 is significant because it is a rational approximation for 2π, and it is used to illustrate the concept of residue classes mod 710. When points are plotted with steps of 710 radians, they form nearly straight lines, which is a visual demonstration of the close approximation to a full turn of 2π radians.
How does the script explain the missing 'teeth' in the comb-like pattern observed in the polar plot of prime numbers?
-The missing 'teeth' in the comb-like pattern are explained by the fact that certain residue classes mod 44 (and by extension mod 710) do not contain any prime numbers. These classes are those that are divisible by the factors of 44 (1, 2, 4, 11, 22, and 44), and thus no prime numbers can appear in these classes based on divisibility rules.
What is the role of complex analysis in the study of prime numbers and their distribution?
-Complex analysis, the study of functions with complex numbers as inputs and outputs, plays a crucial role in the study of prime numbers and their distribution. It is a foundational tool in modern analytic number theory and has been instrumental in proving deep theorems like Dirichlet's theorem, as well as in recent research on the distribution of primes.
How does the script's exploration of prime numbers in polar coordinates relate to the broader theme of discovering important mathematical concepts?
-The script demonstrates that even seemingly arbitrary explorations of numbers can lead to important and deep mathematical insights. By following a line of inquiry sparked by a visual pattern, one can stumble upon significant theorems and concepts, such as Dirichlet's theorem, which is a central result in number theory.
What is the significance of the number 44 in the context of the script?
-The number 44 is significant because it is used to illustrate the concept of residue classes mod 44. The script explains that 44 steps in the polar plot correspond to almost 7 full turns (since 44 is close to 7 times 2π), leading to the formation of spirals and the demonstration of how primes are distributed across these residue classes.
How does the script use the concept of 'residue class mod n' to explain the patterns observed in the polar plot?
-The script uses the concept of 'residue class mod n' to explain the patterns by showing how numbers that are a certain distance from multiples of n (in this case, 6, 44, and 710) form spirals or lines in the polar plot. This concept helps to understand the distribution of primes and other numbers across different angles and distances from the origin.
Outlines
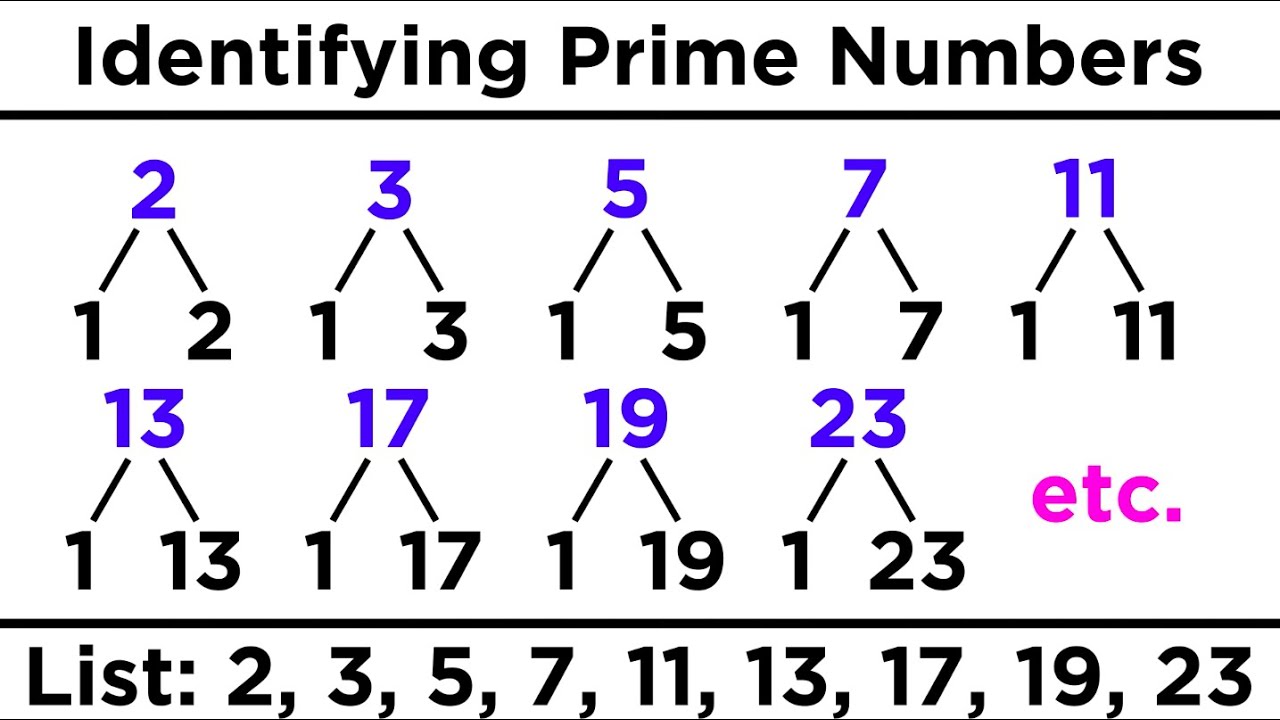
📊 Exploring Prime Numbers and Polar Coordinates
The paragraph begins with a discussion on a pattern observed in polar coordinates related to prime numbers and pi, as seen on Math Stack Exchange. It introduces the concept of polar coordinates, contrasting it with the usual Cartesian coordinates, and explains how points in 2D space are labeled with a radius and an angle (theta) measured in radians. The pattern involves plotting points where both coordinates are prime numbers, which leads to a visualization of spirals and rays when zoomed out. The paragraph also touches on the distribution of primes and the transition from chaotic spirals to orderly rays at larger scales, hinting at deeper mathematical principles.
🔄 Understanding the Spirals and Residue Classes
This paragraph delves into the explanation of the spiral patterns observed in the previous section. It describes how counting by 6 leads to almost full turns, creating the illusion of a single curving line. The paragraph clarifies that prime numbers cannot be multiples of 6, which explains the absence of certain spiral arms when focusing on primes. It introduces the concept of residue classes mod 6 and explains how these sequences relate to the observed spirals. The paragraph also sets up the groundwork for understanding larger patterns by discussing the relationship between the number of steps (44 in this case) and the close approximation to full turns, leading to the concept of residue classes mod 44.
🌌 The Milky Way of Prime Numbers
The paragraph continues the exploration of prime numbers in polar coordinates, focusing on the larger scale and the appearance of Milky Way-like gaps. It explains how the primes are distributed among the residue classes mod 44 and how this leads to the observed pattern of gaps and clumps. The paragraph introduces the concept of relatively prime numbers, also known as co-prime, and Euler's totient function, which counts the number of co-prime integers up to a given number. It also discusses the significance of 710 radians being a close approximation to a full turn and how this leads to the formation of nearly straight lines in the visualization.
📈 Patterns in Prime Distribution
This paragraph discusses the distribution of prime numbers among residue classes mod 10 and mod 44, using histograms to illustrate the even spread of primes across these classes. It challenges the expectation of an even distribution and highlights the non-obvious nature of proving such a pattern. The paragraph introduces Dirichlet's theorem, which states that the primes are equally dense in any residue class that is co-prime to the divisor, and explains its significance in number theory. It also touches on the complexity of proving this theorem and its reliance on complex analysis, emphasizing the relevance of understanding prime distribution in modern mathematical research.
🎯 The Value of Serendipitous Mathematical Exploration
The final paragraph reflects on the value of exploring mathematics through data visualization and serendipitous discovery. It emphasizes that even arbitrary explorations can lead to important and deep mathematical facts, such as Dirichlet's theorem. The paragraph argues that this kind of exploration can make mathematical concepts more familiar and easier to understand when formally introduced. It concludes by encouraging the pursuit of mathematical curiosity and the joy of rediscovery, which can lead to a more effective learning experience.
Mindmap
Keywords
💡Polar Coordinates
💡Archimedean Spiral
💡Prime Numbers
💡Residue Class
💡Dirichlet's Theorem
💡Euler's Totient Function
💡Rational Approximations for Pi
💡Complex Analysis
💡Data Visualization
💡Number Theory
Highlights
The discussion revolves around the distribution of prime numbers and their relationship with rational approximations for pi.
The user's exploration began with playing around with data in polar coordinates, which labels points based on distance from the origin (radius) and the angle with the horizontal (theta).
Polar coordinates are not unique as adding 2 pi to the angle coordinate doesn't change the location.
The pattern observed involves plotting points where both coordinates are a given prime number, leading to a visualization known as an Archimedean spiral.
When zooming out, the seemingly random distribution of primes in polar coordinates reveals clear, galactic-seeming spirals.
The spirals, upon further zooming, give way to different patterns of outward-pointing rays, some in clumps of four with occasional gaps.
The number of spirals (20) and rays (280) raises questions about their origins and why they arise from primes.
The initial exploration with prime numbers might be misleading; similar spirals are seen with all whole numbers, not just primes.
The spirals' origin is not related to primes but is satisfactorily explained by residue classes mod 6.
Prime numbers cannot be multiples of 6, which explains why most spiral arms disappear when filtering for primes.
The concept of residue classes mod 6 is introduced, relating to counting up by 6 and the resulting almost full turns.
The pattern observed at a larger scale is related to 44 steps being very close to a whole number of turns, leading to residue classes mod 44.
Primes are distributed among residue classes mod 44 in a seemingly random fashion, illustrating a deep fact in number theory.
The primes' distribution among residue classes is explained by Euler's totient function, which counts numbers co-prime to a given number.
The discussion ties the observed patterns to Dirichlet's theorem, a fundamental theorem in number theory about the distribution of primes.
Dirichlet's theorem states that the primes are just as dense in any one residue class as in any other, leading to an even spread of primes among the classes.
The proof of Dirichlet's theorem relies on complex analysis, showing a connection between primes and continuous functions.
Understanding the distribution of primes in residue classes is still relevant in modern research, including breakthroughs on the twin-prime conjecture.
The importance of exploring numbers arbitrarily, as it can lead to meaningful discoveries and a deeper understanding of mathematical concepts.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: