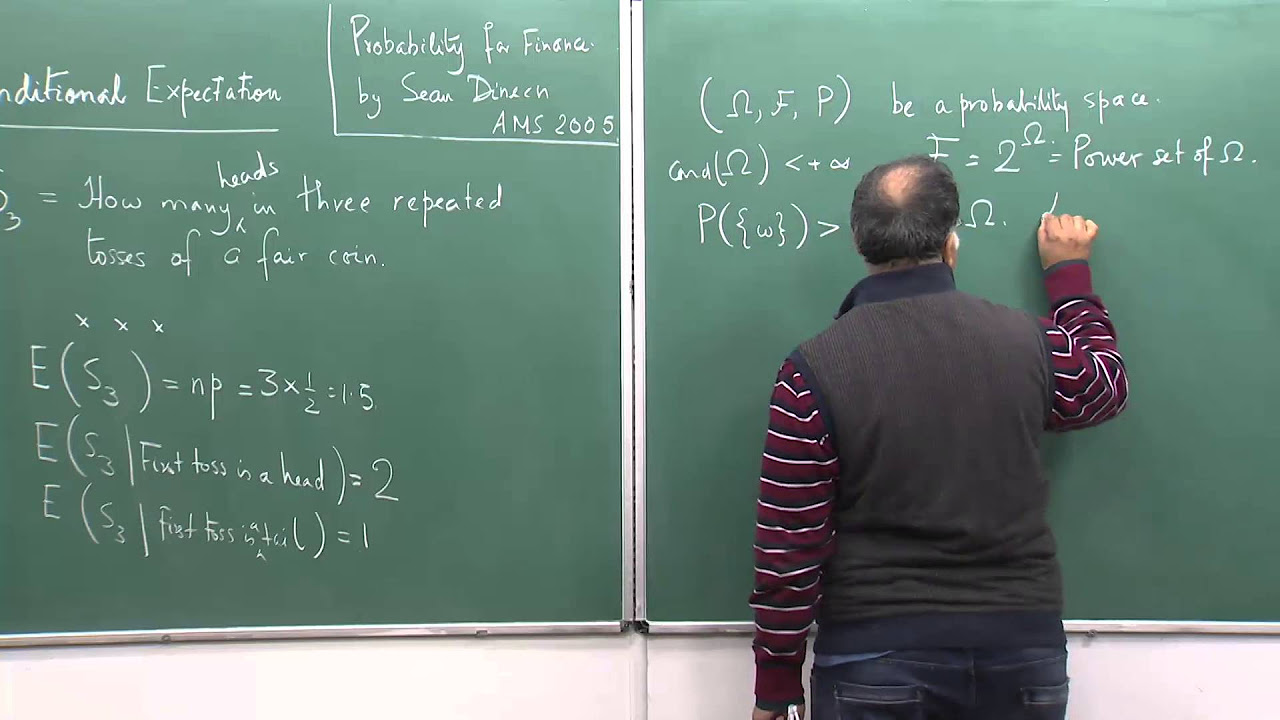Lecture 1: Basic Probability
TLDRThis course on probability and stochastics for finance begins by emphasizing the misconceptions about easy money in financial markets, highlighting the importance of understanding uncertainty. It delves into the fundamentals of probability as a measure of randomness, tracing its origins to gambling problems and the collaboration between Pascal and Fermat. The instructor outlines the limitations of classical probability definitions and introduces Kolmogorov's axiomatic approach suitable for both finite and infinite sample spaces, setting a foundation for analyzing financial products and markets.
Takeaways
- 🎓 The course aims to teach probability and stochastics with a focus on their application in finance, emphasizing that understanding these concepts is crucial for navigating the complexities of financial markets.
- 💰 The instructor challenges the common notion that making money in the financial market is easy, highlighting that the market is filled with uncertainties and success stories like Warren Buffet are exceptions.
- 📈 The importance of knowing the 'language of uncertainty' is underscored, which refers to the mathematical tools from probability and stochastics needed to analyze financial markets.
- 🚫 A clear warning is given that without understanding probability, one cannot truly comprehend financial products, their pricing, or the market itself.
- 🔑 The concept of randomness is introduced as a lack of prior knowledge about the outcome of an activity, using the example of tossing a coin to illustrate the idea.
- 🎲 The origins of probability theory are traced back to gambling problems, with a specific mention of the French gambler Chevalier de Mere and his question to mathematician Blaise Pascal.
- 📚 The script discusses the evolution of probability from a simple understanding to a formal mathematical theory, initiated by the correspondence between Pascal and Fermat.
- 🔍 The notion of a random experiment is explained, defining it as an experiment with an unknown outcome, and its relevance to financial markets, such as the unpredictable stock prices, is highlighted.
- 🌐 The script introduces the concept of a sample space, which is the set of all possible outcomes of a random experiment, and the assumption that these outcomes are known, finite, or infinite.
- 📉 The limitations of the classical definition of probability are discussed, pointing out its circular logic and inability to handle infinite sample spaces.
- 📘 Kolmogorov's axioms of probability are introduced as the foundation for a rigorous understanding of probability, applicable to both finite and infinite sample spaces.
Q & A
What is the main theme of this course on probability and stochastics for finance?
-The main theme of the course is to understand the language of uncertainty in finance through the study of probability and stochastics, which are essential for comprehending the financial market and pricing financial commodities.
Why does the instructor suggest that making money in the financial market is not easy?
-The instructor suggests that making money in the financial market is not easy because it is filled with uncertainties, and without understanding the language of uncertainty, one cannot have a better understanding of the financial market and is exposed to investment risks.
What is randomness in the context of this course?
-In the context of this course, randomness refers to the lack of prior knowledge about the outcome of a certain activity, such as not knowing whether a tossed coin will land on heads or tails.
How did the mathematical ideas of probability originate?
-The mathematical ideas of probability originated from looking at problems of gambling, with the famous French gambler Chevalier de Mere posing a question to mathematician Blaise Pascal, which led to the development of modern probability theory with the help of Pierre de Fermat.
What is a random experiment according to the script?
-A random experiment is an experiment whose outcome is not known to us, such as throwing a die, tossing a coin, or the uncertainty of stock prices in the market.
What is the basic assumption when considering all possible outcomes of a random experiment?
-The basic assumption is that all possible outcomes of a random experiment are known, which could be finite or infinite, and this assumption is necessary for the science of probability to proceed.
Why is the traditional definition of probability flawed when dealing with infinite sample spaces?
-The traditional definition of probability is flawed when dealing with infinite sample spaces because it assumes outcomes are mutually exclusive, exhaustive, and equally likely, which is not applicable in cases where the sample space is infinite.
Outlines
📈 Introduction to Probability and Finance
The instructor begins the course by addressing the common misconception that finance is easy, emphasizing the importance of understanding uncertainty in financial markets. They introduce the course's two-part structure, focusing first on probability and stochastics, then on financial commodity pricing. The necessity of grasping the language of uncertainty through probability theory is highlighted, as is the difficulty of defining randomness and the historical connection between probability theory and gambling, exemplified by the collaboration between Blaise Pascal and Pierre de Fermat.
🎲 Understanding Randomness and Random Experiments
This paragraph delves into the concept of randomness, defining it as the lack of prior knowledge of outcomes from certain activities. The instructor uses the example of dice throws to illustrate randomness and discusses the development of probability theory from gambling problems. The notion of a random experiment is introduced, with examples such as stock prices and car accidents, to emphasize the unpredictability of outcomes. The instructor also touches on Bayesian ideas and the importance of defining a sample space for probability discussions.
📚 The Foundations of Probability Theory
The paragraph discusses the basic assumptions of probability, such as knowing all possible outcomes of a random experiment, which could be finite or infinite. It contrasts the classical definition of probability, which is based on equally likely outcomes, with the need for an axiomatic approach to handle more complex scenarios, including infinite sample spaces. The instructor introduces the concept of a sample space and the limitations of the classical definition, pointing out its circular logic and inability to address certain cases.
🔢 Critique of Classical Probability and Introduction to Axiomatic Formalism
The instructor critiques the classical definition of probability for its circular reasoning and its limitations in handling infinite sample spaces. They introduce the axiomatic formalism of probability developed by Kolmogorov, emphasizing the need to move beyond basic intuitions to a more rigorous mathematical framework. The paragraph sets the stage for a deeper exploration of probability in the context of both finite and infinite sample spaces, hinting at the paradoxes that can arise without a formal approach.
📐 Kolmogorov's Axioms of Probability
This paragraph presents Kolmogorov's axioms as the foundation for a formal understanding of probability. The instructor outlines the conditions that define a probability space, including the sample space, the sigma-algebra of events, and the probability measure itself. They explain the axioms that any probability measure must satisfy, such as the assignment of values between 0 and 1, the inclusion of the empty set and the entire sample space, and the rules governing the probability of unions of events.
🔑 The Utility of Axiomatic Probability in Finite and Infinite Sample Spaces
The instructor discusses the practicality of Kolmogorov's axioms in both finite and infinite sample spaces. They highlight the importance of the sigma-algebra in defining events and the limitations of the classical definition when dealing with infinite outcomes. The paragraph also foreshadows the discussion of the Bertrand paradox and other historical problems in the next class, emphasizing the utility of the axiomatic approach in resolving such paradoxes and in constructing probability spaces.
🚀 Conclusion and Preview of Upcoming Lectures
In conclusion, the instructor summarizes the importance of the axiomatic approach to probability and its applicability to various sample spaces. They provide a preview of the next lecture, which will include problem-solving related to the Bertrand paradox, Buffon's needle problem, and the construction of probability spaces.
Mindmap
Keywords
💡Probability
💡Stochastics
💡Financial Market
💡Uncertainty
💡Randomness
💡Binomial Theorem
💡Sample Space
💡Mutually Exclusive
💡Axiomatic Formalism
💡Kolmogorov's Axioms
💡Sigma-Algebra
Highlights
Introduction to the course on probability and stochastics for finance, emphasizing the importance of understanding uncertainty in financial markets.
The challenge of making easy money in financial markets, highlighting the exceptions like Warren Buffet and the inherent risks.
The necessity of knowing the language of uncertainty through probability and stochastics to succeed in finance.
The two-part course structure: the first on probability and stochastics, and the second on financial commodities pricing.
Definition of probability as a tool to understand randomness, with examples like coin tosses and dice throws.
Historical origins of probability theory in gambling problems, involving Chevalier de Mere and Blaise Pascal.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: